A vessel contains water up to a height of 20 cm and above it an oil up to another 20 cm. The refractive indices of the water and the oil are 1.33 and F30 respectively. Find the apparent depth of the vessel when viewed from above.
The correct Answer is:C, D
To find the apparent depth of the vessel containing water and oil, we will follow these steps:
Step 1: Understand the Setup
We have a vessel with two layers:
- Water with a height of 20 cm and a refractive index (μ_w) of 1.33.
- Oil with a height of 20 cm and a refractive index (μ_o) of 1.30.
Step 2: Calculate the Total Real Depth
The total real depth (D) of the liquid column is the sum of the depths of water and oil:
D=Depth of Water+Depth of Oil=20cm+20cm=40cm
Step 3: Calculate the Shift Due to Water
The shift in depth due to the water layer can be calculated using the formula:
Shift due to Water=(1−1μw)×Thickness of Water
Substituting the values:
Shift due to Water=(1−11.33)×20cm
Calculating:
Shift due to Water=(1−0.7519)×20≈0.2481×20≈4.962cm≈5cm
Step 4: Calculate the Shift Due to Oil
Now, we calculate the shift in depth due to the oil layer using the same formula:
Shift due to Oil=(1−1μo)×Thickness of Oil
Substituting the values:
Shift due to Oil=(1−11.30)×20cm
Calculating:
Shift due to Oil=(1−0.7692)×20≈0.2308×20≈4.616cm≈4.6cm
Step 5: Calculate the Total Shift
Now, we add the shifts due to both layers:
Total Shift=Shift due to Water+Shift due to Oil
Substituting the values:
Total Shift=5cm+4.6cm=9.6cm
Step 6: Calculate the Apparent Depth
Finally, the apparent depth (D_a) can be calculated by subtracting the total shift from the total real depth:
Da=D−Total Shift
Substituting the values:
Da=40cm−9.6cm=30.4cm
Final Answer
The apparent depth of the vessel when viewed from above is 30.4 cm.
---
We have a vessel with two layers:
- Water with a height of 20 cm and a refractive index (μ_w) of 1.33.
- Oil with a height of 20 cm and a refractive index (μ_o) of 1.30.
The total real depth (D) of the liquid column is the sum of the depths of water and oil:
D=Depth of Water+Depth of Oil=20cm+20cm=40cm
The shift in depth due to the water layer can be calculated using the formula:
Shift due to Water=(1−1μw)×Thickness of Water
Substituting the values:
Shift due to Water=(1−11.33)×20cm
Calculating:
Shift due to Water=(1−0.7519)×20≈0.2481×20≈4.962cm≈5cm
Now, we calculate the shift in depth due to the oil layer using the same formula:
Shift due to Oil=(1−1μo)×Thickness of Oil
Substituting the values:
Shift due to Oil=(1−11.30)×20cm
Calculating:
Shift due to Oil=(1−0.7692)×20≈0.2308×20≈4.616cm≈4.6cm
Now, we add the shifts due to both layers:
Total Shift=Shift due to Water+Shift due to Oil
Substituting the values:
Total Shift=5cm+4.6cm=9.6cm
Finally, the apparent depth (D_a) can be calculated by subtracting the total shift from the total real depth:
Da=D−Total Shift
Substituting the values:
Da=40cm−9.6cm=30.4cm
The apparent depth of the vessel when viewed from above is 30.4 cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE
9 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
Three immiscibles transparent liquids with erefractive indices 3/2,4/3 and 6/5 are arranged one on top of another. The depth of the liquid are 3 cm, 4 cm and 6 cm respectively. The apparent depth of the vessel is
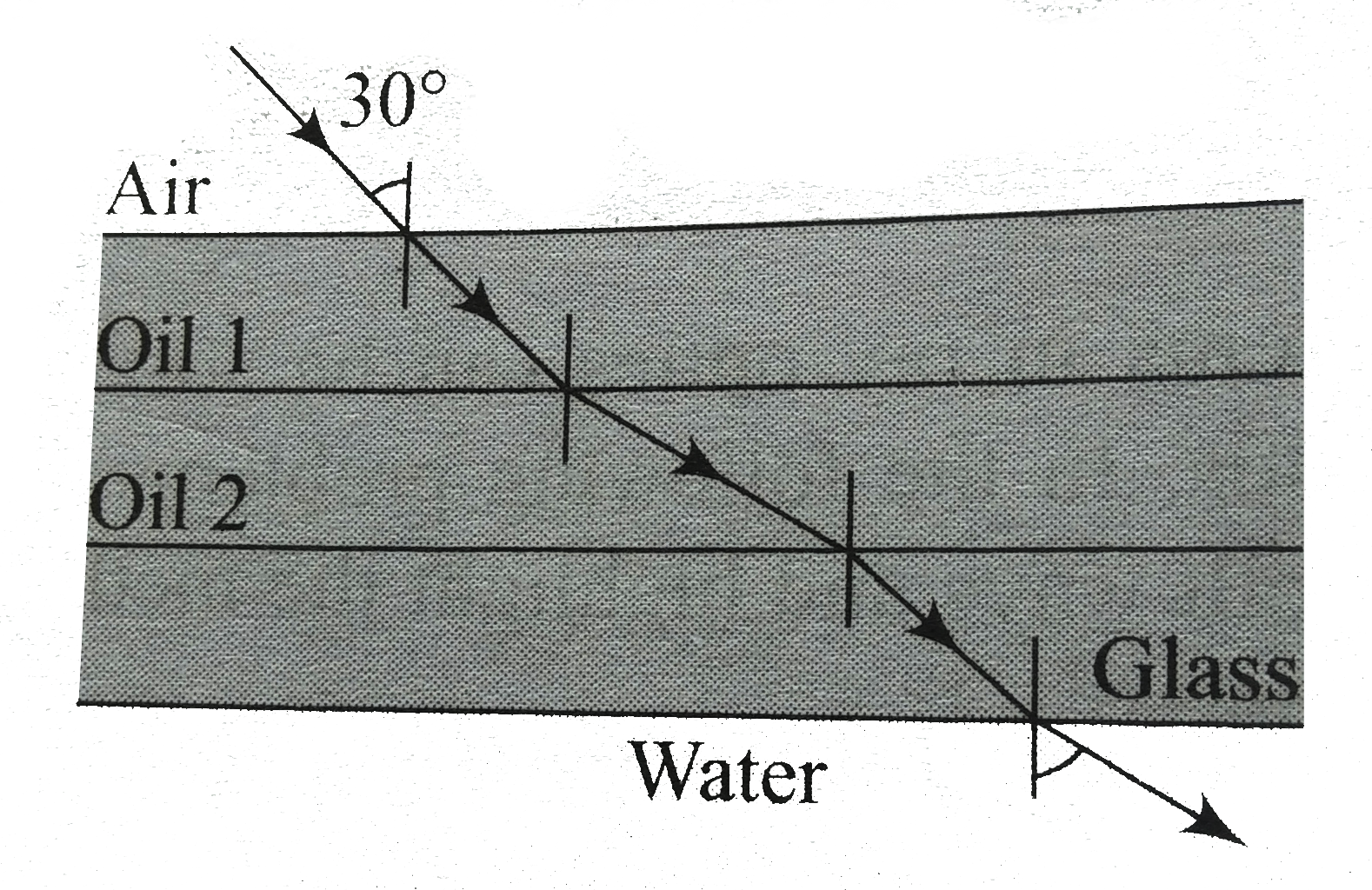
View SolutionLight is incident from air on an oil layer at an incident angle of 30∘. After moving through the oil 1, oil 2, and glass it enters water. If the refraction index of glass and water are 1.5 and 1.3, respectively. Find the angle which the ray makes with the normal in water.
View Solution
Knowledge Check
A vesse of depth x is half filled with oil of refractive index μ1 and the other half is filled with water of refrative index μ2. The apparent depth of the vessel when viewed above is
Ax(μ1+μ2)2μ1μ2Bxμ1μ22(μ1+μ2)Cxμ1μ2(μ1+μ2)D2x(μ1+μ2)μ1μ2
A beaker contains water up to a height h1 and K oil above water up to another height h2. Find the apparent shift in the position of the bottom of the beaker when viewed from above. Refractive index of water is μ1 and that of K.oil is mu_2.
View SolutionA container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water =4/3.
View SolutionThe apparent depth of a liquid in a vessel is 15 cm, when its real depth is 20 cm. find the refractive index of the liquid.
View SolutionA container open at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 14 cm with radii of its lower and upper circular ends as 8 cm and 20 cm, respectively. find the capacity of the container.
View SolutionA vessel contains water up to a height of 1.5 m. Taking the density of water 103kg m−3 , acceleration due to gravity 9.8m s−2 and area of base of vessel 100cm2, calculate the pressure
View SolutionA vessel in the form of a hemisphereical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are respectively 6cm and 4cm. Find the height of water in the cylinder.
View SolutionA vessel in the form of a hemisphereical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are respectively 6cm and 4cm. Find the height of water in the cylinder.
View Solution
