A large plane sheet of charge having surface charge density 5×10−16cm−2 lies in XY plane. Find electric flux through a circular area of radius 1cm Given normal to the circular area makes an angle of 60∘ with Z-axis.
To solve the problem step by step, we will follow the outlined procedure based on the information given in the question.
Step 1: Identify the Given Values
- Surface charge density, σ=5×10−16C/m2
- Radius of the circular area, R=1cm=1×10−2m
- Angle between the normal to the circular area and the z-axis, θ=60∘
- Value of ϵ0=8.85×10−12C2/N m2
Step 2: Calculate the Electric Field due to the Plane Sheet
The electric field E due to an infinite plane sheet of charge is given by the formula:
E=σ2ϵ0
Substituting the values:
E=5×10−162×8.85×10−12
Step 3: Calculate the Area of the Circular Region
The area S of the circular region is given by:
S=πR2
Substituting the radius:
S=π(1×10−2)2=π×10−4m2
Step 4: Calculate the Electric Flux
The electric flux Φ through the circular area is given by:
Φ=E⋅S⋅cosθ
Substituting the values we have:
Φ=E⋅π×10−4⋅cos(60∘)
Since cos(60∘)=12:
Φ=E⋅π×10−4⋅12
Step 5: Substitute the Electric Field and Calculate Flux
Now substituting E from Step 2 into the flux equation:
Φ=(5×10−162×8.85×10−12)⋅π×10−4⋅12
Calculating this step by step:
1. Calculate E:
E=5×10−162×8.85×10−12≈2.83×10−5N/C
2. Calculate Φ:
Φ=(2.83×10−5)⋅(π×10−4)⋅12
Φ≈2.83×10−5⋅1.57×10−4⋅12≈2.22×10−9N m2/C
Final Answer
The electric flux through the circular area is approximately:
Φ≈4.43×10−9N m2/C
- Surface charge density, σ=5×10−16C/m2
- Radius of the circular area, R=1cm=1×10−2m
- Angle between the normal to the circular area and the z-axis, θ=60∘
- Value of ϵ0=8.85×10−12C2/N m2
The electric field E due to an infinite plane sheet of charge is given by the formula:
E=σ2ϵ0
Substituting the values:
E=5×10−162×8.85×10−12
The area S of the circular region is given by:
S=πR2
Substituting the radius:
S=π(1×10−2)2=π×10−4m2
The electric flux Φ through the circular area is given by:
Φ=E⋅S⋅cosθ
Substituting the values we have:
Φ=E⋅π×10−4⋅cos(60∘)
Since cos(60∘)=12:
Φ=E⋅π×10−4⋅12
Now substituting E from Step 2 into the flux equation:
Φ=(5×10−162×8.85×10−12)⋅π×10−4⋅12
Calculating this step by step:
1. Calculate E:
E=5×10−162×8.85×10−12≈2.83×10−5N/C
2. Calculate Φ:
Φ=(2.83×10−5)⋅(π×10−4)⋅12
Φ≈2.83×10−5⋅1.57×10−4⋅12≈2.22×10−9N m2/C
The electric flux through the circular area is approximately:
Φ≈4.43×10−9N m2/C
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 5
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 6
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A large plane charge sheet having surface xharge density σ=2.0×10−6Cm−2 lies in the x-y plane. Find the flux of the electric field through a circular area of radius 1 cm lying completely in the region where x, y, z are all positive and with its normal making an angle of 600 with the z-axis.
View SolutionA large conducting plane has a surface charge density 1.0x10−4Cm−2 . Find the electrostatic energy stored in a cubical volume of edge 1 cm in the front plane.
View SolutionAn infinite thin plane sheet of charge density 7.08×10−11(C/m2) is held in air. Find the electric field at a point very close to the sheet.
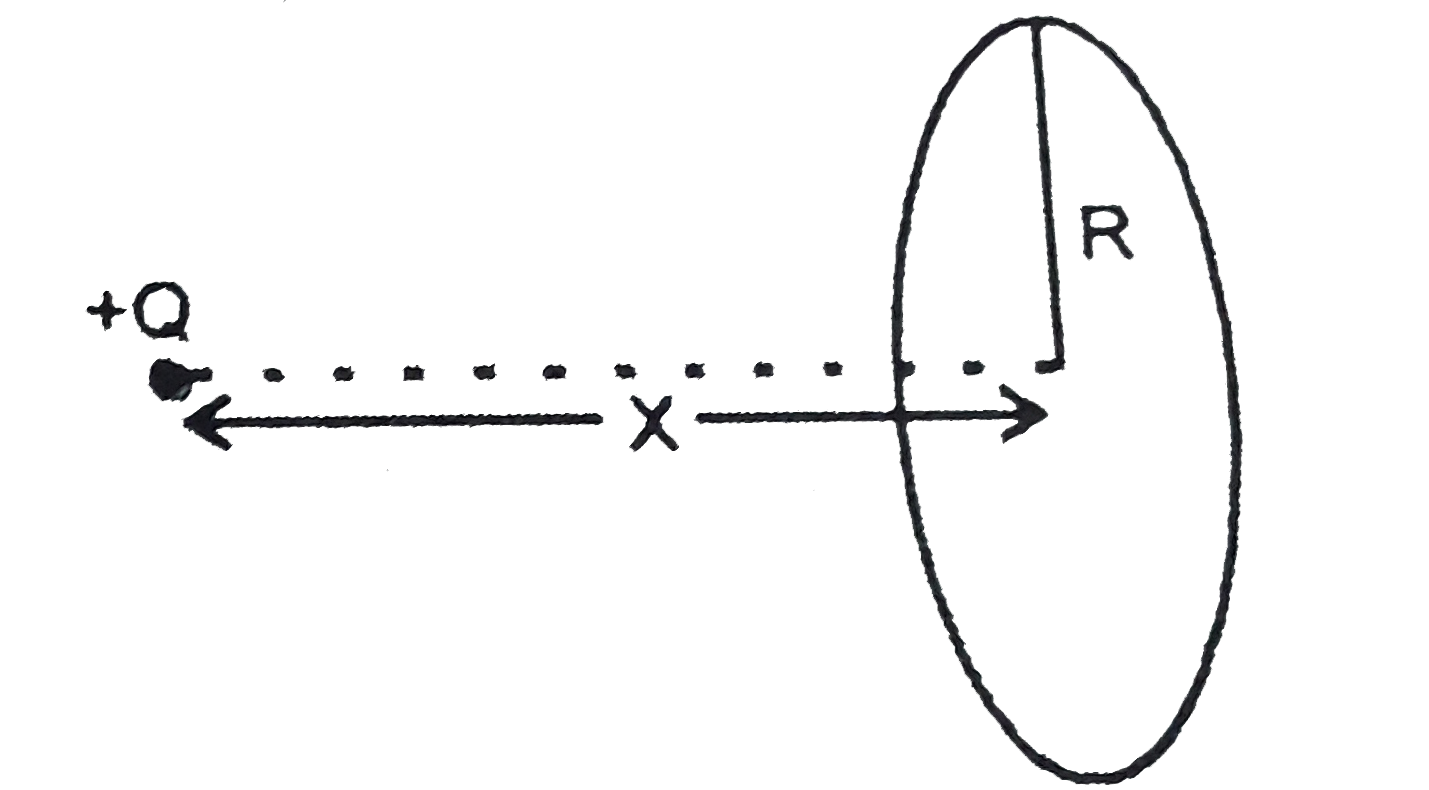
View SolutionFind the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
View SolutionA charge of 8.85C is placed at the centre of a spherical Guassian surface of radius 5cm. The electric flux through the surface is
View SolutionA 2A current is flowing through a circular coil of radius 10 cm containing 100 turns. Find the magnetic flux density at the centre of the coil.
View SolutionConsider →E=3×103ˆi(N/C) then what is the flux through the square of 10cm side, if the normal of its plane makes 60∘ angle with the X axis.
View SolutionA point charge q is placed at origin. Find the flux of electric,produced due to this charge, through a circle of radius R lying in y-z plane. The centre of the circle lies at (x,0).
View SolutionTwo parallel large thin metal sheets have equal surface charge densities (σ=26.4×10−12C/m2) of opposite signs. The electric field between these sheets is
View SolutionConsider a uniform electric field E=3×103ˆiN/C. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane ? (b) What is the flux through the same square if the normal to its plane makes a 60∘ angle with the x-axis ?
View Solution
