The temperature (T) dependence of resistivity (rho) of a semiconductor is represented by :
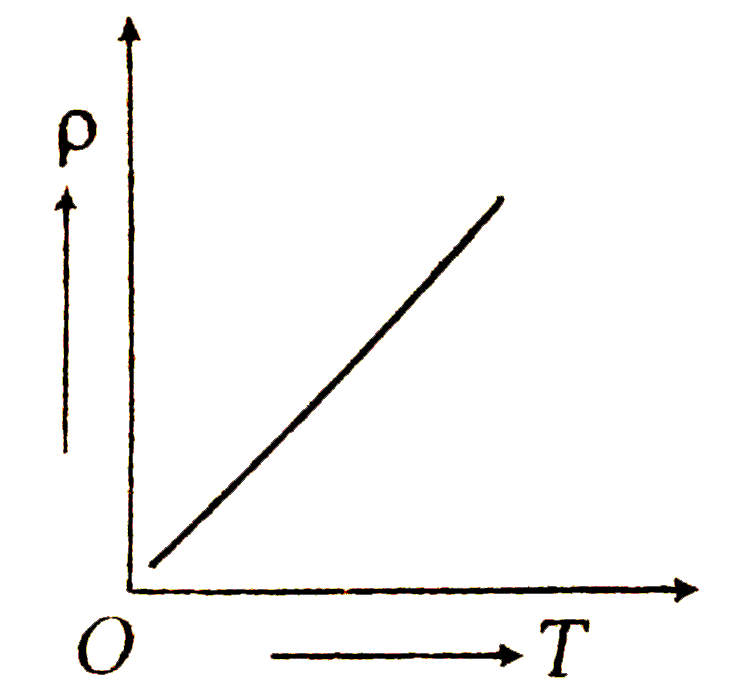

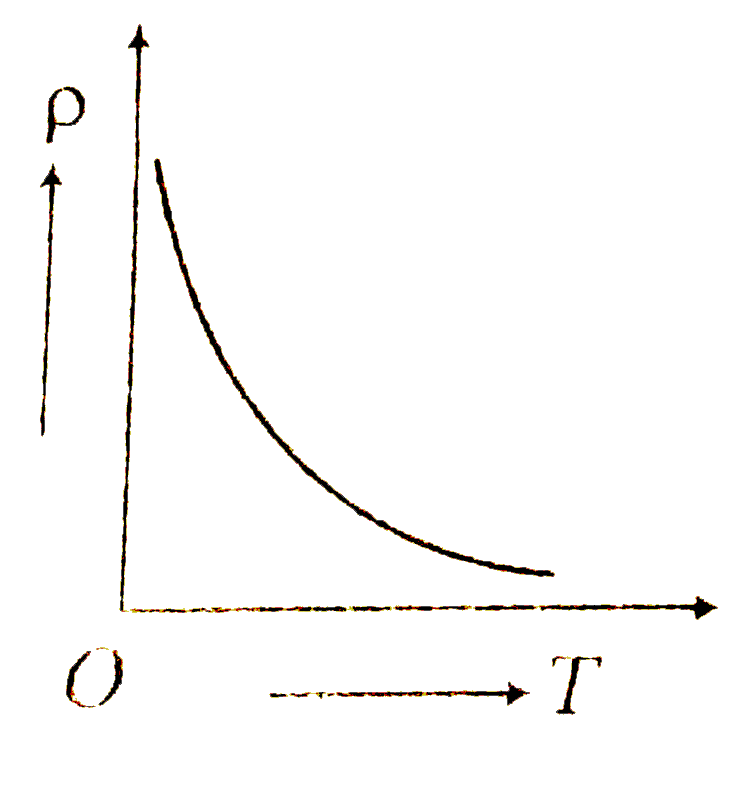
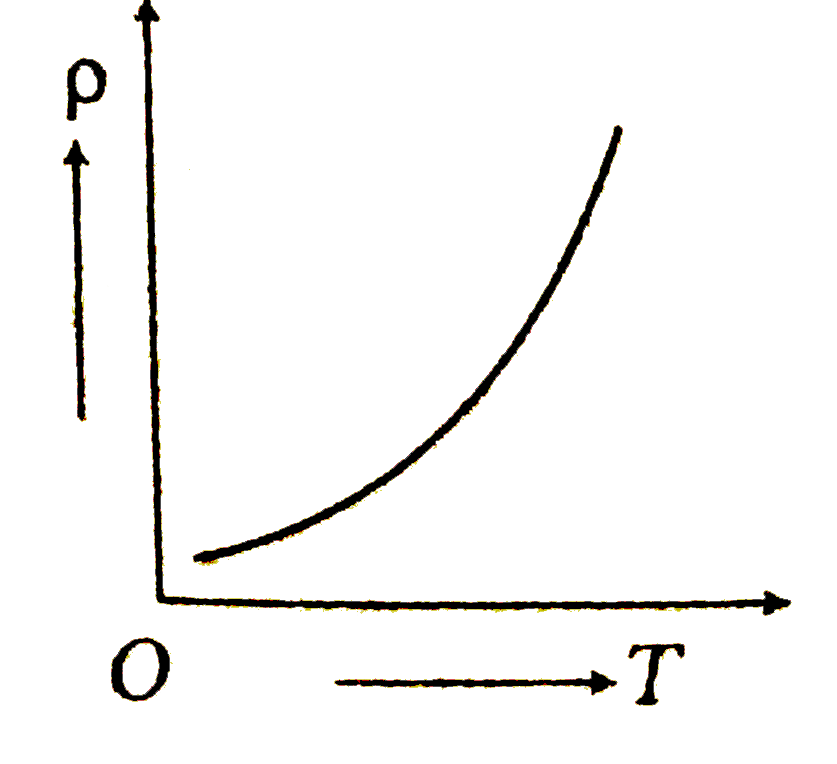
The correct Answer is:C
To understand the temperature dependence of resistivity (ρ) of a semiconductor, we can break down the problem step by step.
1. Understanding Resistivity and Temperature:
The resistivity of a semiconductor changes with temperature. The relationship can be expressed as:
Δρ=ρ0αΔT
where:
- Δρ is the change in resistivity,
- ρ0 is the initial resistivity,
- α is the temperature coefficient of resistivity,
- ΔT is the change in temperature.
2. Expressing the Change in Resistivity:
We can express the change in resistivity in terms of initial and final temperatures:
Δρ=ρ(T)−ρ0=ρ0α(T−T0)
Rearranging gives:
ρ(T)=ρ0+ρ0α(T−T0)
3. Identifying the Linear Relationship:
The equation can be rewritten as:
ρ(T)=ρ0(1+α(T−T0))
This shows that resistivity is a linear function of temperature, where:
- The slope of the line is ρ0α,
- The y-intercept is ρ0.
4. Sign of the Temperature Coefficient:
For semiconductors, the temperature coefficient α is typically negative. This means that as the temperature increases, the resistivity decreases, leading to a negative slope in the graph of resistivity versus temperature.
5. Graphical Representation:
Since α is negative, the graph of ρ versus T will have a negative slope. This indicates that the resistivity decreases with an increase in temperature.
6. Conclusion:
Based on the analysis, the correct representation of the temperature dependence of resistivity for a semiconductor will show a downward slope in the graph.
Final Answer:
The correct option for the temperature dependence of resistivity of a semiconductor is the one that shows a negative slope.
The resistivity of a semiconductor changes with temperature. The relationship can be expressed as:
Δρ=ρ0αΔT
where:
- Δρ is the change in resistivity,
- ρ0 is the initial resistivity,
- α is the temperature coefficient of resistivity,
- ΔT is the change in temperature.
We can express the change in resistivity in terms of initial and final temperatures:
Δρ=ρ(T)−ρ0=ρ0α(T−T0)
Rearranging gives:
ρ(T)=ρ0+ρ0α(T−T0)
The equation can be rewritten as:
ρ(T)=ρ0(1+α(T−T0))
This shows that resistivity is a linear function of temperature, where:
- The slope of the line is ρ0α,
- The y-intercept is ρ0.
For semiconductors, the temperature coefficient α is typically negative. This means that as the temperature increases, the resistivity decreases, leading to a negative slope in the graph of resistivity versus temperature.
Since α is negative, the graph of ρ versus T will have a negative slope. This indicates that the resistivity decreases with an increase in temperature.
Based on the analysis, the correct representation of the temperature dependence of resistivity for a semiconductor will show a downward slope in the graph.
The correct option for the temperature dependence of resistivity of a semiconductor is the one that shows a negative slope.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Resistivity of a semiconductor depends on
View SolutionTemperature dependence of resistivity p(T) of semiconductors, insulators and metals is significantly based on the following factors:
View SolutionThe electrical resistivity of a semiconductor :
View SolutionThe conductivity of a semiconductor depends upon
View SolutionState the order of specific resistance of
a semiconductor
View SolutionThe temperature dependence of resistance of Cu and undoped Si in the temperature range 300−400K, is best described by :
View SolutionTemperature dependence of drift velocity depends on the following factors.
View SolutionBy increasing the temperature , the specific resistance of a conductor and a semiconductor
View SolutionHow does an increase in the temperature affect the specific resistance of a :
Semiconductor ?
View SolutionHow does the conductivity of a semiconductor change if its temperature is raised ?
View Solution