Two resistance wires on joining in parallel the resultant resistance is ohms 65 ohms. One of the wire breaks, the effective resistance is 2 ohms . The resistance of the broken wire is
35Ω
2Ω
65Ω
3Ω
The correct Answer is:D
To solve the problem, we need to find the resistance of the broken wire given the conditions of the circuit. Let's denote the two resistances as R1 and R2.
Step 1: Write the formula for equivalent resistance in parallel
The formula for the equivalent resistance R of two resistors R1 and R2 connected in parallel is given by:
1R=1R1+1R2
Given that the resultant resistance when both wires are connected in parallel is 65 ohms, we can write:
165=1R1+1R2
This simplifies to:
56=1R1+1R2
Step 2: Rearranging the equation
Rearranging the equation gives:
1R1+1R2=56
Multiplying through by R1R2 gives:
R2+R1=56R1R2
Step 3: Consider the case when one wire breaks
When one of the wires breaks, let's assume R1 breaks. The effective resistance then becomes R2, which is given as 2 ohms. Therefore:
R2=2 ohms
Step 4: Substitute R2 back into the equation
Substituting R2=2 into the earlier equation:
2+R1=56R1⋅2
This simplifies to:
2+R1=106R1
or
2+R1=53R1
Step 5: Solve for R1
Now, rearranging gives:
2=53R1−R1
This can be rewritten as:
2=(53−33)R1
2=23R1
Multiplying both sides by 32:
R1=3 ohms
Conclusion
Thus, the resistance of the broken wire R1 is 3 ohms.
---
The formula for the equivalent resistance R of two resistors R1 and R2 connected in parallel is given by:
1R=1R1+1R2
Given that the resultant resistance when both wires are connected in parallel is 65 ohms, we can write:
165=1R1+1R2
This simplifies to:
56=1R1+1R2
Rearranging the equation gives:
1R1+1R2=56
Multiplying through by R1R2 gives:
R2+R1=56R1R2
When one of the wires breaks, let's assume R1 breaks. The effective resistance then becomes R2, which is given as 2 ohms. Therefore:
R2=2 ohms
Substituting R2=2 into the earlier equation:
2+R1=56R1⋅2
This simplifies to:
2+R1=106R1
or
2+R1=53R1
Now, rearranging gives:
2=53R1−R1
This can be rewritten as:
2=(53−33)R1
2=23R1
Multiplying both sides by 32:
R1=3 ohms
Thus, the resistance of the broken wire R1 is 3 ohms.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Knowledge Check
Equivalent resistance (in ohm) of the given network is
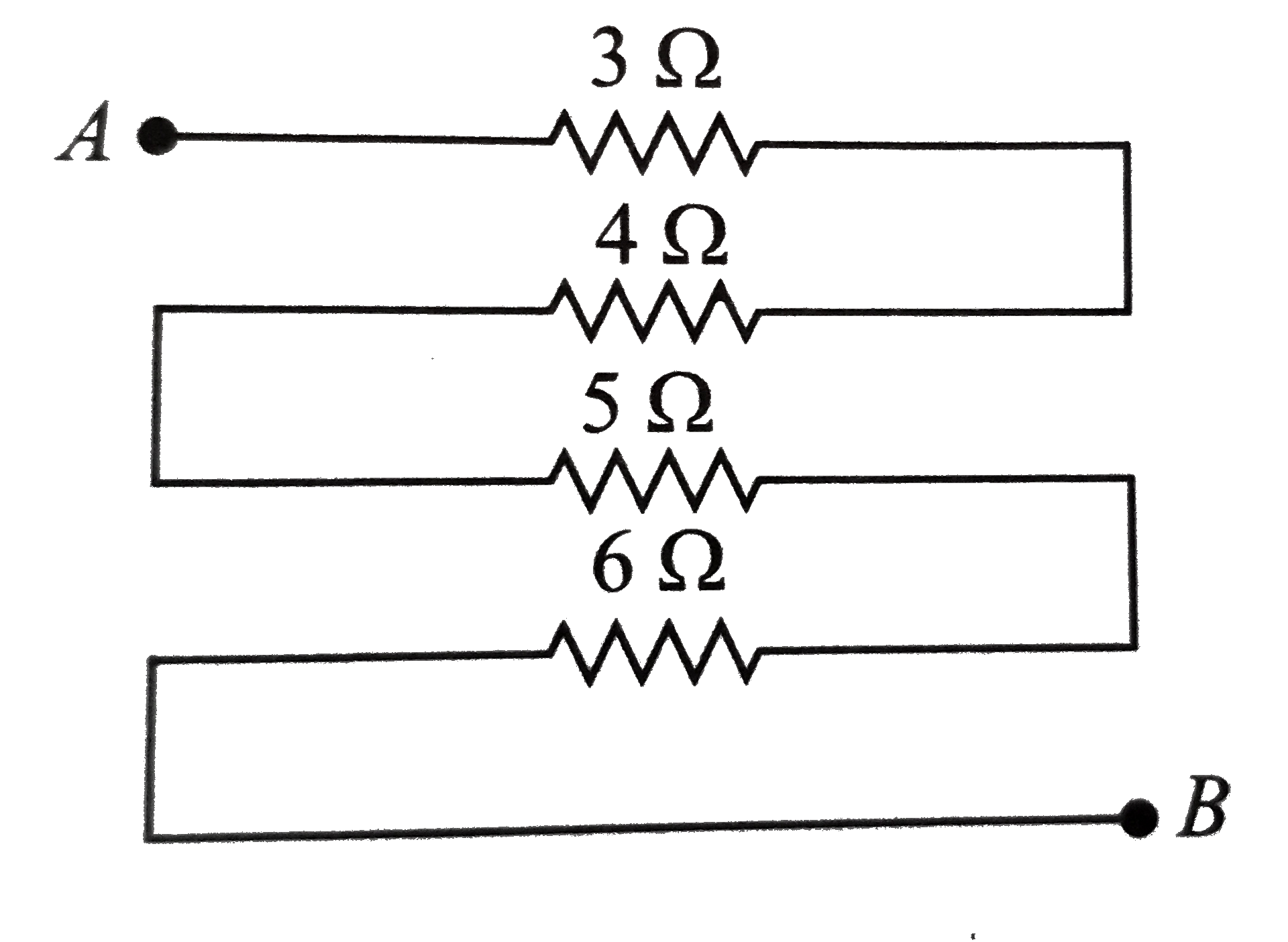 A28B18C26D25
A28B18C26D25
All resistances in fig. 5.34 are in ohm. Find the effective resistance between points A and B.

View Solution"The resistance of a wire is 1 ohm". Explain the statement.
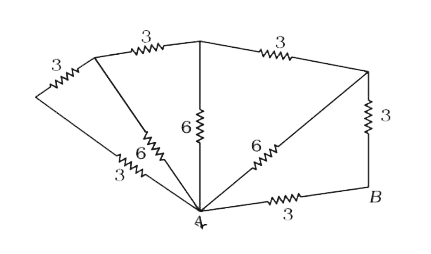
View SolutionAll resistance in the diagram are in ohm
Find the effective resistance (in ohm) between the points A and B
View SolutionFind current through 4ohm resistance
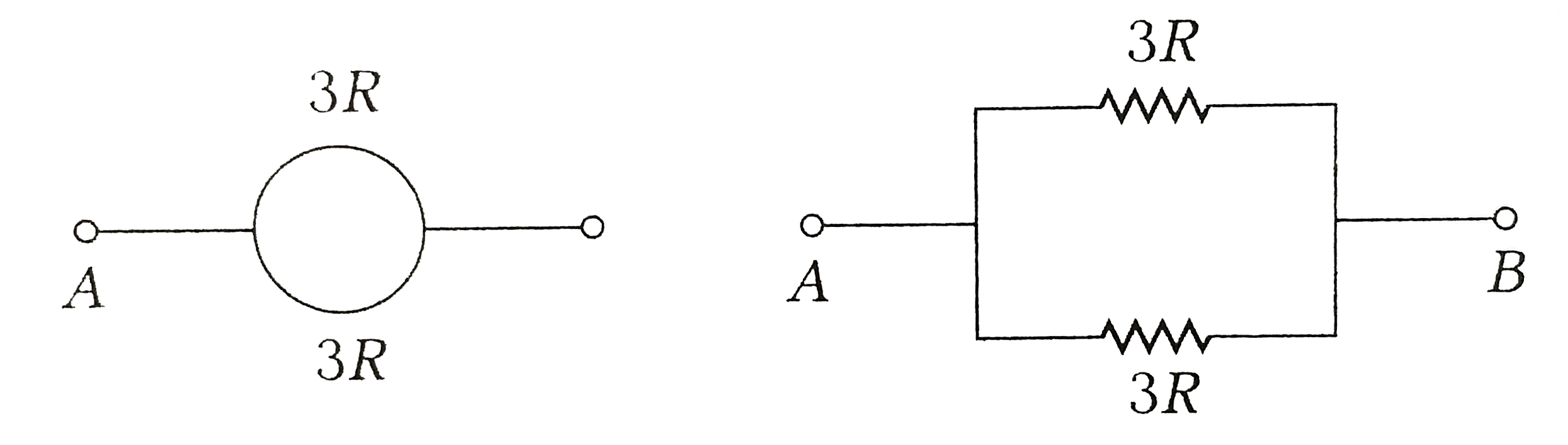
View SolutionA wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
View SolutionThe resistance of the wire is 121 ohm. It is divided into .n. equal parts and they are connected in parallel, then effective resistance is 1 ohm. The value of .n. is
View SolutionA wire has a resistance of 12 ohm . It is bent in the form of equilateral triangle. The effective resistance between any two corners of the triangle is
View Solution
