A circular ring of diameter 20cm has a resistance 0.01Ω How much charge will flow through the ring if it is rotated from positon perpendicular to the uniform magnetic field of B=2T to a position parallel to field?
4 C
6.28 C
3.14 C
2.5 C
The correct Answer is:B
To solve the problem, we need to calculate the charge that flows through a circular ring when it is rotated from a position perpendicular to a magnetic field to a position parallel to the field. Here’s a step-by-step solution:
Step 1: Determine the area of the circular ring
The area A of a circular ring can be calculated using the formula:
A=πr2
where r is the radius of the ring. Given that the diameter is 20 cm, the radius r is:
r=20cm2=10cm=0.1m
Now, substituting the radius into the area formula:
A=π(0.1)2=π(0.01)=0.01πm2
Step 2: Calculate the initial magnetic flux
The initial magnetic flux Φi when the ring is perpendicular to the magnetic field is given by:
Φi=B⋅A⋅cos(0∘)=B⋅A
Substituting the values:
B=2T,A=0.01πm2
Thus,
Φi=2⋅(0.01π)=0.02πWb
Step 3: Calculate the final magnetic flux
When the ring is parallel to the magnetic field, the angle between the magnetic field and the area vector is 90 degrees:
Φf=B⋅A⋅cos(90∘)=0
Step 4: Calculate the change in magnetic flux
The change in magnetic flux ΔΦ is:
ΔΦ=Φf−Φi=0−0.02π=−0.02πWb
Step 5: Calculate the induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−ΔΦΔt
Assuming the time taken for the rotation is t, we have:
E=0.02πtV
Step 6: Calculate the induced current
Using Ohm's law, the induced current I can be calculated as:
I=ER
where R=0.01Ω:
I=0.02π/t0.01=2πtA
Step 7: Calculate the charge that flows
The total charge Q that flows through the ring can be calculated using the relationship:
Q=I⋅t
Substituting the expression for current:
Q=(2πt)⋅t=2πC
Final Answer
Thus, the total charge that flows through the ring is:
Q=2πC≈6.28C
The area A of a circular ring can be calculated using the formula:
A=πr2
where r is the radius of the ring. Given that the diameter is 20 cm, the radius r is:
r=20cm2=10cm=0.1m
Now, substituting the radius into the area formula:
A=π(0.1)2=π(0.01)=0.01πm2
The initial magnetic flux Φi when the ring is perpendicular to the magnetic field is given by:
Φi=B⋅A⋅cos(0∘)=B⋅A
Substituting the values:
B=2T,A=0.01πm2
Thus,
Φi=2⋅(0.01π)=0.02πWb
When the ring is parallel to the magnetic field, the angle between the magnetic field and the area vector is 90 degrees:
Φf=B⋅A⋅cos(90∘)=0
The change in magnetic flux ΔΦ is:
ΔΦ=Φf−Φi=0−0.02π=−0.02πWb
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−ΔΦΔt
Assuming the time taken for the rotation is t, we have:
E=0.02πtV
Using Ohm's law, the induced current I can be calculated as:
I=ER
where R=0.01Ω:
I=0.02π/t0.01=2πtA
The total charge Q that flows through the ring can be calculated using the relationship:
Q=I⋅t
Substituting the expression for current:
Q=(2πt)⋅t=2πC
Thus, the total charge that flows through the ring is:
Q=2πC≈6.28C
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Taking it together
Explore 119 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrance special format questions
Explore 17 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Example
Explore 71 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
A circular conducting ring is rotated about one of its diameter in a magnetic field
View SolutionA closed coil consists of 500 turns has area 4cm2 and a resistance of 50Ω. The coil is kept with its plane perpendicular to a uniform magnetic field of 0.2Wbm2. Calculate the amount charge flowing through the coil if it is rotated through 180∘
View SolutionA closed coil having 100 turns is rotated in a uniform magnetic field B=4.0X10−4 T about a diameter which is perpendicular to the field. The angular velocity of rotation is 300 revolutions per minute. The area of the coil is 25cm2 and its resistance is 4.0Ω. Find (a) the average emf developed in the half a turn form a position where the coil is perpendicular to the magnetic field, (b) the average emf in a full turn and (c) the net charge displaced in part (a).
View SolutionA circular coil of 60 turns and radius 4 cm carries current of 1 A . How much work will be done in rotating the coil through 90∘ . It is suspended freely in uniform magnetic field 0.2T.
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field.If T=10sec, find the instant of time at which EMF will be maximum & minimum respectively :
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively. (Figure:
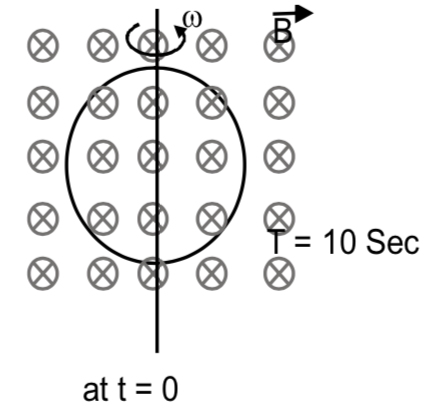 )
)
View SolutionA wire loop that encloses an area of 20cm2 has a resistance of 10Ω The loop is placed in a magnetic field of 2.4 T with its plane perpendicular to the field . The loop is suddenly removed from the field. How much charge flows past a given point in the wire ?
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA circular coil of 500 turns of wire has an enclosed area of 0.1 m2 per turn. It is kept perpendicular to a magnetic field of induction 0.2 T and rotated by 180∘ about a diameter perpendicular to the field in 0.1 s. How much charge will pass when the coil is connected to a galvanometer with a combined resistance of 50 Ω.
View SolutionA metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View Solution