A force F is applied at center of a uniform round object of mass m radius R and moment of inertia about its centre of mass Icm. Find (if IcmmR2=k).
(a) Acceleration of center of the round object if it rolls without slipping.
(b) Minimum coefficient of fricition required so that the round object rolls without slipping.
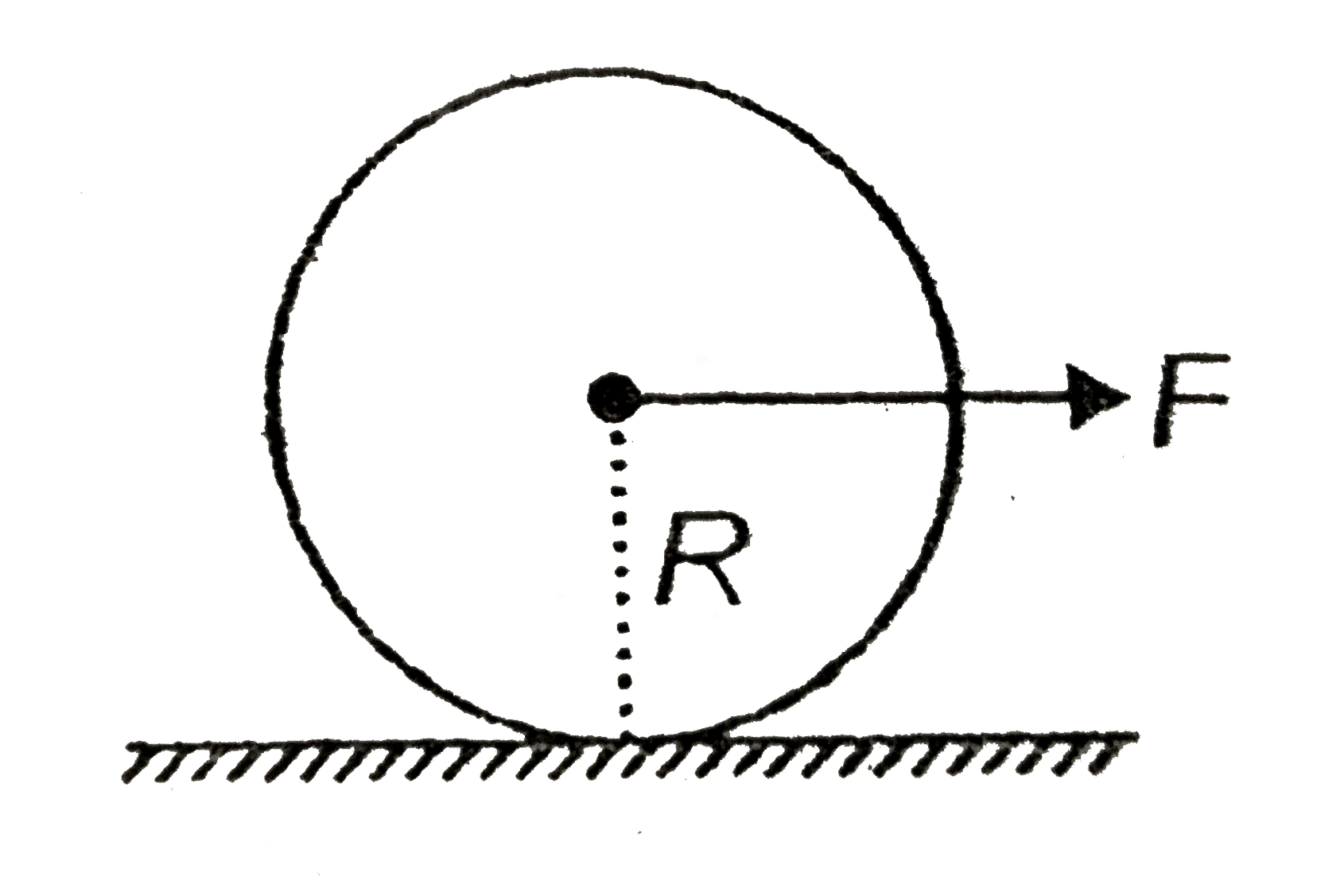
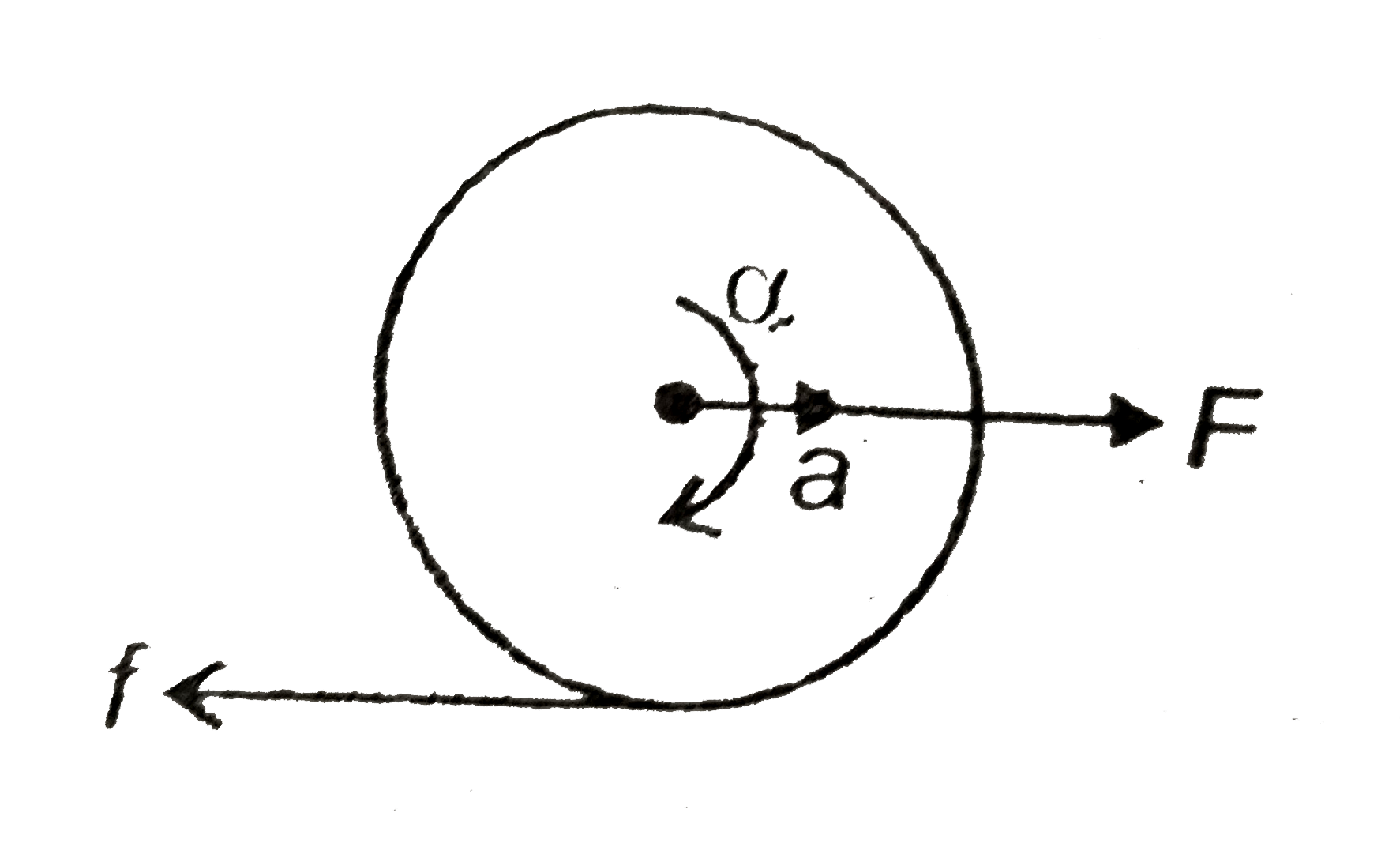
Equation for translatory motion
F−f=ma……..(1)
Equation for rotatory motion
fR=Icmα……..(2)
Condition for no slipping
a=Rα……..(3)
By solving the equations
F−IcmaR2=ma
a=Fm+IcmR2
=Fm[1+IcmmR2]
=Fm(1+k)
f=IcmFmR2(1+k)=kF(1+k)
Thus μminmg=kF1+k
⇒μmin=(k1+k)Fmg
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration4videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE21videos
TEST 1
Similar Questions
A force (F=Mg) is applied on the top of a circular ring of mass M and radius R kept on a rough horizontal surface. If the ring rolls without slipping, then minimum coefficient of friction required is
_PHY_E05_236_Q01.png) View Solution
View SolutionA force F is applied on a disc at it's centre. Find acceleration of center of mass in the case of pure rolling and also find minimum coefficient of fricition required for pure rolling.
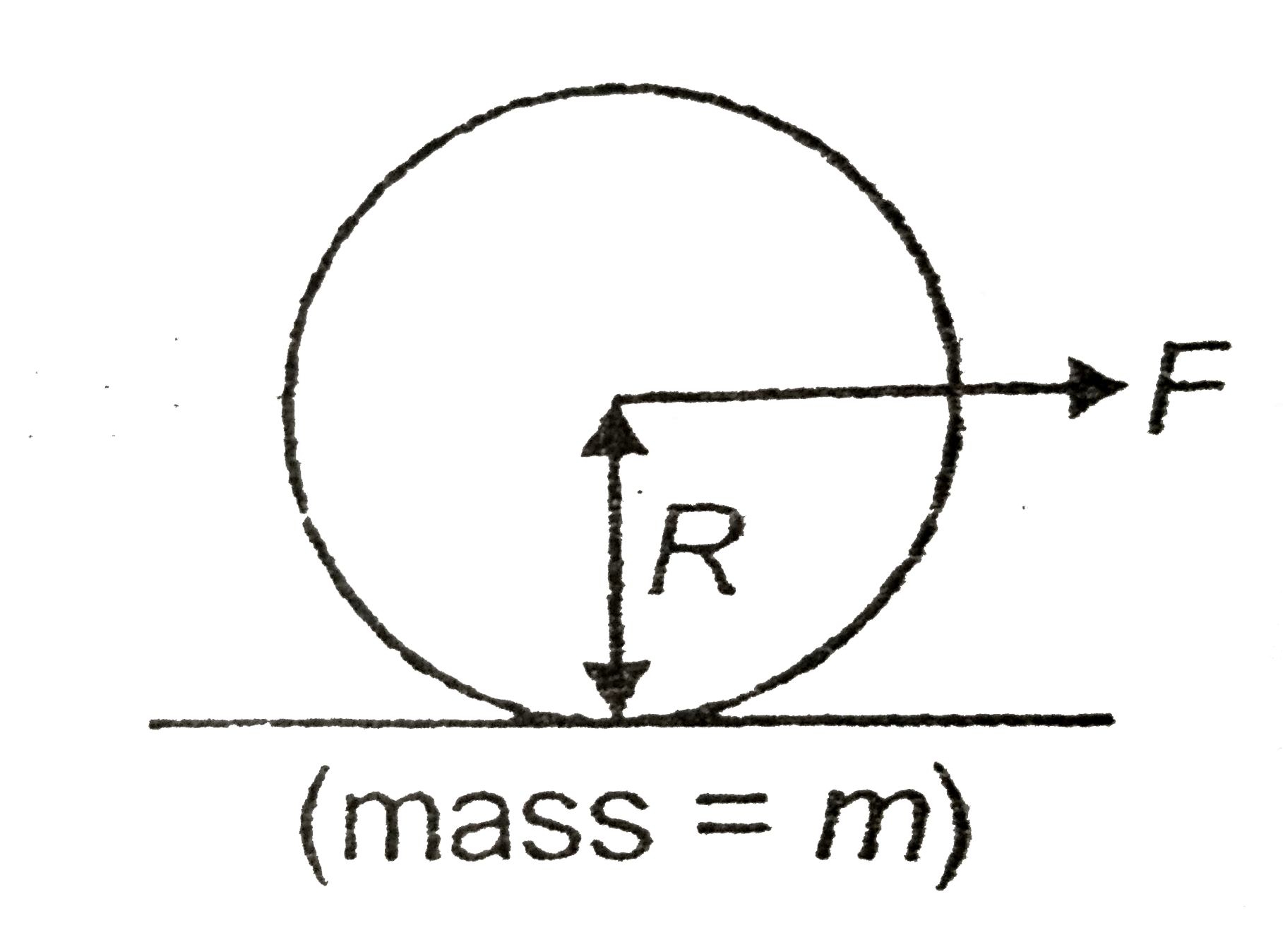 View Solution
View Solution
Knowledge Check
- Question 1 - Select One

A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.Aa. Acceleration of disc = 2F/3mBb. Friction force between disc and surface = 2F/3Cc. Acceleration of disc = 6F/5mDd. Friction force between disc and surface is F/3
A sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
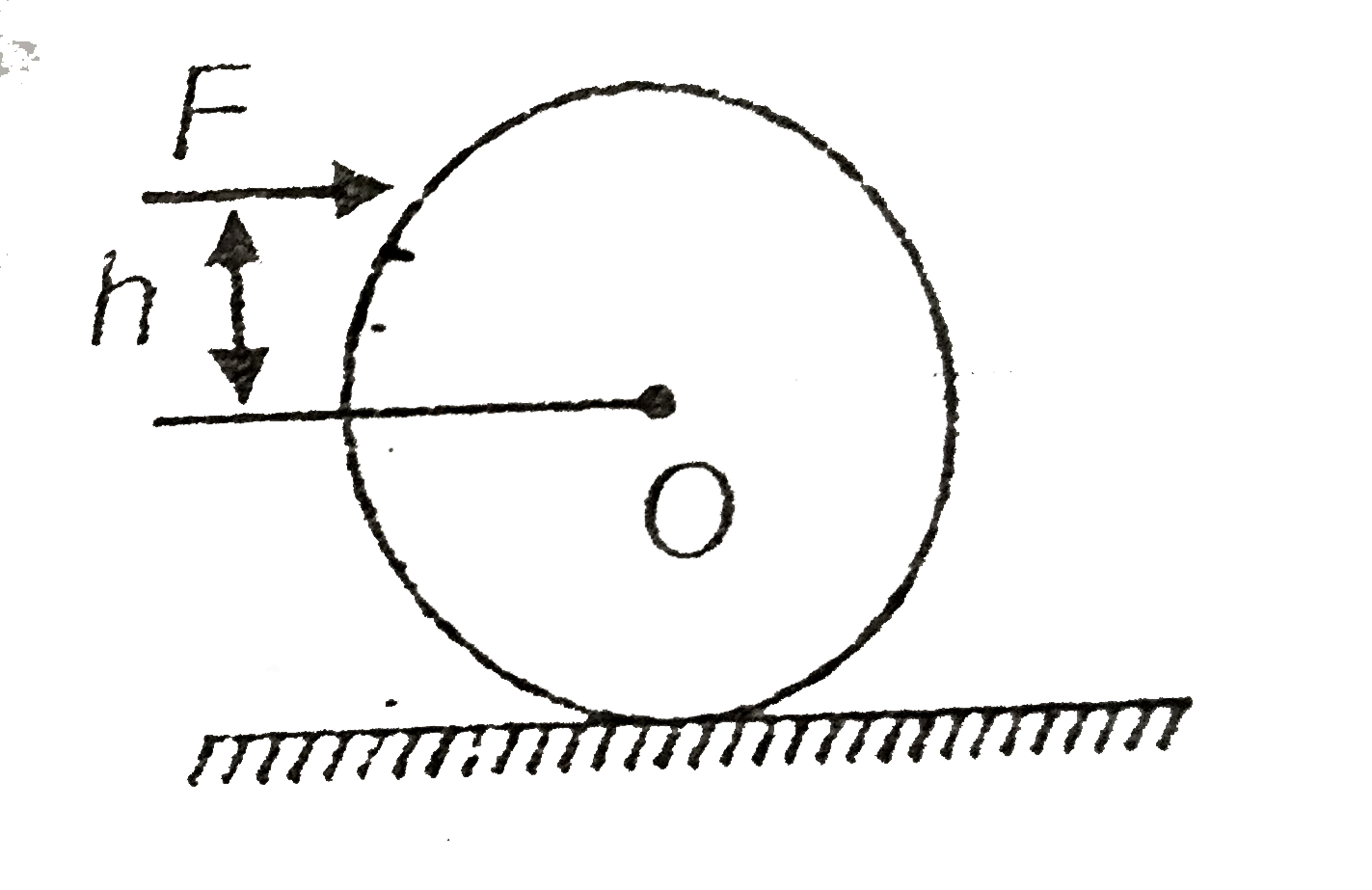 View Solution
View SolutionA uniform round object of mass m, radius R and moment of inertia about its centre of mas Icm is thrown with speed v. (Without any rotation) on a rough horizontal surface of coefficient of fricition μ. Find (take IcmmR2=k)
(a) Time after which slipping stops
(b) Speed of the round object after slipping stops
(c) Angular speed of the round object after slipping stopsView Solution
A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.View Solution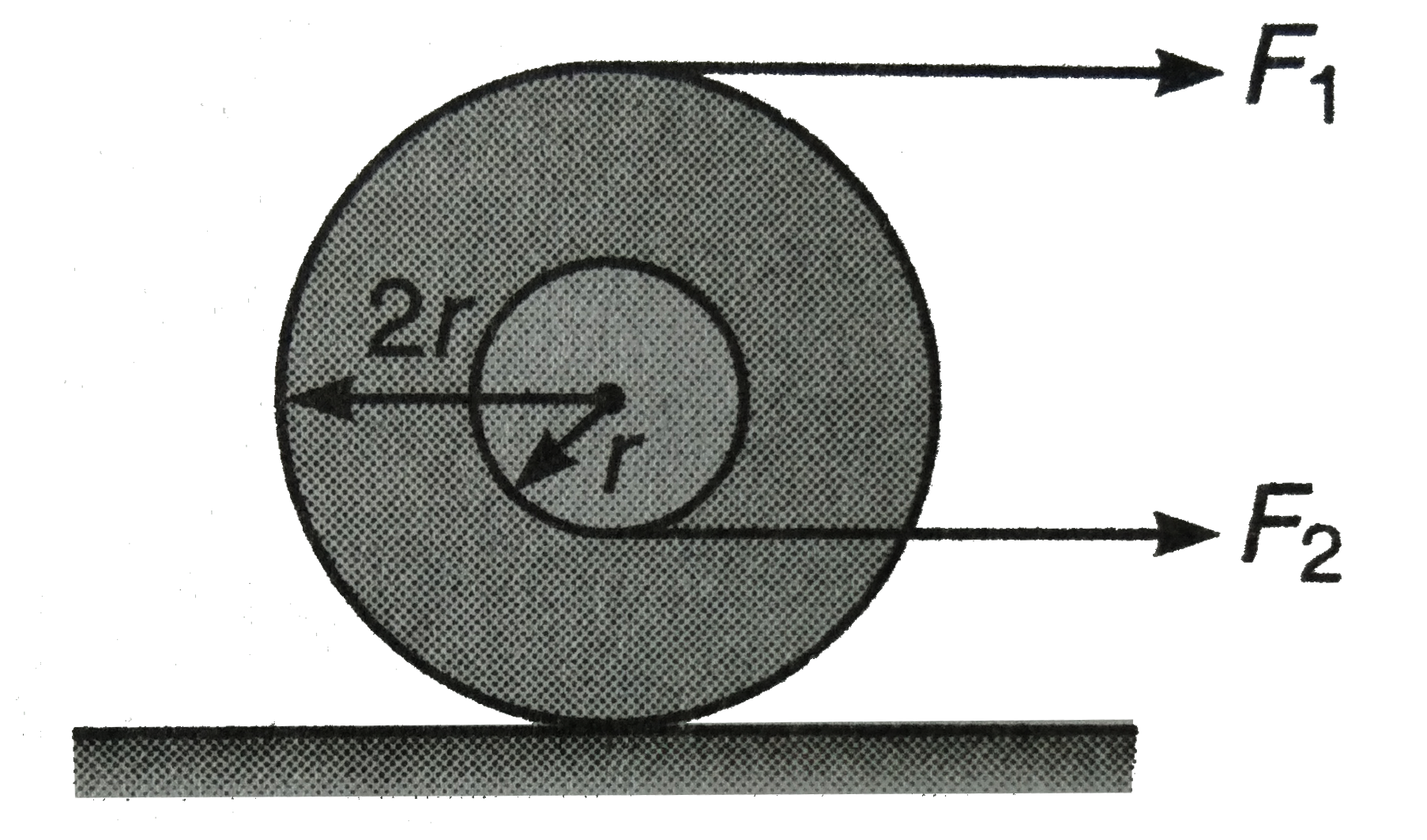
Two forces F1 and F2 are applied on a spool of mass M and moment of inertia I about an axis passing through its centre of mass. Find the ratio F1F2. So that the force of friction is zero. Given that I<2Mr2.View SolutionA uniform round object of mass M, radius R and moment of inertia about its centre of mass Icm has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the celling and the object is released from rest. Find the acceleration of centre of the object and tension n the string. [ Take IcmMR2=k]
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
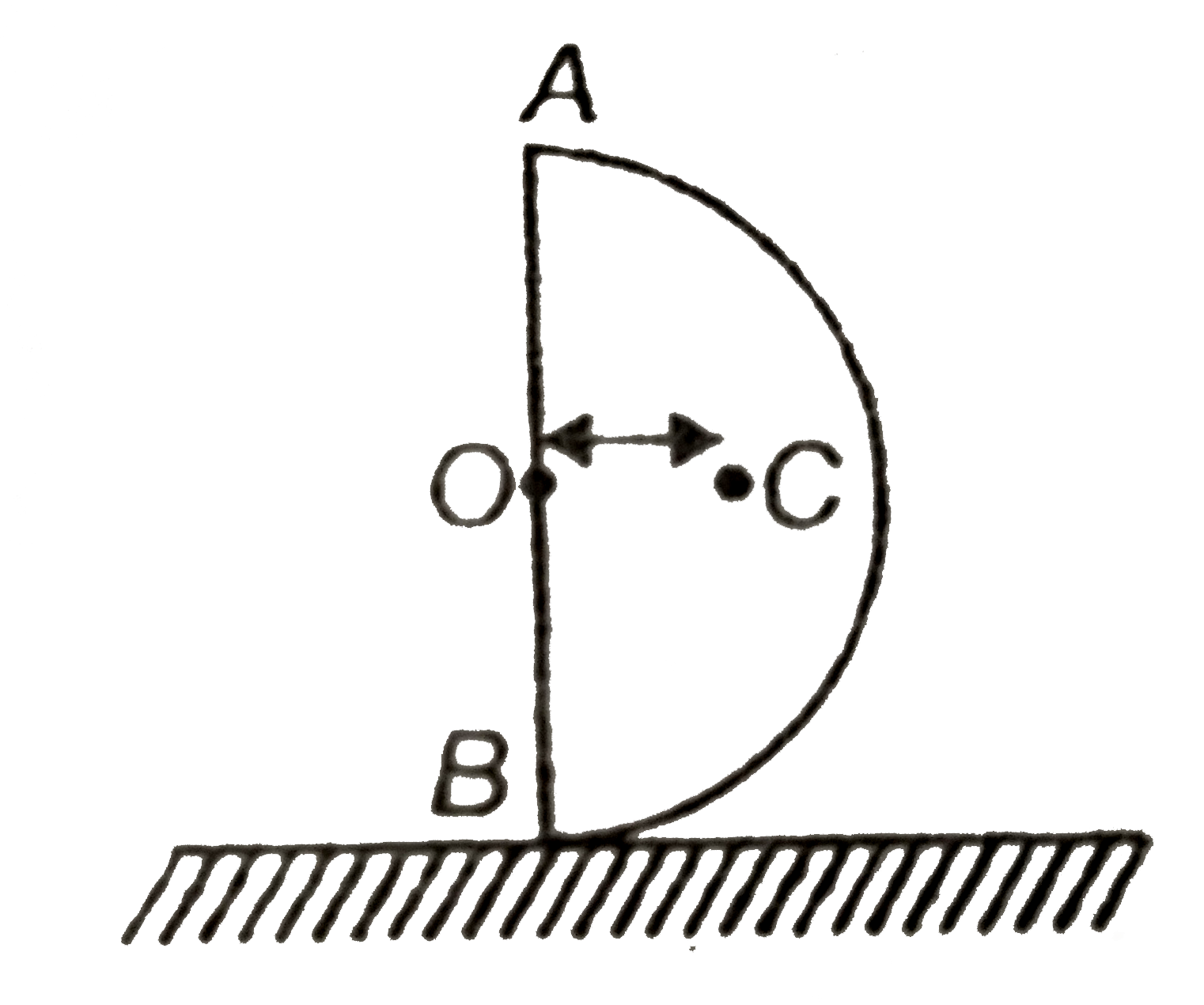
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.View Solution

