A force F is applied on a disc at it's centre. Find acceleration of center of mass in the case of pure rolling and also find minimum coefficient of fricition required for pure rolling.
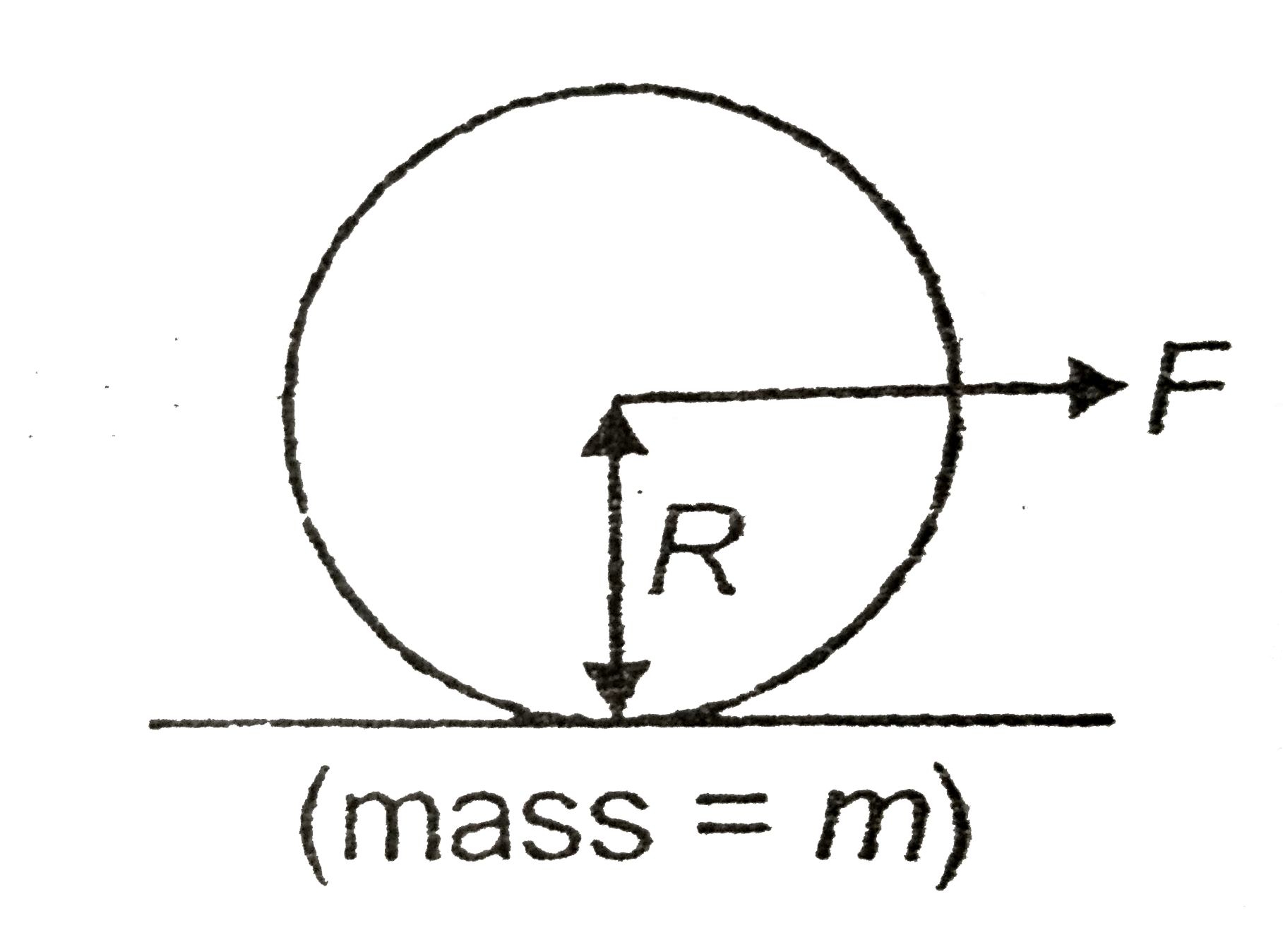

Let the friction force acting on disc be fr, acceleration of centre of mass is a and angular acceleration is α.
We have three unknowns
(i) a
(ii)α
(iii)fr
We require 3 equations to solve them
Translatory Motion
F−fr=ma......(i)
Rotatory Motion
r⋅fr=mr22⋅α........(ii)
Condition of no slipping
a=rα..........(iii)
By solving (ii) & (iii)
fr=ma2, F=3ma2⇒a=2F3m, fr=m2×2F3m, fr=F3
Now, fr≤μN
⇒F3≤μmg
⇒μ≥F3mg
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration4videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE21videos
TEST 1
Similar Questions
Derive an expression for the acceleration of a solid cylinder rolling without slipping down an inclined plane. Also find the minimum coefficient of friction required for pure rolling
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination '0' then the minimum coefficient of friction required to support pure rolling is
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination 45°, then the minimum coefficient of friction required to support pure rolling is
View SolutionA sphere of mass m rolls without slipping on an inclined plane of inclination θ. Find the linear acceleration of the sphere and the force of friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?
View SolutionA force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
 View Solution
View Solution
Assertion: A horizontal force F is applied at the centre of solid sphere placed over a plank. The minimum coefficient of friction between plank and sphere required for pure rolling is μ1 when plank is kept at rest ad μ2 when plank can move, then μ2<μ1
Reason: Work done by frictional force on the sphere in both cases is zero.View SolutionA force F is applied at the centre of a disc of mass M. The minimum value of coefficient of friction of the surface for rolling is
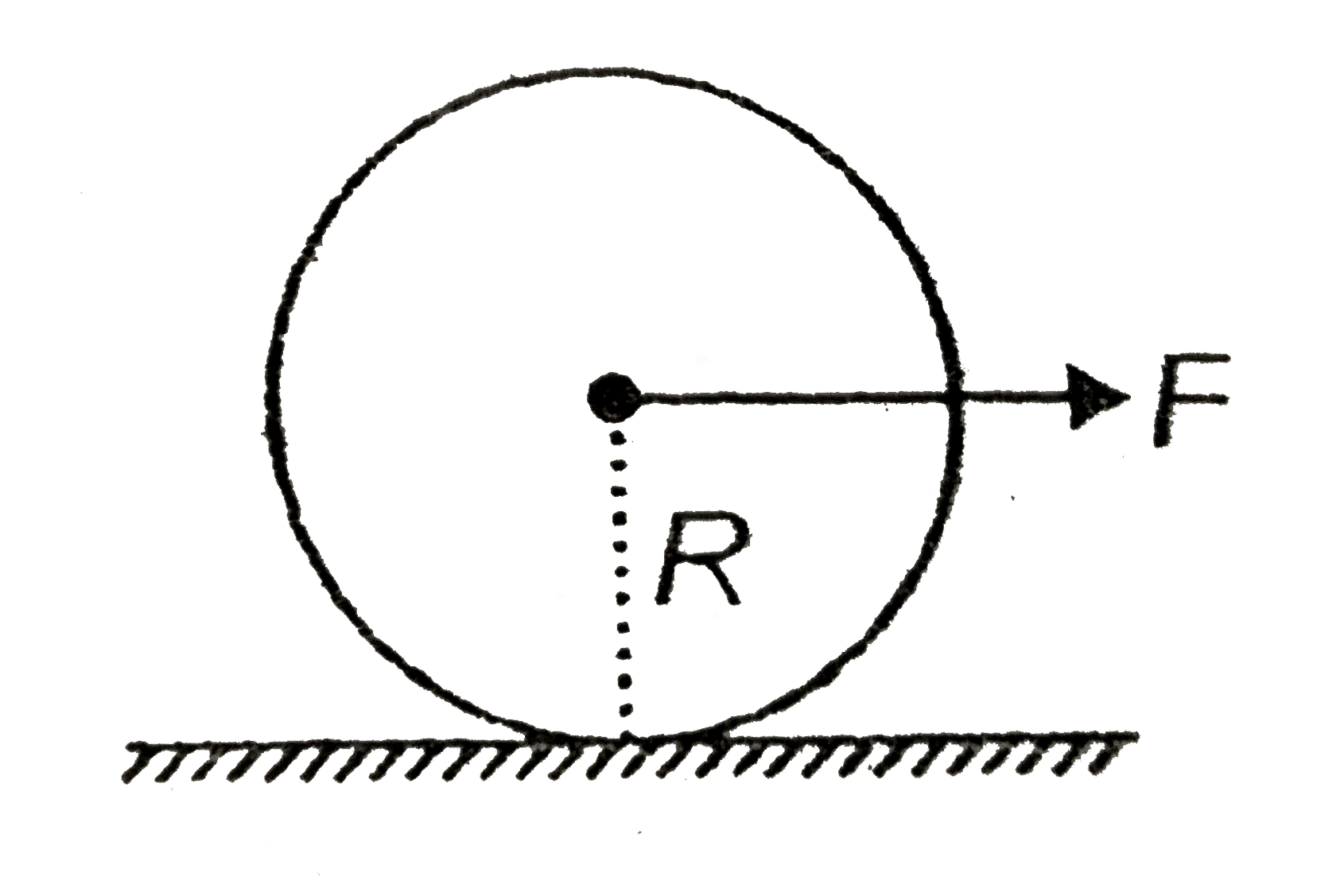
View SolutionA force F is applied at center of a uniform round object of mass m radius R and moment of inertia about its centre of mass Icm. Find (if IcmmR2=k).
(a) Acceleration of center of the round object if it rolls without slipping.
(b) Minimum coefficient of fricition required so that the round object rolls without slipping.
 View Solution
View SolutionA spherical shell of radius R is rolling down an incline of inclination θ without slipping. Find minimum value of coefficient of friction.
 View Solution
View SolutionA horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation is μ,find 100μ?(√3=1.74)
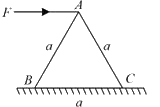 View Solution
View Solution

