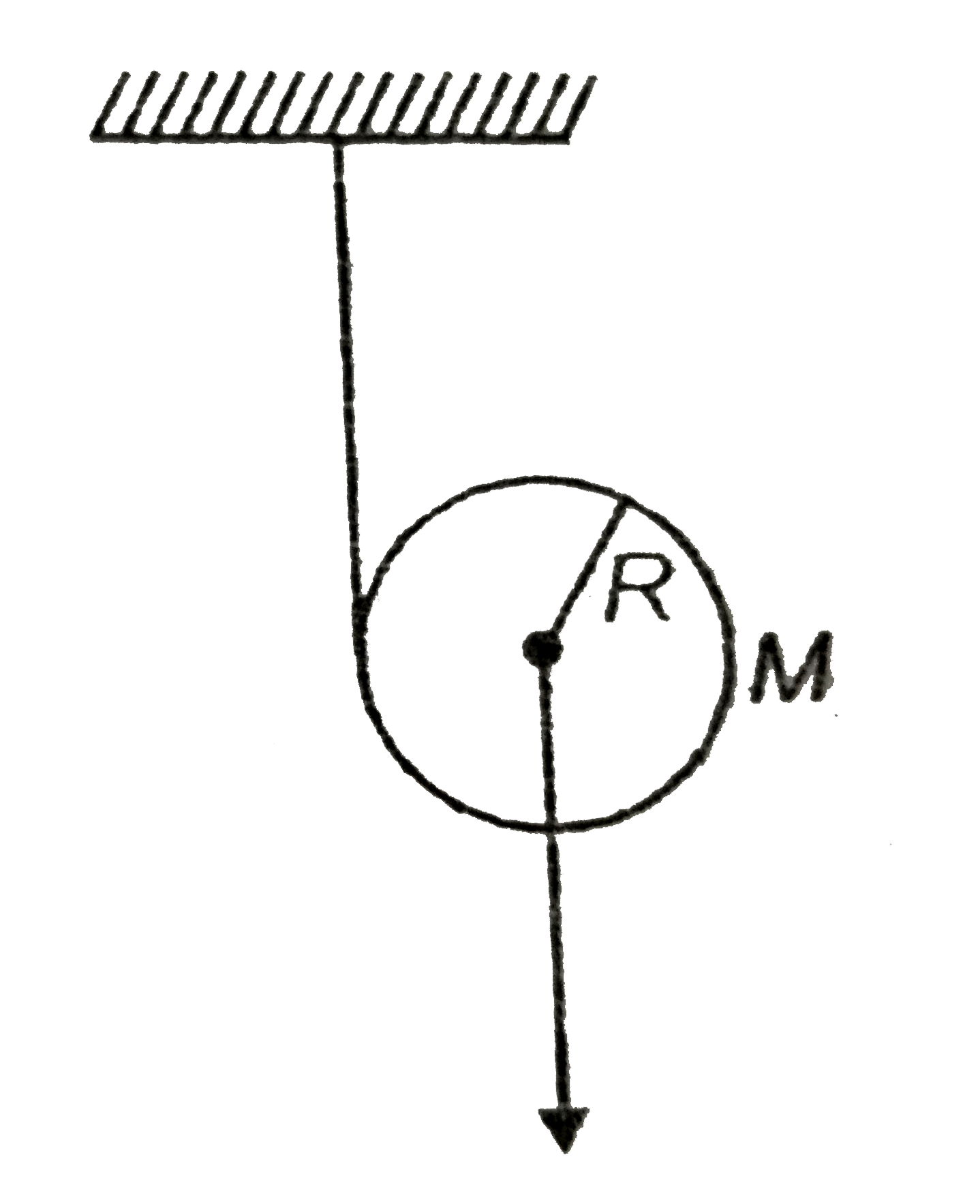
A uniform round object of mass M, radius R and moment of inertia about its centre of mass Icm has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the celling and the object is released from rest. Find the acceleration of centre of the object and tension n the string. [ Take IcmMR2=k]
To solve this problem, we need to analyze the forces acting on the uniform round object and apply Newton's second law. Let's go through the solution step by step.
Step 1: Identify the forces acting on the object
The forces acting on the object are:
- The weight of the object, W=Mg, acting downward.
- The tension in the string, T, acting upward.
Step 2: Apply Newton's second law
According to Newton's second law, the net force acting on the object is equal to the mass of the object multiplied by its acceleration. Thus, we can write:
Mg−T=Ma
where a is the acceleration of the center of mass of the object.
Step 3: Relate linear acceleration to angular acceleration
The object is also rotating due to the tension in the string. The torque τ caused by the tension about the center of mass is given by:
τ=T⋅R
This torque is also related to the angular acceleration α of the object:
τ=Icm⋅α
where Icm is the moment of inertia of the object about its center of mass.
Step 4: Relate linear acceleration to angular acceleration
The linear acceleration a of the center of mass is related to the angular acceleration α by:
a=R⋅α⟹α=aR
Step 5: Substitute the angular acceleration into the torque equation
Substituting α=aR into the torque equation gives:
T⋅R=Icm⋅aR
Rearranging this, we find:
T=Icm⋅aR2
Step 6: Substitute T back into the force equation
Now, we can substitute this expression for T back into the equation from Step 2:
Mg−Icm⋅aR2=Ma
Step 7: Solve for acceleration a
Rearranging the equation gives:
Mg=Ma+Icm⋅aR2
Factoring out a on the right side:
Mg=a(M+IcmR2)
Thus, we can solve for a:
a=MgM+IcmR2
Step 8: Substitute IcmMR2=k
Given that IcmMR2=k, we can rewrite the expression for a:
a=MgM+Mk=g1+k
Step 9: Find the tension T
Now, substituting a back into the expression for T:
T=Icm⋅aR2
Substituting Icm=kMR2 and a=g1+k:
T=kMR2⋅g1+kR2=kMg1+k
Final Answers
- The acceleration of the center of the object is:
a=g1+k
- The tension in the string is:
T=kMg1+k
The forces acting on the object are:
- The weight of the object, W=Mg, acting downward.
- The tension in the string, T, acting upward.
According to Newton's second law, the net force acting on the object is equal to the mass of the object multiplied by its acceleration. Thus, we can write:
Mg−T=Ma
where a is the acceleration of the center of mass of the object.
The object is also rotating due to the tension in the string. The torque τ caused by the tension about the center of mass is given by:
τ=T⋅R
This torque is also related to the angular acceleration α of the object:
τ=Icm⋅α
where Icm is the moment of inertia of the object about its center of mass.
The linear acceleration a of the center of mass is related to the angular acceleration α by:
a=R⋅α⟹α=aR
Substituting α=aR into the torque equation gives:
T⋅R=Icm⋅aR
Rearranging this, we find:
T=Icm⋅aR2
Now, we can substitute this expression for T back into the equation from Step 2:
Mg−Icm⋅aR2=Ma
Rearranging the equation gives:
Mg=Ma+Icm⋅aR2
Factoring out a on the right side:
Mg=a(M+IcmR2)
Thus, we can solve for a:
a=MgM+IcmR2
Given that IcmMR2=k, we can rewrite the expression for a:
a=MgM+Mk=g1+k
Now, substituting a back into the expression for T:
T=Icm⋅aR2
Substituting Icm=kMR2 and a=g1+k:
T=kMR2⋅g1+kR2=kMg1+k
- The acceleration of the center of the object is:
a=g1+k
- The tension in the string is:
T=kMg1+k
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
A disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
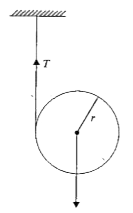
View SolutionOn the surface of a solid cylinder of mass 2 kg and radius 25 cm a string is wound several times and the end of the string is held stationary while the cylinder is released from rest. What is the acceleration of the cylinder and the tension in the string ?
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-

View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
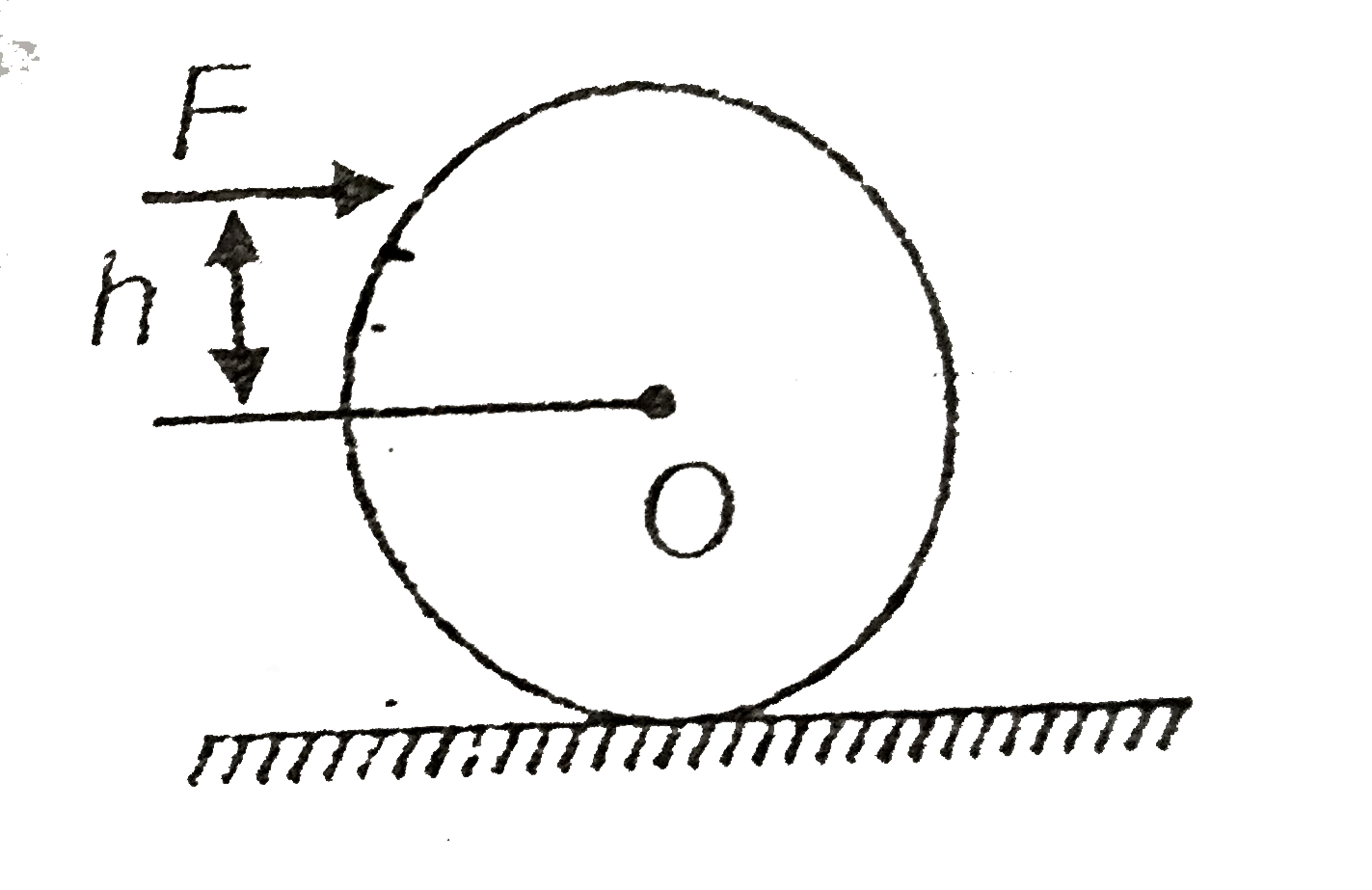
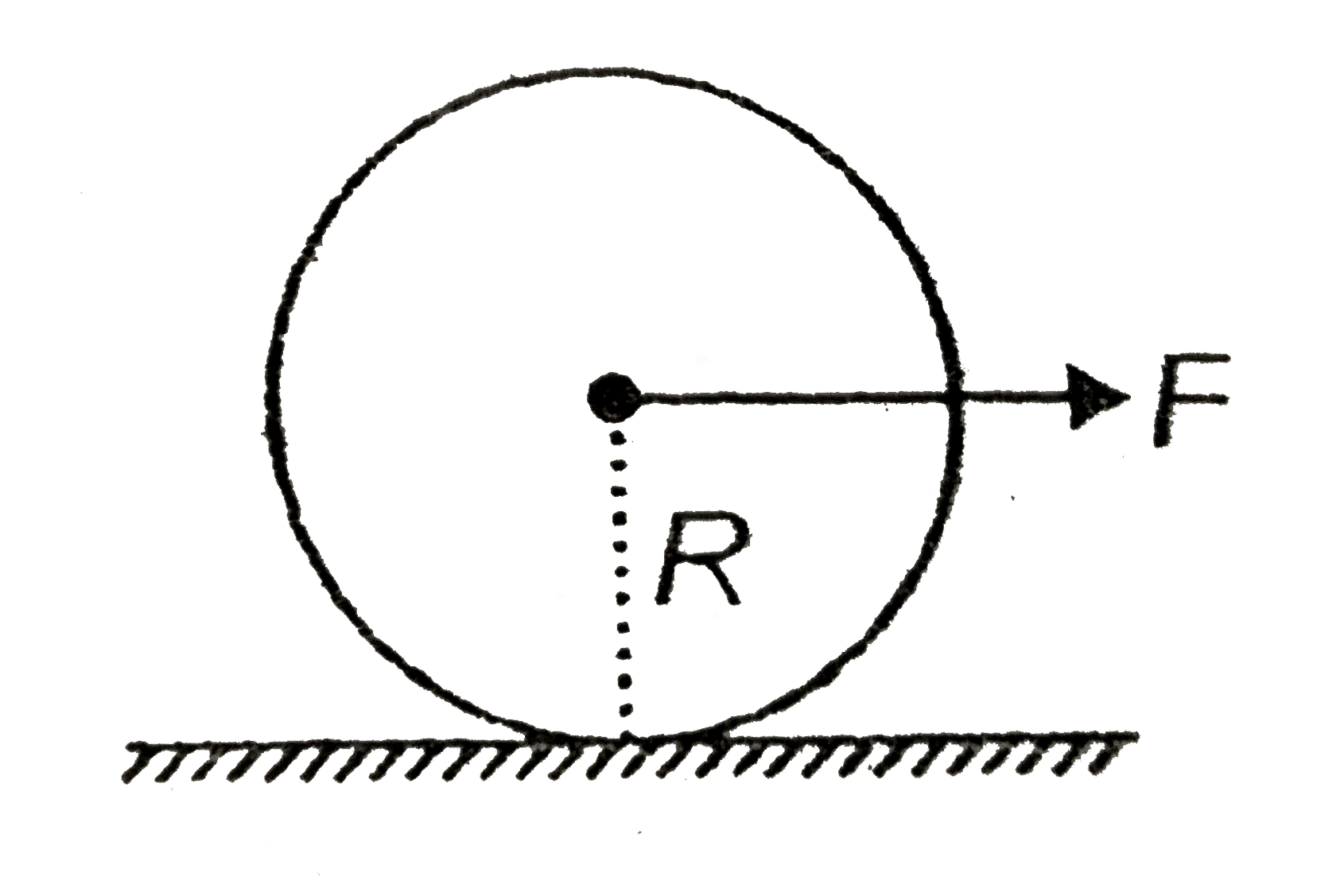
View SolutionA force F is applied at center of a uniform round object of mass m radius R and moment of inertia about its centre of mass Icm. Find (if IcmmR2=k).
(a) Acceleration of center of the round object if it rolls without slipping.
(b) Minimum coefficient of fricition required so that the round object rolls without slipping.
View Solution
A body of mass m, radius R and moment of inertia I (about an axis passing through the centre of mass and perpendicular to plane of motion) is released from rest over a sufficiently rough ground (to provide accelerated pure rolling) find linear acceleration of the body.
View SolutionA uniform round object of mass m, radius R and moment of inertia about its centre of mas Icm is thrown with speed v. (Without any rotation) on a rough horizontal surface of coefficient of fricition μ. Find (take IcmmR2=k)
(a) Time after which slipping stops
(b) Speed of the round object after slipping stops
(c) Angular speed of the round object after slipping stops
View Solution
