A uniform round object of mass m, radius R and moment of inertia about its centre of mas Icm is thrown with speed v. (Without any rotation) on a rough horizontal surface of coefficient of fricition μ. Find (take IcmmR2=k)
(a) Time after which slipping stops
(b) Speed of the round object after slipping stops
(c) Angular speed of the round object after slipping stops
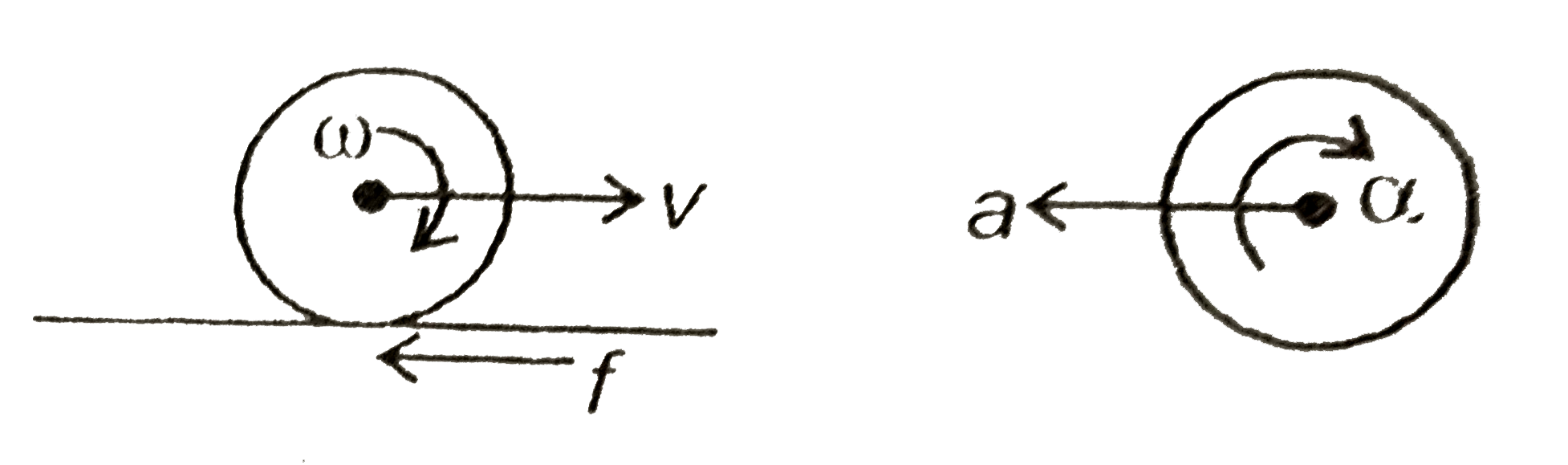
Force eqution of translatory motion
f=ma
f=μN=μmg
a=μg
Equation of motion
v=v0−at
v=v0−μgt
Torque equation of rotatory motion
fR=Icmα
α=μmgRIcm
ω=αt
ω=μmgRtIcm
For pure rolling
v=Rω
⇒v0−μgt=RμmgRtIcm
⇒v0=tμg[1+1k] [∵IcmmR2=k]
⇒t=v0kμg(1+k)⇒v=v0−μg(v0k)(1+k)μg
⇒v=v01+k−k1+k]⇒v=v01+k
⇒ω=v0R(1+k)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
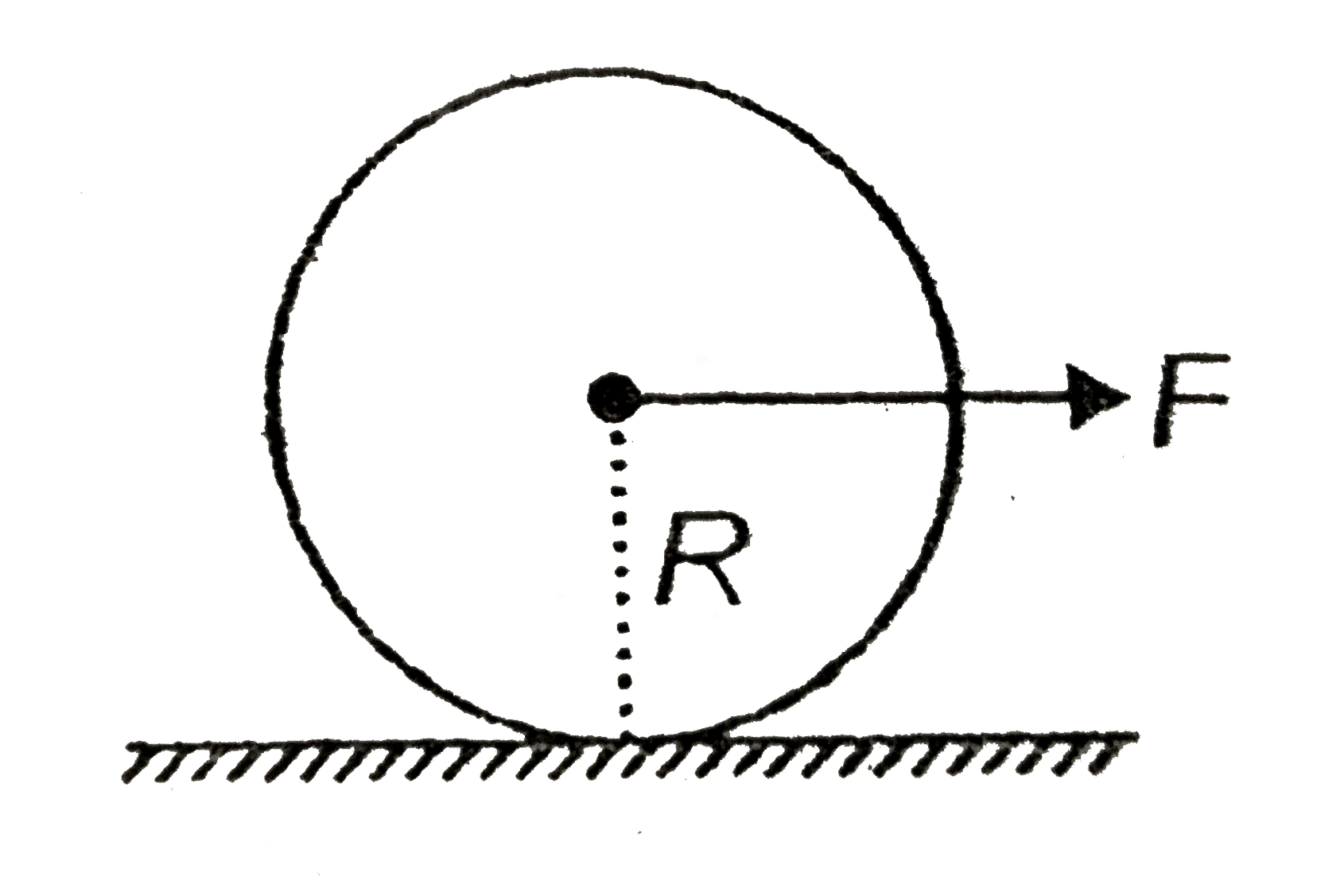
A force F is applied at center of a uniform round object of mass m radius R and moment of inertia about its centre of mass Icm. Find (if IcmmR2=k).
(a) Acceleration of center of the round object if it rolls without slipping.
(b) Minimum coefficient of fricition required so that the round object rolls without slipping.
View SolutionA uniform round object of mass M, radius R and moment of inertia about its centre of mass Icm has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the celling and the object is released from rest. Find the acceleration of centre of the object and tension n the string. [ Take IcmMR2=k]
View Solution
Knowledge Check
A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
AωoμkR2gBωog2μkRC2ωoRμkgDωoR2μkg
A ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA round uniform body of radius R, mass M and moment of inertia 'I' rolls down (without slipping) and inclined plane making an angle θ with the horizontal. Then its acceleration is.
View SolutionA ring of mass m and radius R is placed on a rough horizontal surface (co-efficient of friction μ) with velocity of C.M.v0 and angular speed 2V0R as shown in figure. Initially the ring is rolling with slipping but attains pure rolling motion after some time t. Then
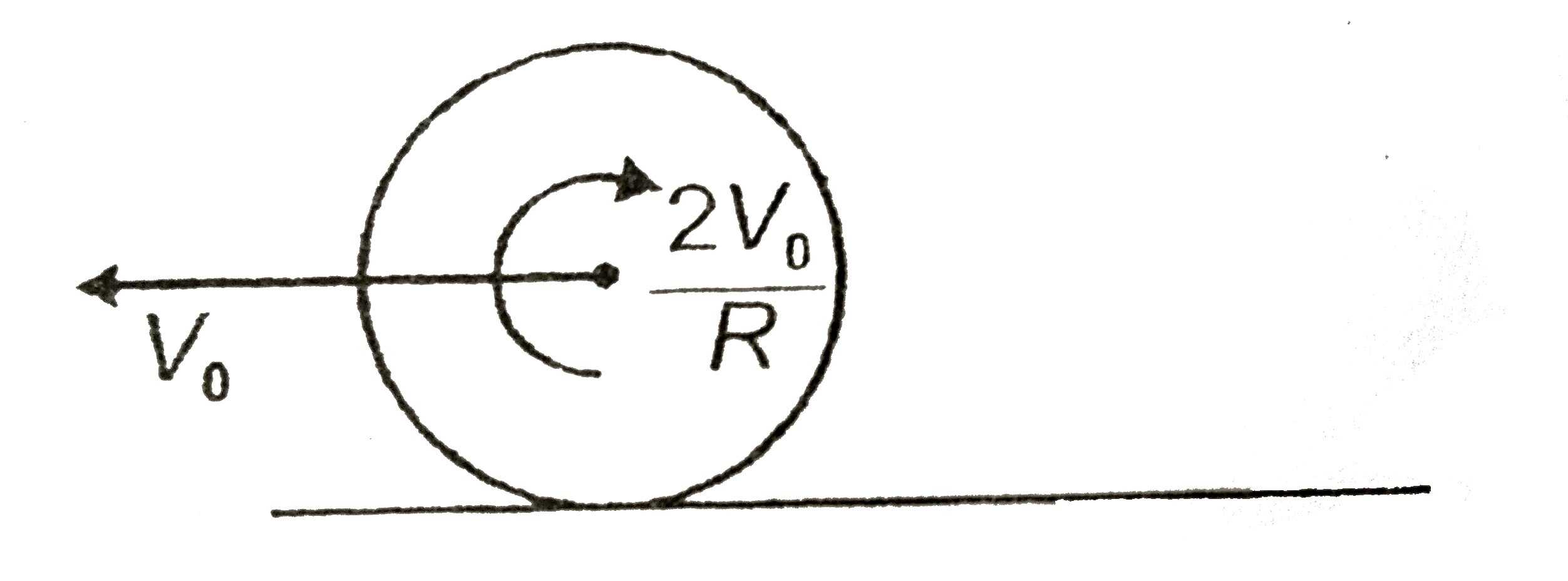
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
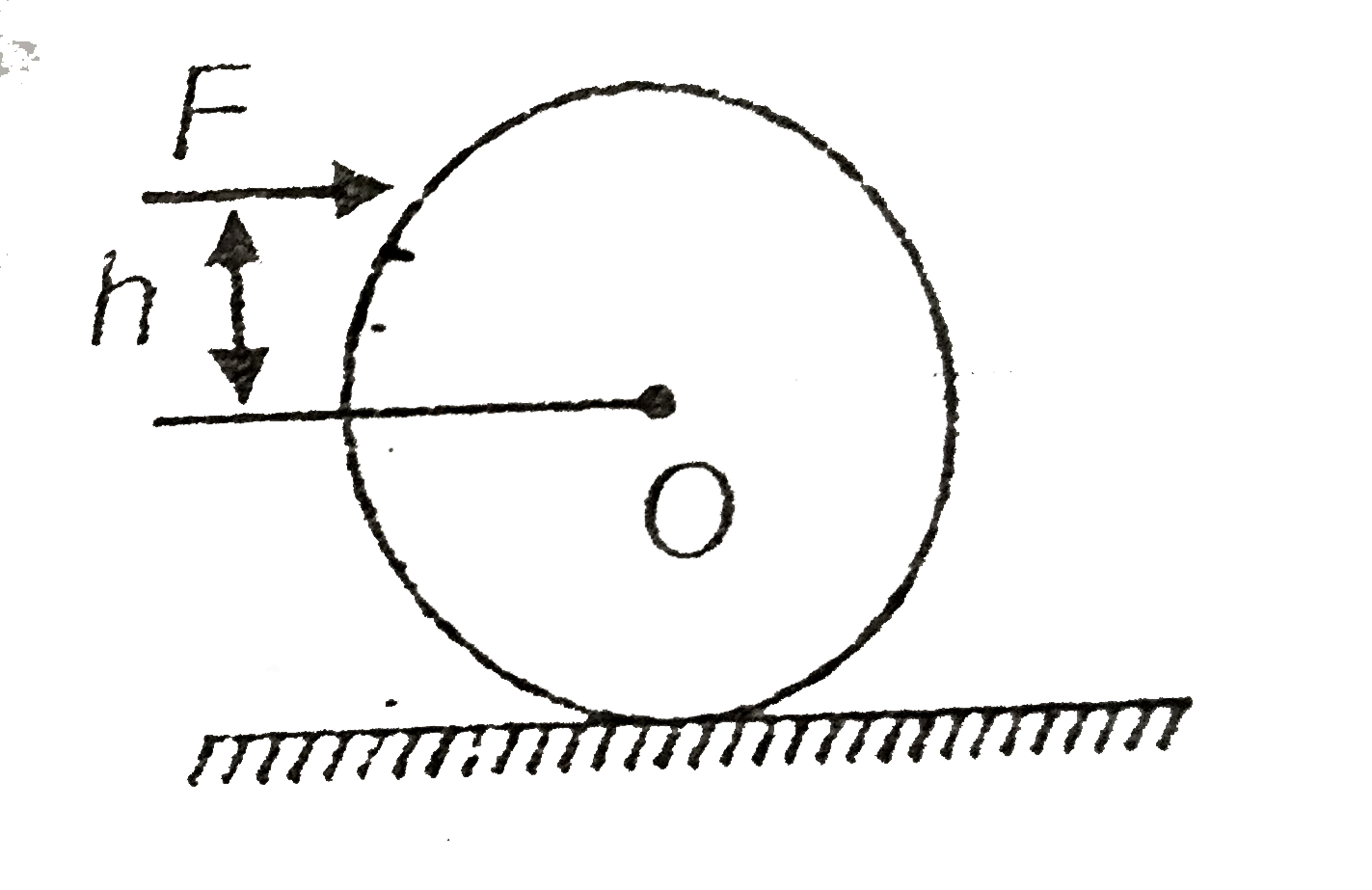
View Solution
solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slipping
View SolutionA uniform disc of mass m and radius R is rotated about an axis passing through its center and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View SolutionA uniform rod of mass m and length l is released from rest from its vertical position by giving a gently push. In consequence, the end of the rod collides at P after rotating about the smooth horizontal axis O. If the coefficient of restitution e=(12). Find the: a. angular speed of the rod just after the impact.
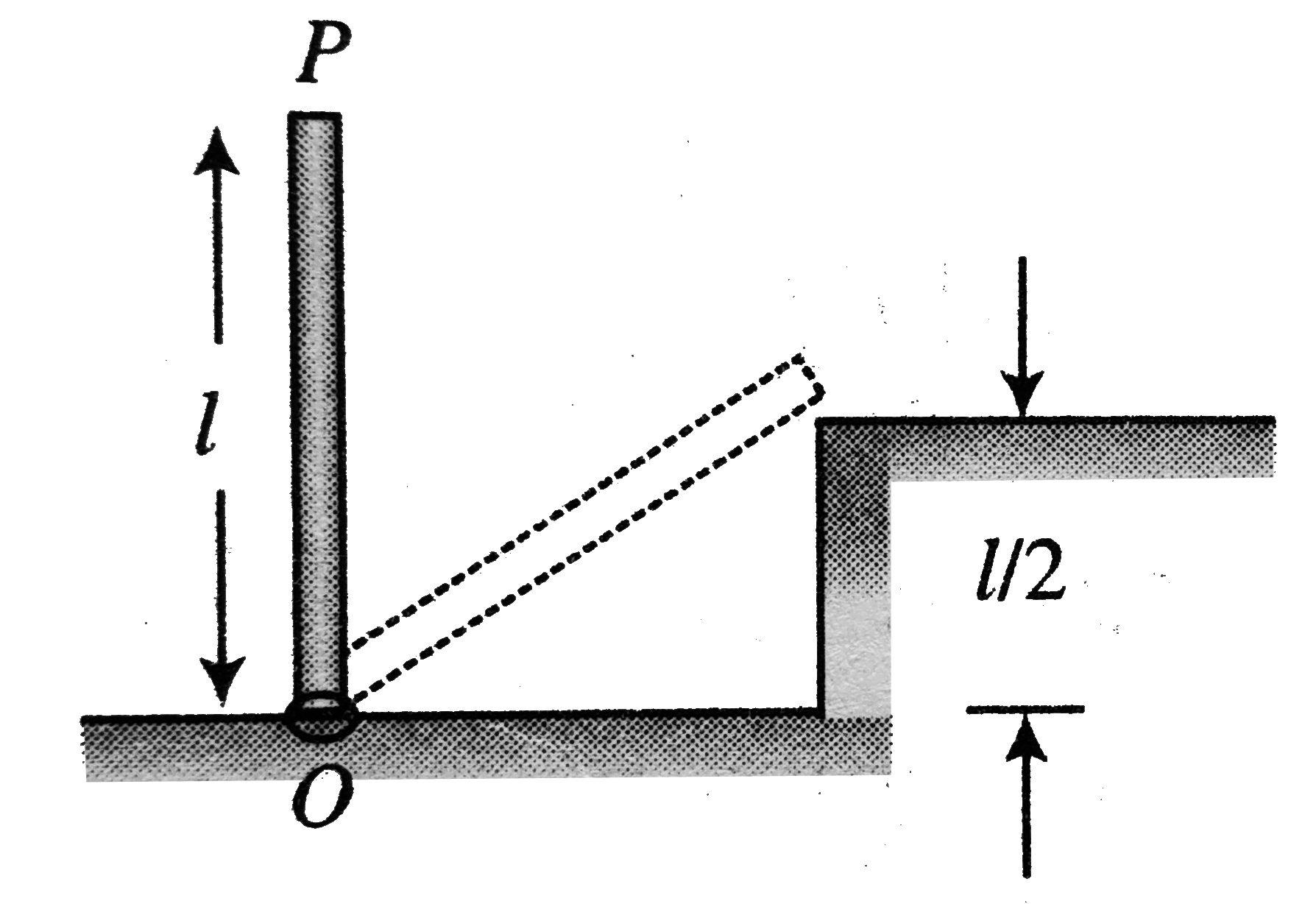
b. energy loss during collision. c. maximum angle rotated by rod after collision.
View Solution
