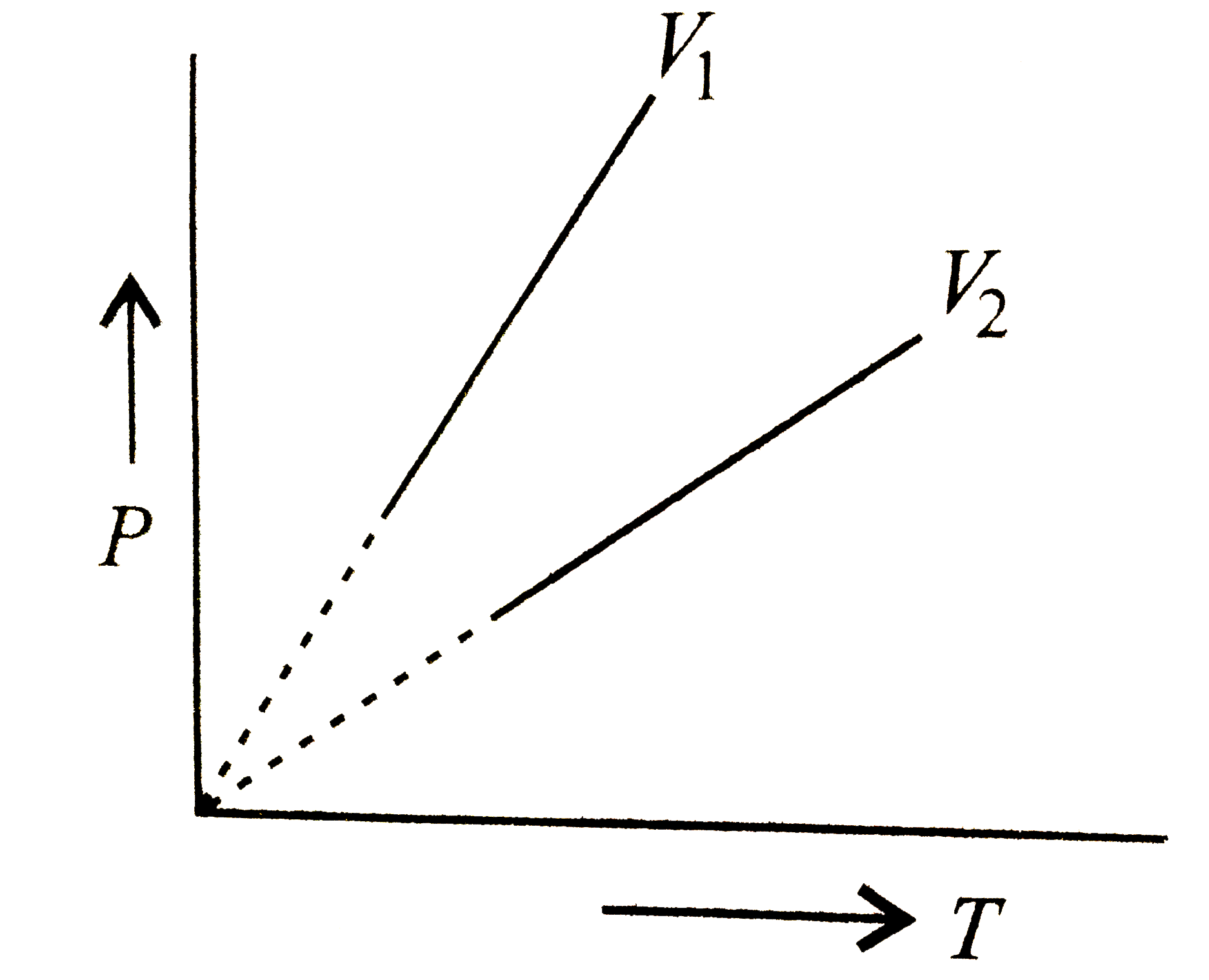
In the given pressure-temperature (P−T) diagram, what is the relation between volumes V1 and V2 for a fixed mass of a gas?
A. V1>V2
B. V2>V1
C. V1=V2
D. V2=2V1
To solve the problem regarding the relation between volumes V1 and V2 for a fixed mass of gas in a pressure-temperature (P-T) diagram, we can follow these steps:
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = universal gas constant
- T = temperature
Step 2: Analyze the P-T Diagram
In a P-T diagram, the relationship between pressure and temperature can be represented as a line or curve. The slope of this line can give us information about how pressure changes with temperature for a fixed amount of gas.
Step 3: Relate Pressure and Volume
From the ideal gas law, we can express pressure P in terms of volume V and temperature T:
P=nRV⋅T
This shows that for a fixed mass of gas (constant n and R), if we increase the volume V, the pressure P must decrease for a given temperature T.
Step 4: Compare Volumes V1 and V2
Given that the slopes of the lines in the P-T diagram are different (let's denote them as k1 and k2), we can say:
- If k2>k1, it indicates that the pressure is increasing more rapidly with temperature for the second volume V2 than for the first volume V1.
Step 5: Use the Relationship of Slopes
From the relationship of slopes:
nRV2>nRV1
This implies:
1V2>1V1
Thus, if 1V2>1V1, it follows that:
V1>V2
Conclusion
Therefore, for a fixed mass of gas, the relationship between the volumes is:
V1>V2
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = universal gas constant
- T = temperature
In a P-T diagram, the relationship between pressure and temperature can be represented as a line or curve. The slope of this line can give us information about how pressure changes with temperature for a fixed amount of gas.
From the ideal gas law, we can express pressure P in terms of volume V and temperature T:
P=nRV⋅T
This shows that for a fixed mass of gas (constant n and R), if we increase the volume V, the pressure P must decrease for a given temperature T.
Given that the slopes of the lines in the P-T diagram are different (let's denote them as k1 and k2), we can say:
- If k2>k1, it indicates that the pressure is increasing more rapidly with temperature for the second volume V2 than for the first volume V1.
From the relationship of slopes:
nRV2>nRV1
This implies:
1V2>1V1
Thus, if 1V2>1V1, it follows that:
V1>V2
Therefore, for a fixed mass of gas, the relationship between the volumes is:
V1>V2
Topper's Solved these Questions
Similar Questions
In the given (V-T) diagram, what is the relation between pressure P1andP2 ?

View SolutionIn the given (V-T) diagram, what is the relation between pressure P1andP2 ?

View SolutionIn the given (V-T) diagram, what is the relation between pressure P1andP2 ?

View SolutionThe given figure shows the pressure-temperature (P-T) diagram for a fixed mass of an ideal gas undergoing cyclic process ABCA. The corresponding pressure-volume (P-V) graph for the given cyclic process will be
_PHY_E06_003.png)
View SolutionA plot of P vs T for a given mass of gas at constant volume is a straight line . P vs T at constant volumes V1 and V2 for an ideal gas are shown below :
Which of the following is correct ?
View Solutionwhich of the following volume-temperature (V−T) curve best represents an isobaric process for a fixed mass of gas?
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and a final pressure Pi, If the same gas is expanded adiabatically to a volume 2V, the final pressure Pa. The ratio of the specific heats of the gas is 1.67. The ratio PaP1 is .......
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and a final pressure Pi, If the same gas is expanded adiabatically to a volume 2V, the final pressure Pa. The ratio of the specific heats of the gas is 1.67. The ratio PaP1 is .......
View SolutionOne mole of an ideal gas at pressure P0 and temperature T0 is expanded isothermally to twice its volume and then compressed at constant pressure to (V0/2) and the gas is brought bac to original state by a process in which PαV (pressure is directly proportional to volume). The correct temperature of the process is
View SolutionFigure shows volume - temperature (V-T) graph for same mass of an ideal gas at two different pressures P1and P2. Hence
View Solution
