The relation between acceleration and distance is is : a=(4−2x) .Select the correct alternative (s) .
Particle further comes to rest at x = 4
Particle oscillates about x = 2
Maximum speed of particle is 4 units
All of the above
The correct Answer is:A, B
To solve the problem, we need to analyze the given relation between acceleration and distance, which is expressed as:
a=4−2x
Step 1: Understanding the Relation
The first step is to understand what this equation implies. Here, a is the acceleration of the particle, and x is the distance. The equation indicates that the acceleration is dependent on the position x.
Step 2: Finding Velocity
To find the velocity of the particle, we can use the relation between acceleration and velocity. We know that:
a=vdvdx
Substituting the expression for acceleration into this equation gives:
vdvdx=4−2x
Step 3: Separating Variables
Next, we separate the variables to integrate:
vdv=(4−2x)dx
Step 4: Integrating Both Sides
Now, we integrate both sides:
∫vdv=∫(4−2x)dx
The left side integrates to:
v22
The right side integrates to:
4x−x2+C
Thus, we have:
v22=4x−x2+C
Step 5: Solving for Velocity
Multiplying through by 2 gives:
v2=8x−2x2+2C
Taking the square root:
v=±√8x−2x2+2C
Step 6: Finding Conditions for Rest
To determine if the particle comes to rest at x=4, we set v=0:
0=8(4)−2(42)+2C
This simplifies to:
0=32−32+2C⟹2C=0⟹C=0
Thus, the velocity equation simplifies to:
v=√8x−2x2
Step 7: Verifying Rest Condition
Now, substituting x=4:
v=√8(4)−2(42)=√32−32=0
This confirms that the particle comes to rest at x=4.
Step 8: Finding Maximum Speed
To find the maximum speed, we differentiate the velocity equation with respect to x and set it to zero:
dvdx=12√8x−2x2⋅(8−4x)=0
Setting the numerator to zero gives:
8−4x=0⟹x=2
Step 9: Maximum Speed Calculation
Now, substituting x=2 back into the velocity equation:
v=√8(2)−2(22)=√16−8=√8=2√2
Step 10: Conclusion
Thus, the maximum speed of the particle is 2√2, which is approximately 2.83, and not 4 units.
Final Verification
1. The particle comes to rest at x=4 (True).
2. The maximum speed is 2√2 (False).
3. The particle oscillates about x=2 (True).
Correct Alternatives
The correct alternatives are:
- The particle comes to rest at x=4.
- The particle oscillates about x=2.
The first step is to understand what this equation implies. Here, a is the acceleration of the particle, and x is the distance. The equation indicates that the acceleration is dependent on the position x.
To find the velocity of the particle, we can use the relation between acceleration and velocity. We know that:
Next, we separate the variables to integrate:
Now, we integrate both sides:
Multiplying through by 2 gives:
To determine if the particle comes to rest at x=4, we set v=0:
Now, substituting x=4:
To find the maximum speed, we differentiate the velocity equation with respect to x and set it to zero:
Now, substituting x=2 back into the velocity equation:
Thus, the maximum speed of the particle is 2√2, which is approximately 2.83, and not 4 units.
1. The particle comes to rest at x=4 (True).
2. The maximum speed is 2√2 (False).
3. The particle oscillates about x=2 (True).
The correct alternatives are:
- The particle comes to rest at x=4.
- The particle oscillates about x=2.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)19videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)14videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 175videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)1videos
JEE MAIN REVISON TEST-23
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
The correct relation between joule and erg is
A1J=10−5 ergB1J=105 ergC1J=10−7 ergD1J=107 erg
select correct statement (s)
View Solutionselect correct statement (s)
View SolutionAcceleration of a particle which is at rest at x=0 is →a=(4−2x)ˆi. Select the correct alternative (s).
View SolutionA particle moves in a straight line with constant acceleration under a constant force F. Select the correct alternative(s).
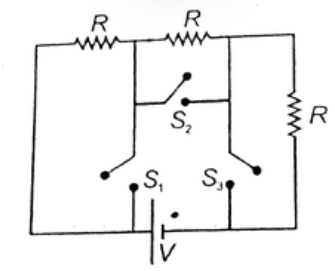
View SolutionIf all the resistors are identical , select the correct alternative (s).
 View Solution
View SolutionThe radius of a spherical ball is (10.4 ± 0.4) cm Select the correct alternative
View SolutionAn electric dipole is placed at the centre of a sphere. Select the correct alternative(s).
View Solution