Question

Find the area of the region enclosed by the parabola $y^2=4axand$
the line $y=mx\stackrel{.}{}$

Explanation

Given, curve `y^(2)=4ax " " ` …(1)
and equation of line, `y=mx " " ` …(2)

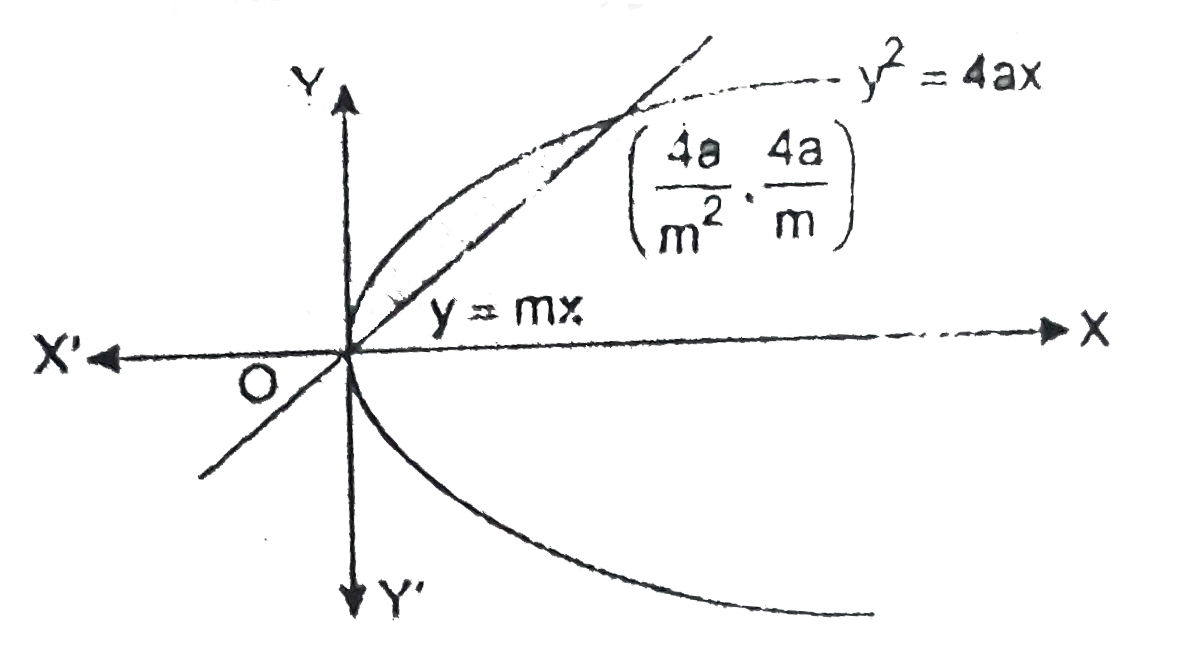
From equations (1) and (2),
`(mx)^(2)=4aximplies x(m^(2)x-4a)=0`
`implies x=0" or "x=(4a)/(m^(2))`
When, `x=0, " " y=mxx0=0`
When, `x=(4a)/(m^(2)), y=mxx(4a)/(m^(2))=(4a)/(m)`
` :. ` The points of intersection of two curves are (0, 0) and `((4a)/(m^(2)),(4a)/(m)).`
` :. ` Required area ` int_(0)^(4a//m^(2))(sqrt(4ax)-mx)dx`
`=2sqrt(a)[(x^(3//2))/(3//2)]_(0)^(4a//m^(2))-[m*(x^(2))/(2)]_(0)^(4a//m^(2))`
`=(4)/(3)sqrt(a)((4a)/(m^(2)))^(3//2)-(m)/(2)((4a)/(m^(2)))^(2)`
`=(4)/(3)sqrt(a)*((4a)/(m^(2)))sqrt((4a)/(m^(2)))-(m(16a^(2)))/(2m^(4))`
`=(32)/(3)*(a^(2))/(m^(3))-(8a^(2))/(m^(3))`
`=(8a^(2))/(3m^(3))` sq. units.