Using the method of integration find the area of the region bounded by lines:2x+y=4,3x−2y=6and x−3y+5=0
Equation of given lines are,
2x+y=4 …(1)
3x−2y=6 …(2)
x−3y+5=0 …(3)
From equations (1) and (2),
4−2x=3x−62
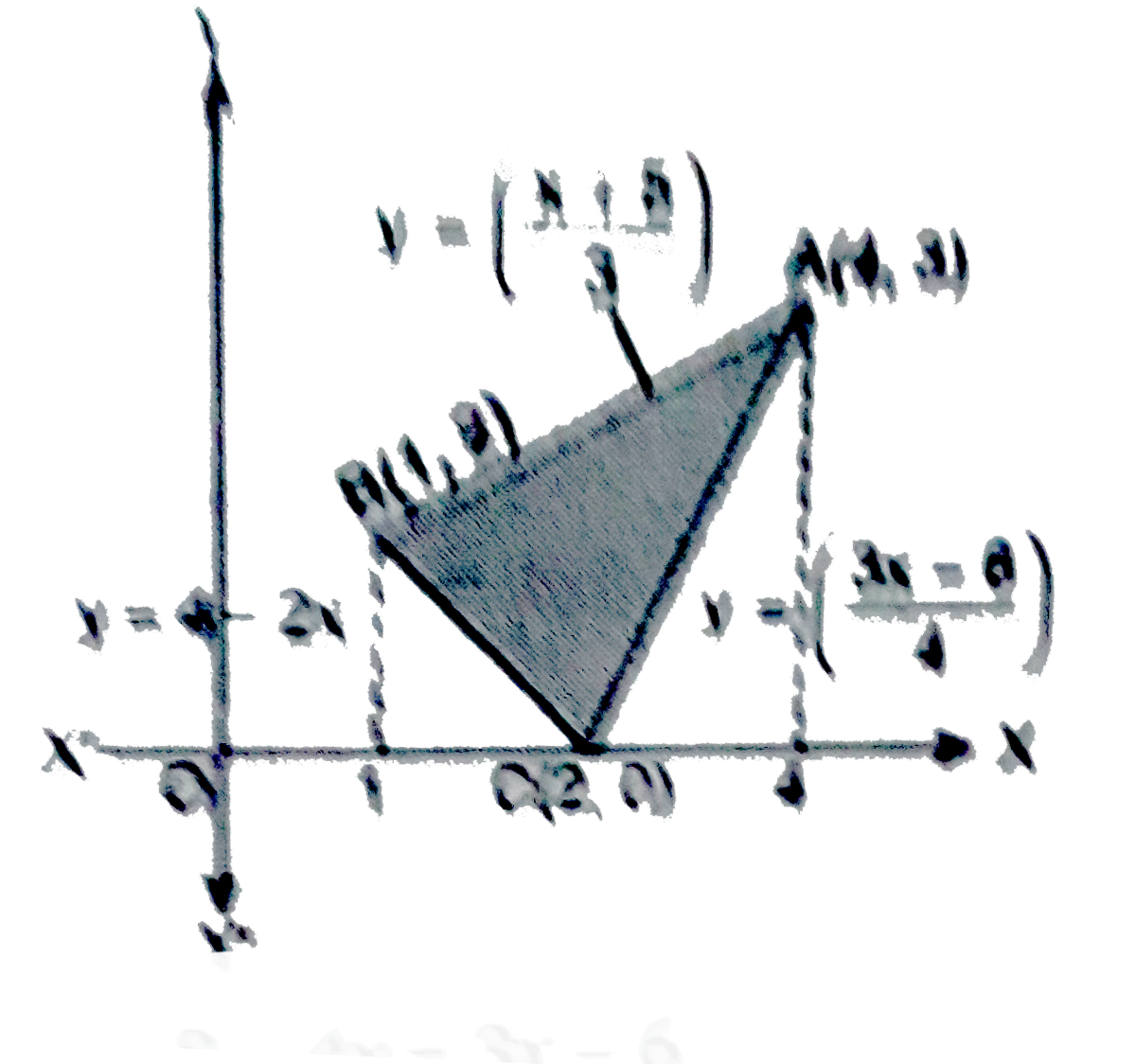
⇒8−4x=3x−6
⇒7x=14⇒x=2
From equation (1),
y=4−2x=4−2×2=0
∴ Equation (1) and (2) intersect each other at point (2, 0).
From equations (2) and (3),
3x−62=x+53⇒9x−18=2x+10
⇒7x=28⇒x=4
From equation (2), y=3×4−62=3
∴ Equation (2) and (3) intersect each other at point (4, 3).
From equations (1) and (2), 4−2x=x+53
⇒7x=7⇒x=1
From equation (1), y=4−2x=4−2×1=2
Equation (1) and (3) intersect each other at point (1, 2).
∴ Required area =∫41(x+53)dx−∫21(4−2x)dx−∫42(3x−62)dx
=13[(x+5)22]41−[4x−x2]21−12[3x22−6x]42
=16[92−62]−{(8−4)−(4−1)}−12[(3×422−6×4)−(3×222−6×2)]
=456−1−12(0−6+12)
=152−1−3=72 sq. units.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.27videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
Using the method of integration, find the area of the region bounded by the lines 3x − 2y+1=0, 2x+3y − 21=0 and x − 5y+9=0.
View SolutionUsing the method of integration, find the area of the region bounded by the following lines 3x−y−3=0,2x+y−12=0,x−2y−1=0.
View SolutionUsing the method of integration find the area bounded by the curve |x|+|y|=1.
View SolutionUsing integration, find the area of the region bounded by the curves y=x and y=x3.
View SolutionUsing integration, find the area of the region bounded by the lines y=1+|x+1|,x=−2,x=3andy=0.
View SolutionFind the area of the region bounded by the curves y=x2+2, y=x,x=0andx=3.
View SolutionFind the area of the region bounded by y=3x and the lines y = 3 and x = 0.
View SolutionUsing intergration, find the area of the region bounded by the lines y=|x+1|,x=−3,x=1 and X-axis.
View SolutionFind the area of the region bounded by y =x2+1,y=x ,x=0 and y=2
View SolutionUsing integration, find the area of the region bounded by the line 2y=5x+7 , X-axis and the line x = 2 and x = 8.
View Solution

