Question

Find the area bounded by curves $\{(x,y):y\ge x^2\text{and}y=\left|x\right|\}$

Explanation

Given parabola
`y=x^(2) " " `…(1)
and euation of line, `y=|x| " " ` …(2)
In first quadrant, equation of line y = x and in second quadrant, equation of line is y = -x and the points of intersection of parabola and lines are (-1, 1) and (1, 1).

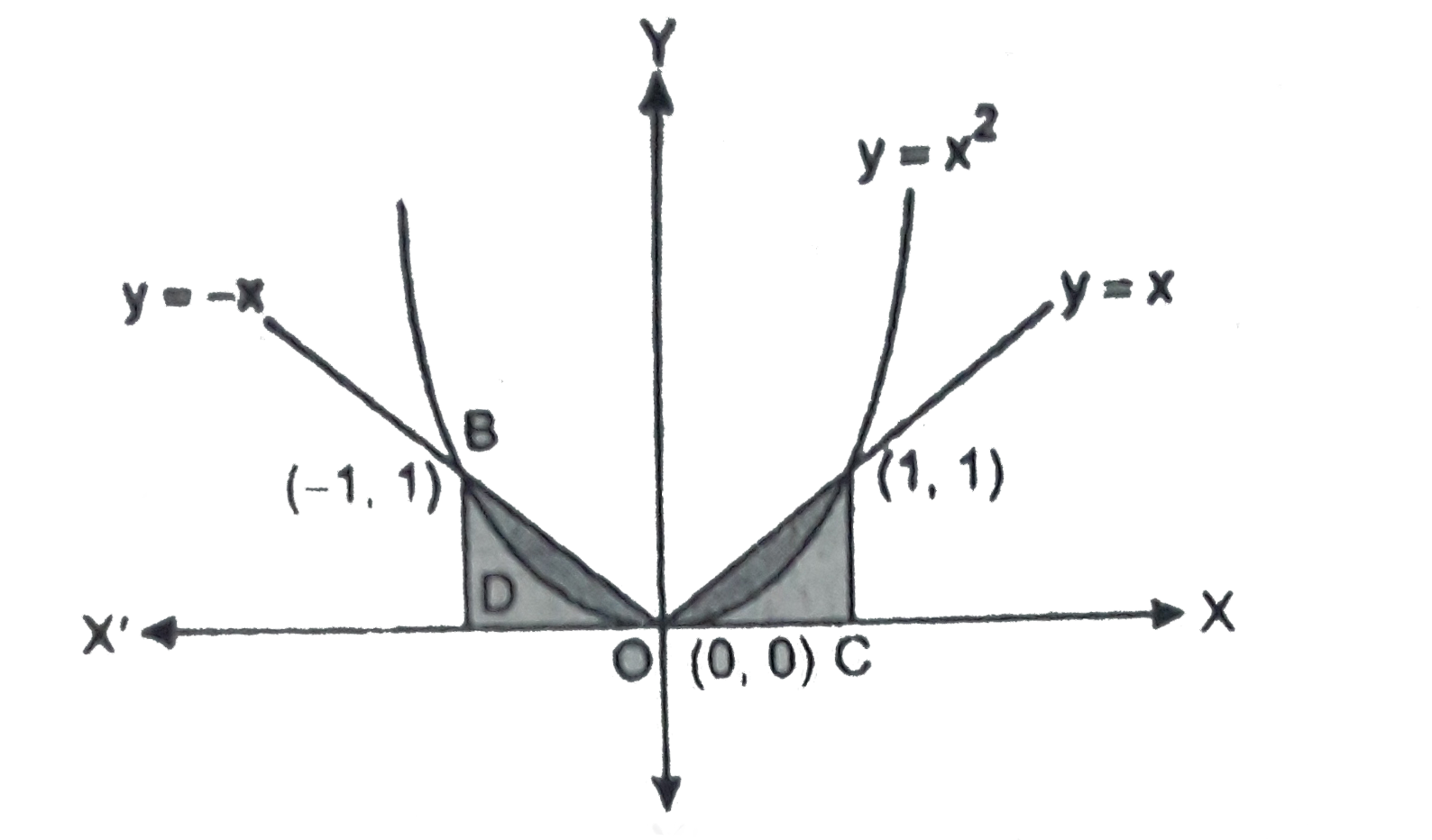
` :. ` Required area
`=2xx` (shaded area in first quadrant)
` = 2int_(0)^(1)(x-x^(2))dx=2[int_(0)^(1)xdx-int_(0)^(1)x^(2)dx]`
`=2([(x^(2))/(2)]_(0)^(1)-[(x^(3))/(3)]_(0)^(1))`
`=2[((1)/(2)-0)-((1)/(3)-0)]`
`=2[(1)/(2)-(1)/(3)]=2[(1)/(6)]=(1)/(3)` sq. units.