The area bounded by the curve y=x|x|, x-axis and the ordinates x=−1 & x=1 is:
0
13
23
43
The correct Answer is:C
Given, y=x|x|={ x2,x≥0−x2,x<0
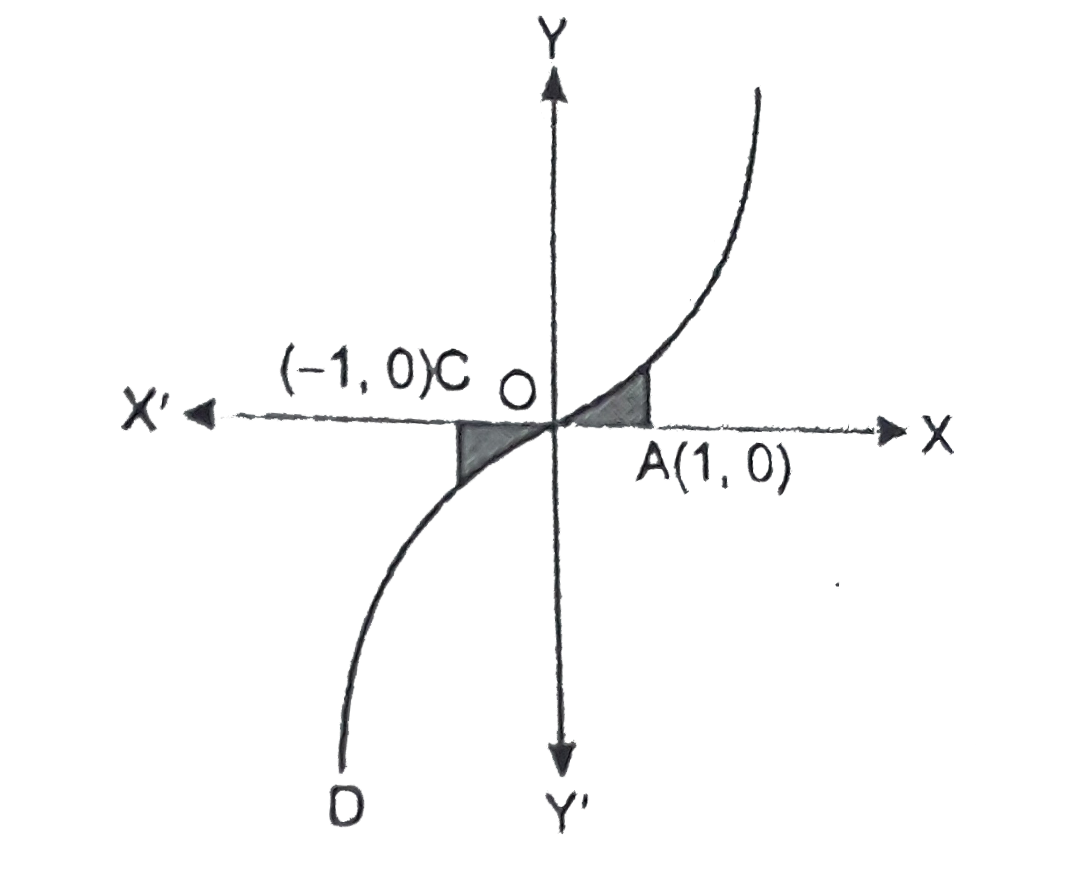
∴ Required area =2∫10x|x|=2∫10x2dx
=2[x33](0)1=23(13−03)
=23 sq. unit.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.27videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
Area bounded by the curve y=x3, the x-axis and the ordinates x=−2 and x=1 is:
View SolutionFind the area bounded by the curve y=4x−x2, the x-axis and the ordinates x=1 and x=3.
View SolutionIf the area bounded by the curve y=f(x), x-axis and the ordinates x=1 and x=b is (b-1) sin(3b+4), then find f(x).
View SolutionThe area of the region bounded by the curve y=x3, X-axis and the ordinates x = 1, x = 4 is
View SolutionFind the area bounded by the line y=x, the x-axis and the ordinates x=−1 and x=2
View SolutionFind the area bounded by the line y=x, the x-axis and the ordinates x=−1 and x=2
View SolutionThe area bounded by the curve y=sin2x, axis and y=1, is
View SolutionStatement-1: The area bounded by the curve y=xsinx, x-axis and ordinates x=0 and x=2π is 4π.Statement-2: The area bounded by the curve y=f(x), x-axis and two ordinates x=a and x=b is ∫ba|y|dx.
(A) Both 1 and 2 are true and 2 is the correct explanation of 1 (B) Both 1 and 2 are true and 2 is not correct explanation of 1 (C) 1 is true but 2 is false (D) 1 is false but 2 is trueView SolutionFind the area bounded by the curve y=cosx, x-axis and the ordinates x=0 and x=2π.
View SolutionThe area bounded by the curve y=4−x2 and X-axis is
View Solution

