Area bounded by the curve y=x3, the x-axis and the ordinates x=−2 and x=1 is:
−9
−154
154
174
The correct Answer is:D
Given curve is y=x3
If we replace x by -x and y by -y then we get y=x3.
Therefore, curve is symmetric in opposite quadrants and passes through the orgin (0, 0).
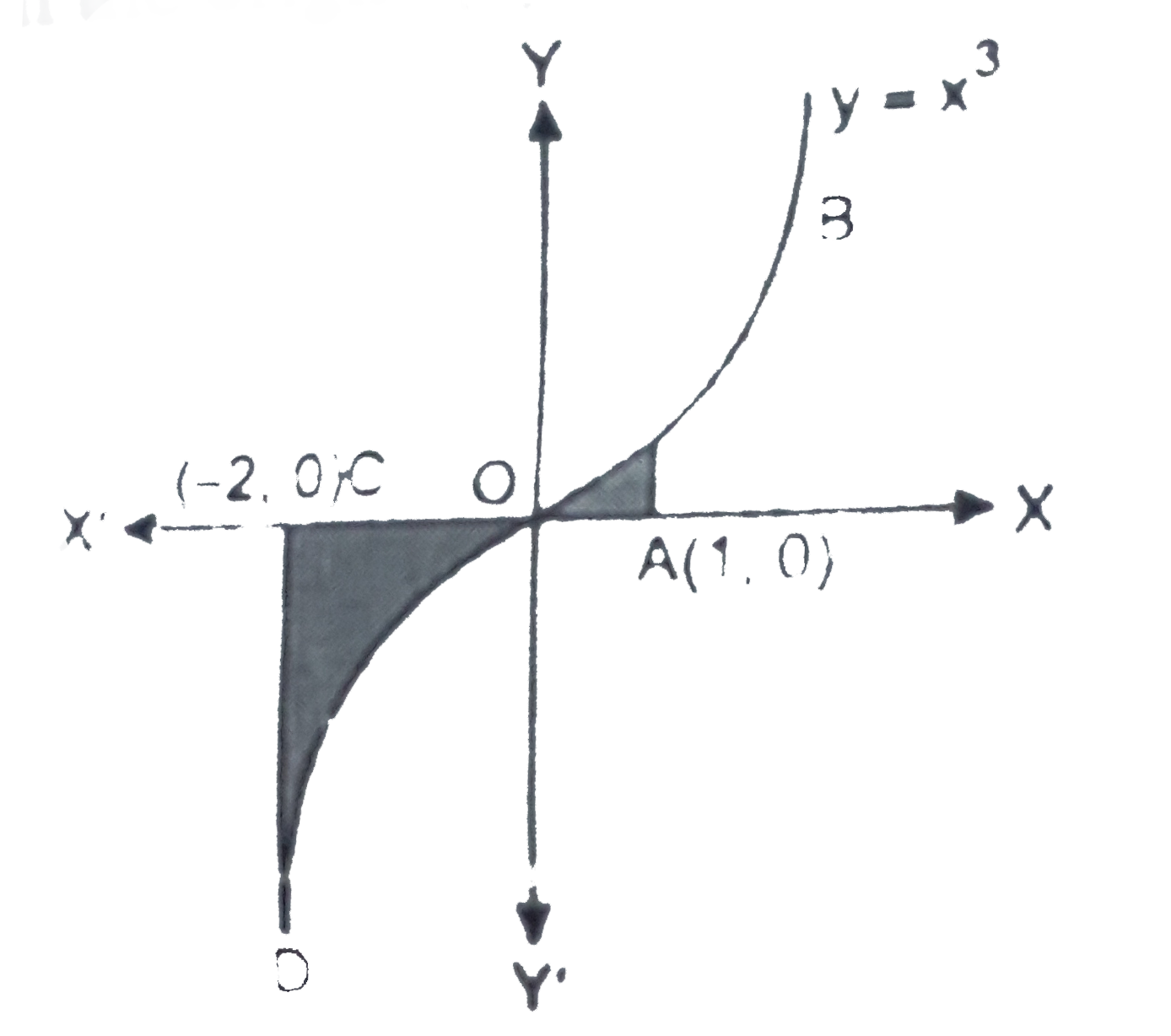
∴ Required area =∫1−2∣∣x3∣∣dx
=∫0−2∣∣x3∣∣dx+∫10∣∣x3∣∣dx
=∫0−2(−x3)dx+∫10x3dx
=−[x44]0−2+[x44]10
=−[0−(−2)44]+[14−0]
=−(−4)+(14)=174 sq. units.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.27videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
Find the area bounded by the curve y=4x−x2, the x-axis and the ordinates x=1 and x=3.
View SolutionThe area of the region bounded by the curve y=x3, X-axis and the ordinates x = 1, x = 4 is
View SolutionFind the area bounded by the line y=x, the x-axis and the ordinates x=−1 and x=2
View SolutionFind the area bounded by the line y=x, the x-axis and the ordinates x=−1 and x=2
View SolutionA point chanrge of magnitude q=4.5nC is moving with speed v=3.6×107ms−1 parallel to the x-axis along the line y=3m. Find the magnetic field at the origin produced by this charge when the charge is at the point x=−4m, y=3m, as shown in Fig.
 View Solution
View SolutionFind the area of the region bounded by the curve y=x2−2x, the x-axis and the lines x=1andx=−1
View SolutionThe area bounded by the curve y=x|x|, x-axis and the ordinates x=−1 & x=1 is:
View SolutionFind the area bounded by the curve y=cosx, x-axis and the ordinates x=0 and x=2π.
View SolutionIf the area bounded by the curve y=f(x), x-axis and the ordinates x=1 and x=b is (b-1) sin(3b+4), then find f(x).
View SolutionCalculate the area bounded by the curve y=x(3−x)2 the x-axis and the ordinates of the maximum and minimum points of the curve.
View Solution

