The area of the circle x2+y2=16exterior to the parabola y2=6xis(A) 43(4π−√3) (B) 43(4π+√3)(C) 43(8π−√3) (D) 43(8π+√3)
43(4π−√3)
43(4π+√3)
43(8π−√3)
43(8π+√3)
The correct Answer is:C
For the point of intersection of the circle x2+y2=16 and parabola y2=6x
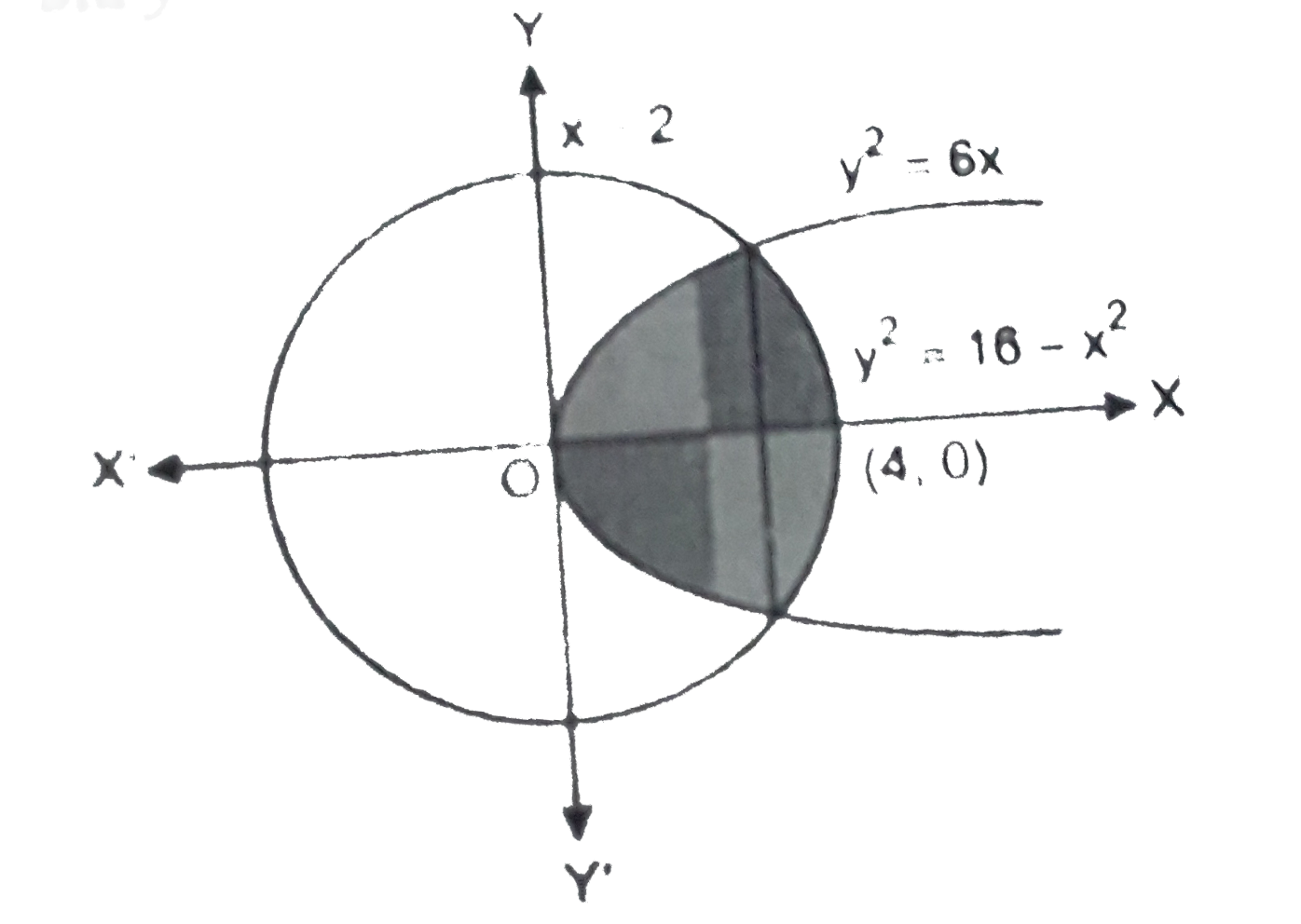
x2+6x=16
⇒x2+6x−16=0
⇒(x+8)(x−2)=0
⇒x=−8,2
∴ Required area
= area of circle −2×(area of shaded region)
=π(4)2−2[∫20√6x+∫42√16−x2dx]
=16π−2√6[x3/23/2]20−2[x2√16−x2+162sin1x4]42
=16π−4√63(23/2−0)−2[0+8sin−1(1)−√16−4−8sin−112]
=16π−4√6×2√23−2[8×π2−√12−8×π2]
=16π−16√33−16π3+4√3
=32π3−4√33
=43(8π−√3) sq. units.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.27videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
The largest value of a for which the circle x2+y2=a2 falls totally in the interior of the parabola y2=4(x+4) is 4√3 (b) 4 (c) 4√67 (d) 2√3
View SolutionThe point on the parabola y2=8x at which the normal is inclined at 60∘ to the x-axis has the co-ordinates as (a) (6,−4√3) (b) (6,4√3) (c) (−6,−4√3) (d) (−6,4√3)
View Solutionthe length of intercept made by the line √2x−y−4√2=0 on the parabola y2=4x is equal to (a) 6√3 (b) 4√3 (c) 8√2 (d) 6√2
View SolutionIf the area of a square is same as the area of the circle, then the ratio of their perimeters, in terms of π , is (a) π :√3 (b) 2 :√π (c) 3 :π (d) π :√2
View SolutionA pair of tangents is drawn to a unit circle with center at the origin and these tangents intersect at A enclosing an angle of 600 . The area enclosed by these tangents and the arc of the circle is (a) 2√3−π6 (b) √3−π3 (c) π3−√36 (d) √3(1−π6)
View SolutionThe ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal, is (a) π :√2 (b) π :√3 (c) √3 :π (d) √2 :π
View SolutionIn Fig. 15.111, if ABC is an equilateral triangle, then shaded area is equal to (FIGURE) (a) (π3−√34)r2 (b) (π3−√32)r2 (c) (π3+√34)r2 (d) (π3+√3)r2
View SolutionIf 4 cos−1x+sin−1x=π , then the value of x is (a) 32 (b) 1√2 (c) √32 (d) 2√3
View SolutionThe angle between the tangents drawn from the point (1,4) to the parabola y2=4x is (A) π6 (B) π4 (C) π3 (D) π2
View SolutionThe director circle of a hyperbola is x2+y2−4y=0. One end of the major axis is (2,0) then a focus is (a) (√3,2−√3) (b) (−√3,2+√3) (c) (√6,2−√6) (d) (−√6,2+√6)
View Solution

