A battery of emf 2 V and internal resistance r is connected in series with a resistor of through an ammeter of resistance . The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
To solve the problem step by step, we will follow these instructions:
Step 1: Draw the Circuit Diagram
The circuit consists of:
- A battery with an emf of 2 V.
- An internal resistance \( r \) of the battery.
- A resistor of \( 10 \Omega \).
- An ammeter with a resistance of \( 2 \Omega \).
- The current \( I \) flowing through the circuit is \( 50 \, \text{mA} \) or \( 0.050 \, \text{A} \).
The circuit diagram can be represented as follows:
±−−−(r)−−−−(10Ω)−−−−(2Ω)−−−−+∣|∣|±−−−−−−−−−−−−−−−−−(2V)−−−−−−−−−−−−−+
Step 2: Write Down Known Values
- Emf of the battery, \( E = 2 \, \text{V} \)
- Resistance of the external resistor, \( R_1 = 10 \, \Omega \)
- Resistance of the ammeter, \( R_2 = 2 \, \Omega \)
- Current through the circuit, \( I = 50 \, \text{mA} = 0.050 \, \text{A} \)
Step 3: Calculate Total Resistance
The total resistance \( R_{total} \) in the circuit is the sum of the internal resistance \( r \), the external resistor \( R_1 \), and the ammeter resistance \( R_2 \):
\(
R_{total} = r + R_1 + R_2 = r + 10 + 2 = r + 12 \, \Omega
\)
Step 4: Apply Ohm's Law
According to Ohm's Law, the relationship between voltage, current, and resistance is given by:
\(
V = I \cdot R
\)
In this case, the voltage across the total resistance is equal to the emf of the battery:
\(
E = I \cdot R_{total}
\)
Substituting the known values:
\(
2 = 0.050 \cdot (r + 12)
\)
Step 5: Solve for \( r \)
Now, we can solve for \( r \):
\(
2 = 0.050 \cdot (r + 12)
\)
Dividing both sides by \( 0.050 \):
\(
\frac{2}{0.050} = r + 12
\)
Calculating the left side:
\(
40 = r + 12
\)
Now, isolate \( r \):
\(
r = 40 - 12 = 28 \, \Omega
\)
Final Answer
The internal resistance \( r \) of the battery is \( 28 \, \Omega \).
---
The circuit consists of:
- A battery with an emf of 2 V.
- An internal resistance \( r \) of the battery.
- A resistor of \( 10 \Omega \).
- An ammeter with a resistance of \( 2 \Omega \).
- The current \( I \) flowing through the circuit is \( 50 \, \text{mA} \) or \( 0.050 \, \text{A} \).
- Emf of the battery, \( E = 2 \, \text{V} \)
- Resistance of the external resistor, \( R_1 = 10 \, \Omega \)
- Resistance of the ammeter, \( R_2 = 2 \, \Omega \)
- Current through the circuit, \( I = 50 \, \text{mA} = 0.050 \, \text{A} \)
The total resistance \( R_{total} \) in the circuit is the sum of the internal resistance \( r \), the external resistor \( R_1 \), and the ammeter resistance \( R_2 \):
R_{total} = r + R_1 + R_2 = r + 10 + 2 = r + 12 \, \Omega
\)
According to Ohm's Law, the relationship between voltage, current, and resistance is given by:
V = I \cdot R
\)
E = I \cdot R_{total}
\)
2 = 0.050 \cdot (r + 12)
\)
Now, we can solve for \( r \):
2 = 0.050 \cdot (r + 12)
\)
\frac{2}{0.050} = r + 12
\)
40 = r + 12
\)
r = 40 - 12 = 28 \, \Omega
\)
The internal resistance \( r \) of the battery is \( 28 \, \Omega \).
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Subjective
13 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A battery of emf 1.4V and internal resistance 2Ω is connected to a resistor of 100ω resistance through an ammeter. This resistance of the ammeter is 4/3Ω. A voltmeter has also been connected to find the potential difference across the resistor.
a. Draw the circuit diagram.
b. The ammeter reads 0.02A. What is the resistance of the voltmeter?
c. The voltmeter reads 1.1V. What is the error in the reading?
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View Solution
Knowledge Check
A battery of emf 15 V and internal resistance of 4Ω is connected to a resistor. If the current in the circuit is 2A and the circuit is closed. Resistance of the resistor and terminal voltage of the battery will be
A2.5Ω,6VB3.5Ω,6VC2.5Ω,7VD3.5Ω,7V
A cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
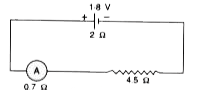
What would be the reading of the ammeter ?
View SolutionA cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the voltage drop when the current is flowing.
View Solution(A) : An ammeter is connected in series in the circuit.
(R) : An ammeter is a high resistance galvanometer.
View SolutionAn ammeter with resistance RA is connected in series with a resistor R, a battery of emf c and internal resistance r. The current measured by the ammeter is IA. Find the current through the circuit if the ammeter is removed so that the battery and the resistor form a complete circuit. Express your answer in terms of IA,r,RA and R. Show that more "ideal" the ammeter, the smaller the difference between this current and the current IA. ltbr> (b) If R=3.80Ω,ε=7.50V and r=0.45Ω, find the maximum value of the ammeter resistance RA so that IA is within 99% of the current in the circuit when the ammeter is absent. (c) Explain why your answer in part (b) represents a maximum value.
View SolutionThree identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current through the battery,
View SolutionA cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the p.d. across each resistor
View Solution
