A capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the initial charge on the charged capacitor
The initial charge Q on the charged capacitor can be calculated using the formula:
Q=C×V
Where:
- C=5μF=5×10−6F
- V=20V
Calculating Q:
Q=5×10−6F×20V=100×10−6C=100μC
Step 2: Determine the new configuration after connecting the uncharged capacitor
When the uncharged capacitor is connected in parallel, the total charge Q will distribute equally between the two capacitors. Since the capacitors are in parallel, they will have the same potential difference across them.
Let the capacitance of the uncharged capacitor also be C=5μF. After connecting, the total capacitance Ceq becomes:
Ceq=C1+C2=5μF+5μF=10μF
Step 3: Calculate the new voltage across the capacitors
The total charge remains the same, which is 100μC. The voltage VAB across the equivalent capacitance can be calculated using:
VAB=QCeq=100×10−6C10×10−6F=10V
Step 4: Calculate the total energy stored in the capacitors
The energy U stored in a capacitor is given by the formula:
U=12CV2
Using the equivalent capacitance and the voltage across it:
U=12×Ceq×V2AB
Substituting the values:
U=12×10×10−6F×(10V)2
Calculating the energy:
U=12×10×10−6×100=500×10−6J=500μJ
Final Answer
The total energy stored in the capacitors is 500μJ.
---
The initial charge Q on the charged capacitor can be calculated using the formula:
Q=C×V
Where:
- C=5μF=5×10−6F
- V=20V
Q=5×10−6F×20V=100×10−6C=100μC
When the uncharged capacitor is connected in parallel, the total charge Q will distribute equally between the two capacitors. Since the capacitors are in parallel, they will have the same potential difference across them.
Ceq=C1+C2=5μF+5μF=10μF
The total charge remains the same, which is 100μC. The voltage VAB across the equivalent capacitance can be calculated using:
VAB=QCeq=100×10−6C10×10−6F=10V
The energy U stored in a capacitor is given by the formula:
U=12CV2
Using the equivalent capacitance and the voltage across it:
U=12×Ceq×V2AB
Substituting the values:
U=12×10×10−6F×(10V)2
Calculating the energy:
U=12×10×10−6×100=500×10−6J=500μJ
The total energy stored in the capacitors is 500μJ.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Find the charge stored in the capacitor.
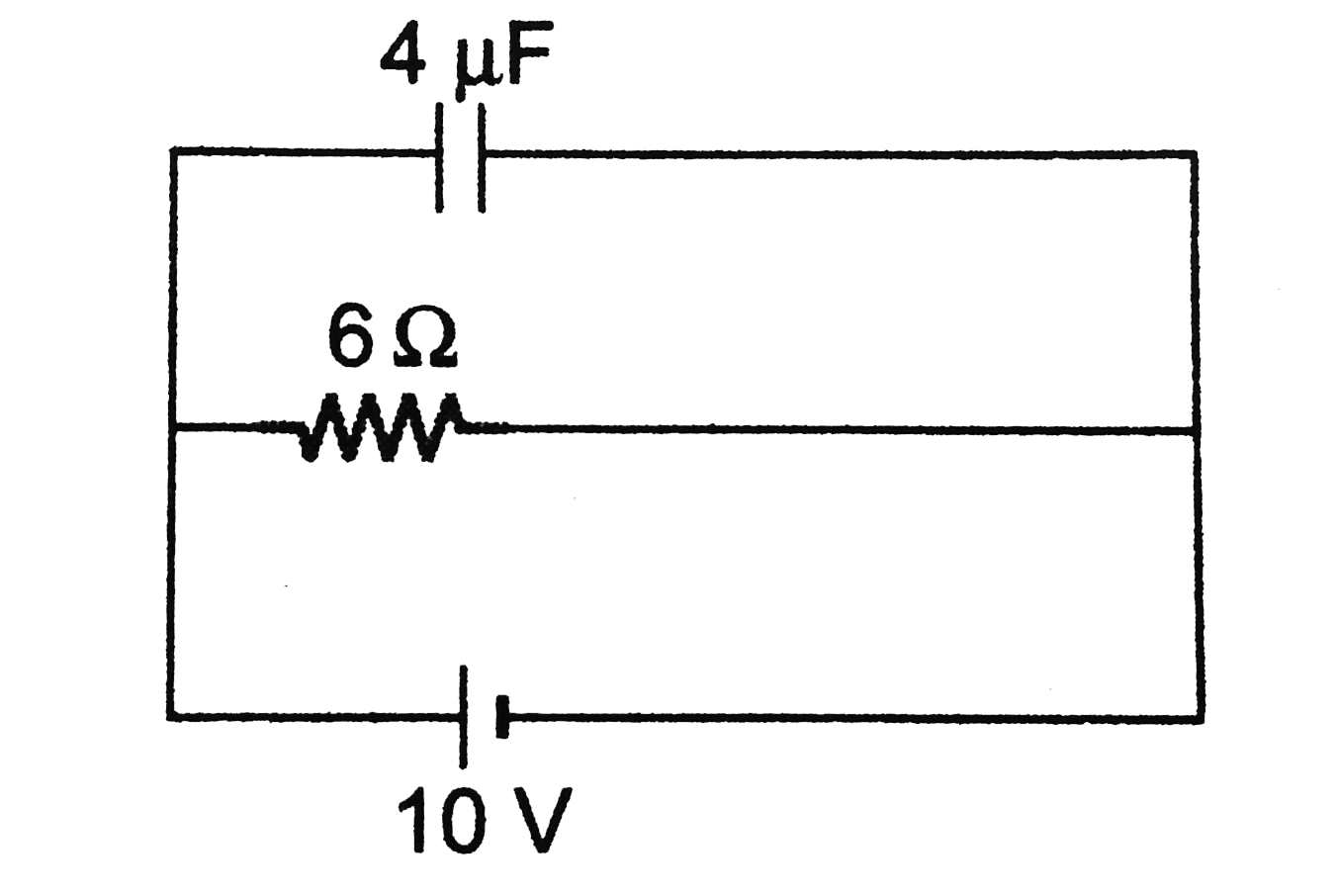
View SolutionFind the charge stored in the capacitor.
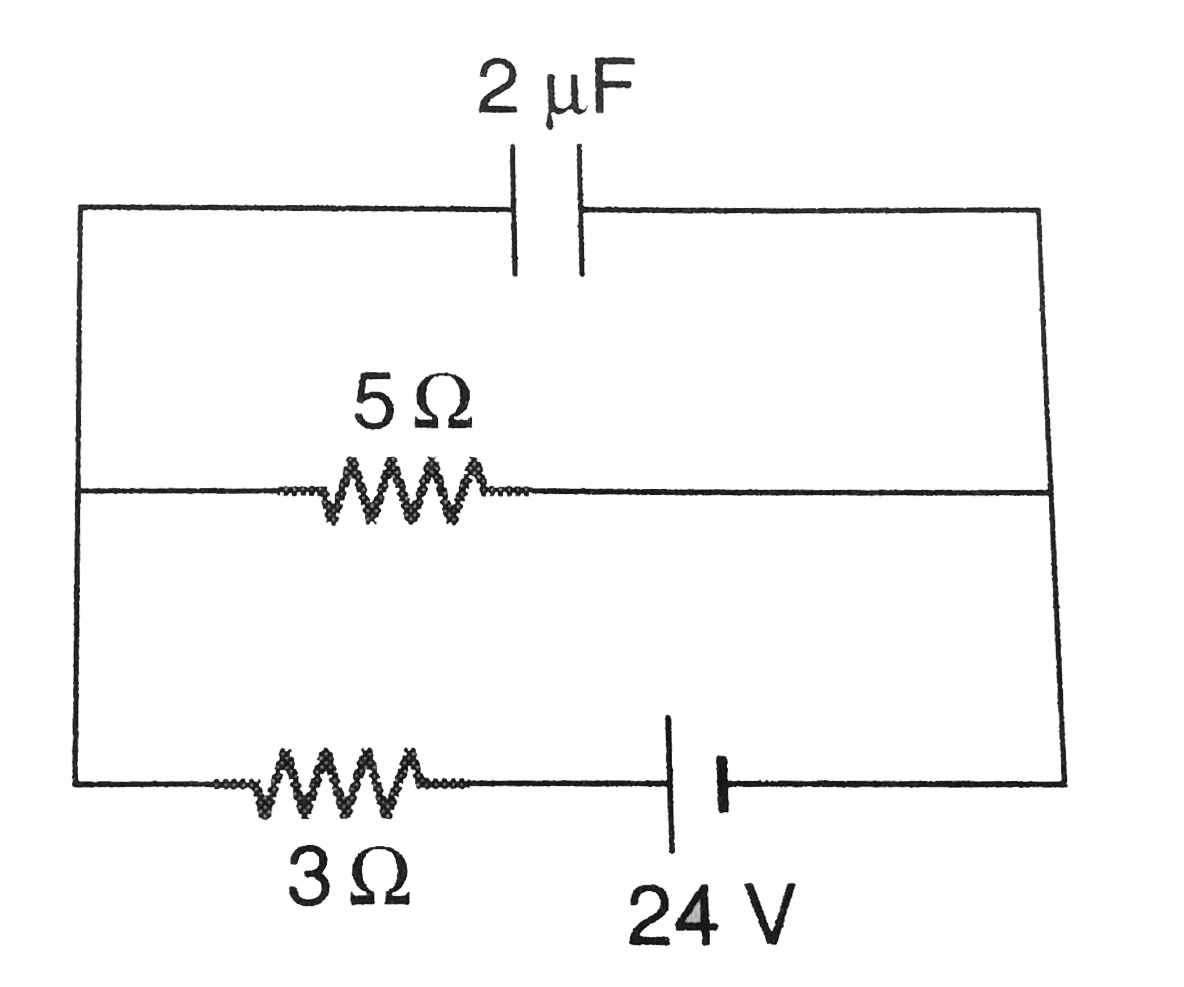
View SolutionFind the charge stored in the capacitor.
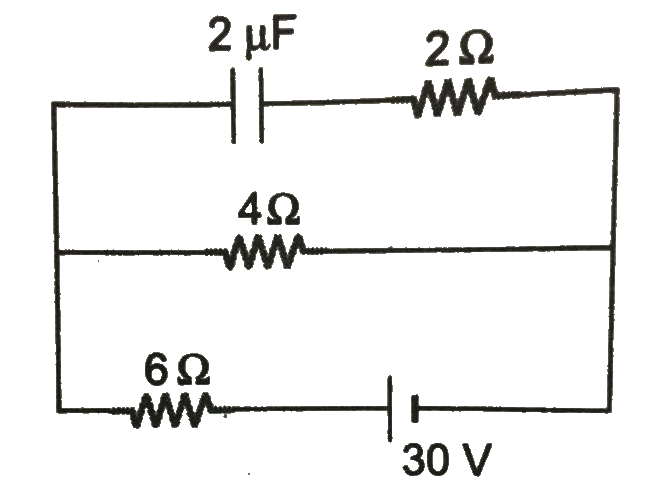
View SolutionA battery of 10V is connected to a capacitor of capacity 0.lF. The battery is now removed and this capacitor is connected to a second uncharged capacitor. If the charges are distributed equally on these two capacitors, find the total energy stored in the two capacitors. Find the ratio of final energy to initial energy stored in capacitors.
View SolutionA capacitor is charge until it stores an energy of 1J. A second uncharged capacitor is connected to it, so that charge districutes equally. The final energy stored in the second capacitor is
View SolutionA capacitor of capacity 2μF is charged to 100V. What is the heat generated when this capacitor is connected in parallel to an another capacitor of same capacity?
View SolutionA capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
View SolutionA capacitor of capacitor of capacitance 2.0μF is charge to a potential diffrence of 12V It is then connected of uncharged capacitor of capacitance 4.0μF as shown in figure . Find (a ) the charge on each of the two capacitors after the connection, (b ) the electrostatic energy stored in each of the two capacitors.

View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionA capacitor of 5μF is charged to a potential of 100V. Now, this charged capacitor is connected to a battery of 100V with the posiitive terminal of the battery connected to to the negative plate of the capacitor . For the given situation, mark the correct statement(s).
View Solution
