A cell supplies a current i1 trhough a resistnace R1 and a current i2 through a resistance R2. The internal resistance of this cell is
R2−R1
i1R2−i2R1i1−i2
i2R2−i1R1i1−i2
(i1+i2i1−i2)√R1R2
The correct Answer is:C
To find the internal resistance of the cell, we can start by using the relationships given for the currents i1 and i2 through the resistances R1 and R2 respectively.
1. Understand the circuit configuration:
- When the cell with EMF E is connected to resistance R1, the total resistance in the circuit is R1+r (where r is the internal resistance of the cell).
- The current flowing through this circuit is given as i1.
2. Write the equation for the first circuit:
i1=ER1+r
Rearranging gives:
E=i1(R1+r)
This is our Equation (1).
3. Repeat for the second circuit:
- When the same cell is connected to resistance R2, the current flowing through this circuit is i2.
i2=ER2+r
Rearranging gives:
E=i2(R2+r)
This is our Equation (2).
4. Set the two expressions for E equal:
Since both equations represent the same EMF E, we can set them equal to each other:
i1(R1+r)=i2(R2+r)
5. Expand and rearrange:
Expanding both sides gives:
i1R1+i1r=i2R2+i2r
Rearranging terms to isolate r:
i1R1−i2R2=i2r−i1r
i1R1−i2R2=r(i2−i1)
6. Solve for the internal resistance r:
Dividing both sides by (i2−i1):
r=i1R1−i2R2i2−i1
Final Answer:
The internal resistance of the cell is given by:
r=i1R1−i2R2i2−i1
- When the cell with EMF E is connected to resistance R1, the total resistance in the circuit is R1+r (where r is the internal resistance of the cell).
- The current flowing through this circuit is given as i1.
i1=ER1+r
Rearranging gives:
E=i1(R1+r)
This is our Equation (1).
- When the same cell is connected to resistance R2, the current flowing through this circuit is i2.
i2=ER2+r
Rearranging gives:
E=i2(R2+r)
This is our Equation (2).
Since both equations represent the same EMF E, we can set them equal to each other:
i1(R1+r)=i2(R2+r)
Expanding both sides gives:
i1R1+i1r=i2R2+i2r
Rearranging terms to isolate r:
i1R1−i2R2=i2r−i1r
i1R1−i2R2=r(i2−i1)
Dividing both sides by (i2−i1):
r=i1R1−i2R2i2−i1
The internal resistance of the cell is given by:
r=i1R1−i2R2i2−i1
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason18videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns4videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point70videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A cell sends a current through a resistance R1 for time t, next the same cell sends current through another resistance R2 for the time t If the same amount of heat is developed in both the resistance then find the internal resistance of the cell
View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionWhen a celll is connected to an external resistance R1, current through it is i1. When the same cell is connected to an external resistance R2, current through it is i2. Calculate the emf and internal resisance of the cell.
View SolutionA cell supplies a current of 2A to an exertnal resistance of 2Ω and a current of 1 ampere to another external resistance of 4.5Ω connected across the cell separately . Select the correct alternative (s).
View SolutionBy a cell a current of 0.9 A flows through 2 ohm resistor and 0.3A through 7 ohm resistor. The internal resistance of the cell is
View SolutionA power supply of fixed emf E is connected to a variable resistor (resistance = R) and an ammeter of resistance RA. The internal resistance of supply is r. The potential difference between the terminals of the power supply in closed circuits is denoted by V and current in circuit denoted by I. A graph is obtained between V and I by drawing varying amount of current from the supply. The correct V−I graph for the given situation is
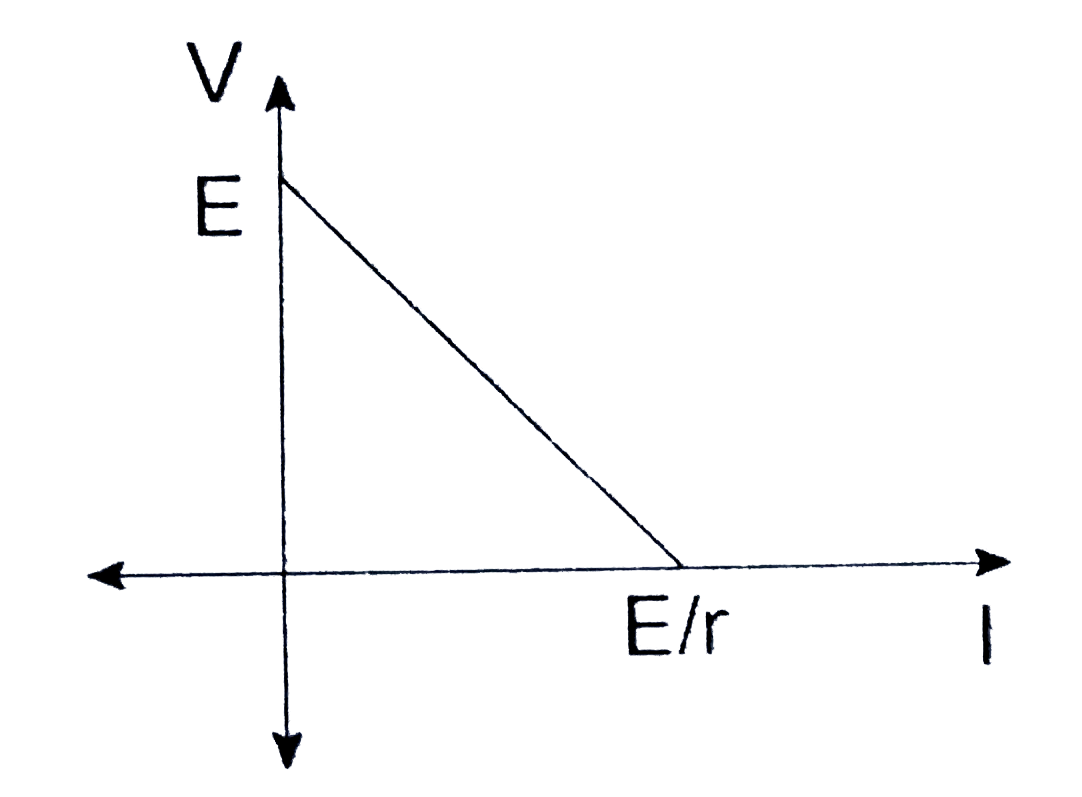
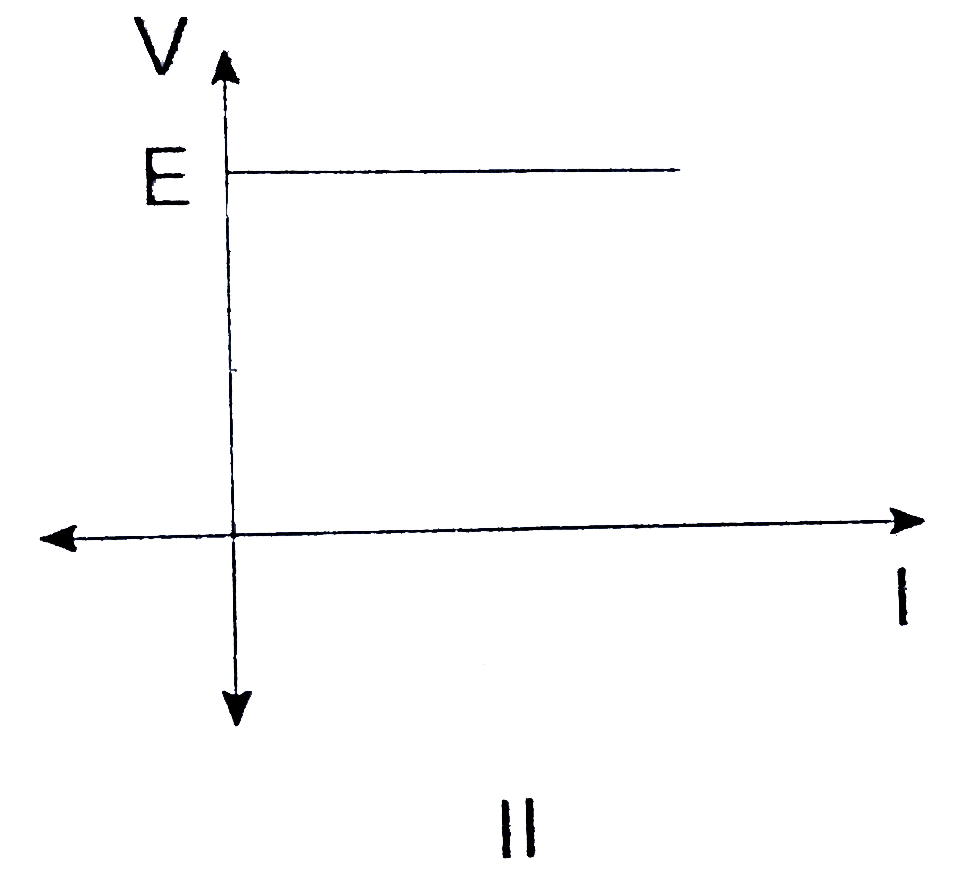
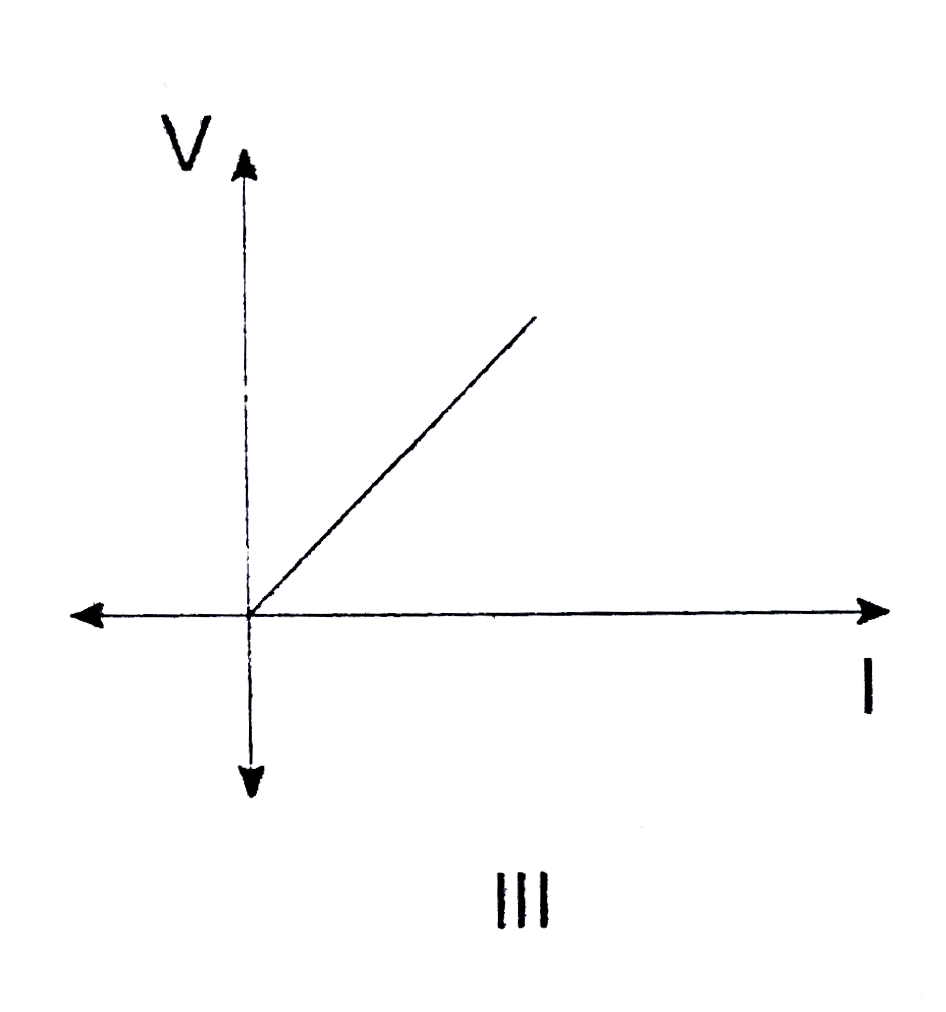
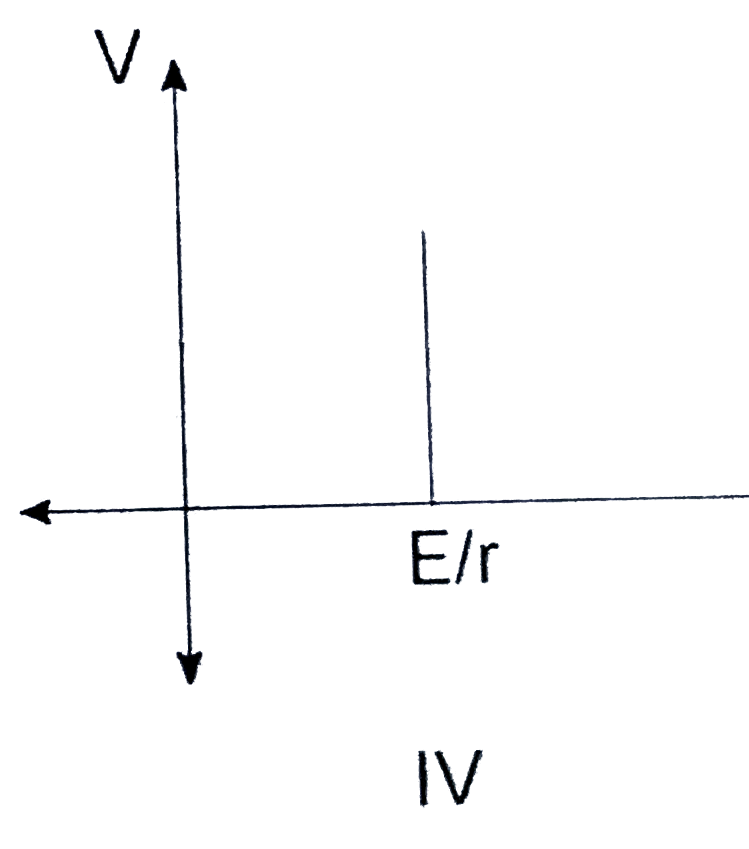 View Solution
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris
 View Solution
View SolutionIn a mixed grouping of identical cells, five rows are connected in parallel and each row contains 10 cells. This combination sends a current I through an external resistance of 20Ω. if the emf and internal resistance of each cell is 1.5 V and 1Ω, respectively then find the value of I.
View SolutionA cell of emf ε and internal resistance r drives a current i through an extermal resistance R
(i) The cell suppllied εi power
(ii) Heat is produced in R at the rate εi
(iii) Heat is produced in R at the rate εI(RR+r)
(iv) Heat is produced in the cell at the rate εi(rR+r)View Solution

