A charged particle of mass m=1 kg and charge q=2μC is thrown for a horizotal ground at an angle θ=45∘ with speed 20m/s. In space a horizontal electric field E=2×107 V/m exist. Find the range on horizontal ground of the projectile thrown.
The correct Answer is:B
To solve the problem of finding the range of a charged particle thrown at an angle with a horizontal electric field present, we will follow these steps:
Step 1: Determine the initial velocity components
The initial velocity u of the particle is given as 20m/s and the angle θ is 45∘.
- The horizontal component of the initial velocity ux is:
ux=ucosθ=20cos45∘=20×1√2=10√2m/s
- The vertical component of the initial velocity uy is:
uy=usinθ=20sin45∘=20×1√2=10√2m/s
Step 2: Calculate the time of flight
The time of flight T for a projectile is given by the formula:
T=2uyg
where g is the acceleration due to gravity (approximately 9.81m/s2).
Substituting the values:
T=2×10√29.81≈20√29.81≈2.86s
Step 3: Calculate the force due to the electric field
The force F acting on the charged particle in the horizontal direction due to the electric field E is given by:
F=qE
where q=2μC=2×10−6C and E=2×107V/m.
Calculating the force:
F=(2×10−6)×(2×107)=40N
Step 4: Calculate the horizontal acceleration
Using Newton's second law, the acceleration a in the horizontal direction is:
a=Fm
where m=1kg.
Substituting the values:
a=401=40m/s2
Step 5: Calculate the horizontal range
The range R can be calculated using the formula:
R=uxT+12aT2
Substituting the values:
R=(10√2)(2.86)+12(40)(2.86)2
Calculating R:
1. Calculate 10√2×2.86:
10√2≈14.14⇒14.14×2.86≈40.4
2. Calculate 12×40×(2.86)2:
(2.86)2≈8.18⇒12×40×8.18≈163.6
Adding both parts together:
R≈40.4+163.6=204m
Final Answer
The range of the projectile on the horizontal ground is approximately 204m.
---
The initial velocity u of the particle is given as 20m/s and the angle θ is 45∘.
ux=ucosθ=20cos45∘=20×1√2=10√2m/s
uy=usinθ=20sin45∘=20×1√2=10√2m/s
The time of flight T for a projectile is given by the formula:
T=2uyg
where g is the acceleration due to gravity (approximately 9.81m/s2).
T=2×10√29.81≈20√29.81≈2.86s
The force F acting on the charged particle in the horizontal direction due to the electric field E is given by:
F=qE
where q=2μC=2×10−6C and E=2×107V/m.
F=(2×10−6)×(2×107)=40N
Using Newton's second law, the acceleration a in the horizontal direction is:
a=Fm
where m=1kg.
a=401=40m/s2
The range R can be calculated using the formula:
R=uxT+12aT2
R=(10√2)(2.86)+12(40)(2.86)2
Calculating R:
1. Calculate 10√2×2.86:
10√2≈14.14⇒14.14×2.86≈40.4
2. Calculate 12×40×(2.86)2:
(2.86)2≈8.18⇒12×40×8.18≈163.6
R≈40.4+163.6=204m
The range of the projectile on the horizontal ground is approximately 204m.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A charged particle of mass m=1 kg and charge q=2μC is thrown from a horizontal ground at an angle θ=45∘ with the speed 25m/s. In space, a horizontal electric field E=2×107 V/m exists in the direction of motion. Find the range on horizontal ground of the projectile thrown. Take g=10m/s2.
View SolutionA charged particle of mass m = 2 kg and charge 1μC is projected from a horizontal ground at an angle θ=45∘ with speed 10ms−1. In space, a horizontal electric field towards the direction of projection E=2×107NC−1 exists. The range of the projectile is
View Solution
Knowledge Check
A particle of mass 10−3kg and charge 5μC is thrown at a speed of 20ms−1 against a uniform electric field of strength 2×105NC−1. The distance travelled by particle before coming to rest is
A0.1 mB0.2 mC0.3 mD0.4 m
A particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
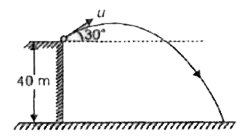
View SolutionFigure shows a projectile thrown with speed u = 20 m/s at an angle 30∘ with horizontal from the top of a building 40 m high. Then the horizontal range of projectile is
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.

View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View Solutiona projectile is thrown with speed u into air from a point on the horizontal ground at an angle θ with horizontal. If the air exerts a constant horizontal resistive force on the projectill then select correct alternative(s).
View SolutionA particle of mass m and charge q is thrown at a speed u against a uniform electric field E. How much distance will it travel before coming to momentary rest?
View Solution
