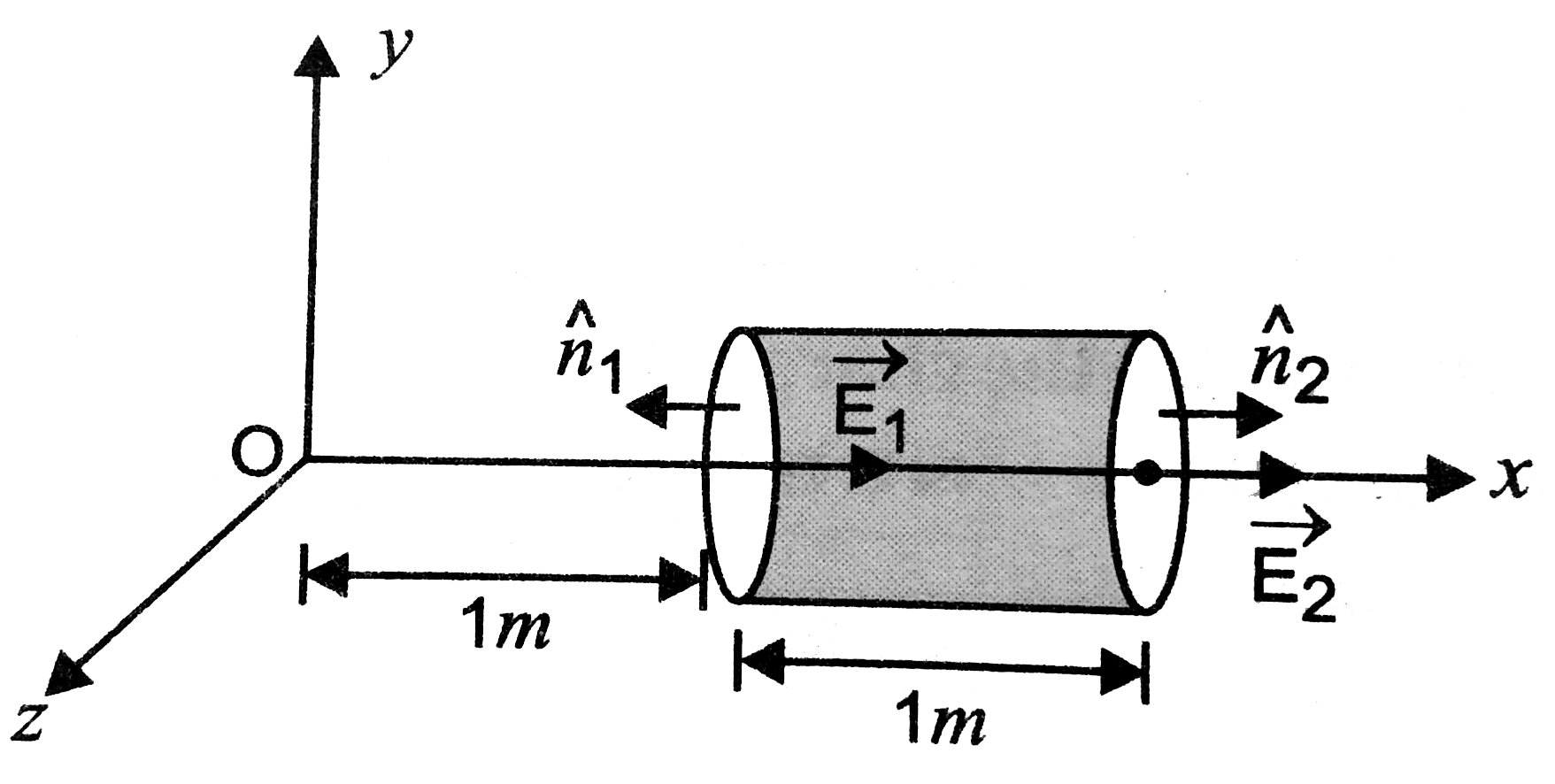
A hollow cylindrical box of length 1m area of cross-section 25cm2 is placed in a three dimensional coordinate system as shown in the electric field in the region is given
by →E=50xˆi,where E is in NC−1 and x is in metres . Find
(i) Net flux through the cylinder.
(ii) charge enclosed by the cylinder.
(##U_LIK_SP_PHY_XII_C01_E10_019_Q01.png" width="80%">
As electric field →E=50xˆINC−1 is along +ve direction of X - axis, hence flux passing through side faces 1 and 2 of cylinder is ϕ1=E1 A inward and ϕ2=E2 A outward . However , there is no flux associated with curved surface of cylinder.
∴ ϕ1=−E1A=−(50×1)×25×10−4Nm2C−1=−0.125Nm2C−1
and ϕ2=+E2A=+(50×2)×25×10−4Nm2C−1=+0.250Nm2C−1
∴ Net electric flux through cylinder
ϕ∈=ϕ1+ϕ2=−0.125+0.250=+0.125Nm2C−1
(b) As net flux f∈=q∈0,hence charge enclosed by the cylinder will be
q=∈0.Φ∈=(8.85×10−12)×0.125=1.1×10−12C=1.1pC
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - LONG ANSWER QUESTIONS -II
9 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-A)
5 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SHORT ANSWER QUESTIONS
29 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SELF ASSESSMENT TEST SECTION-C (VERY SHORT ANSWER QUESTIONS)
3 Videos
- ELECTROMAGNETIC WAVESBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SELF ASSESSMENT TEST (SECTION C)
1 Videos
Similar Questions
A bollow cylindrical box of length 1m and area of cross section 25cm2 is placed in a three dimensional co-ordinate system as shown in Fig, The electric field in the
region is given by →E=50xˆi , where E is in NC−1 and x is in meter. Find
(i) Net flux through the cylinder
(ii) Charge enclosed by the cylinder.
View SolutionA hollow cylindrical box of length 0.5m and area of cross-section 20cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by →E=20xˆi, where E is NC−1 and x is in meters, Find

(i) Net flux through the cylinder.
(ii) Charge enclosed in the cylinder.
View Solution
Knowledge Check
A hollow cylindrical box of length 1m and area of cross section 25cm2 is placed in a three dimensional co-ordinate system as shown in Fig, The electric field in the
region is given by →E=50xˆi , where E is in NC−1 and x is in meter. Find
(i) Net flux through the cylinder
(ii) Charge enclosed by the cylinder.
 A(i) 0.625Nm2/C , (ii) 3.506×10−12CB(i) 0.125Nm2/C , (ii) 1.106×10−12CC(i) 0.330Nm2/C , (ii) 2.550×10−12CD(i) 2.125Nm2/C , (ii) 6.106×10−12C
A(i) 0.625Nm2/C , (ii) 3.506×10−12CB(i) 0.125Nm2/C , (ii) 1.106×10−12CC(i) 0.330Nm2/C , (ii) 2.550×10−12CD(i) 2.125Nm2/C , (ii) 6.106×10−12CThe electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side l parallel to y-z plane.
Aal3Bal2Cal4Dal
A hollow cylindrical box of length 0.5m and area of cross-section 20cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by →E=20xˆi, where E is NC−1 and x is in meters, Find

(i) Net flux through the cylinder.
(ii) Charge enclosed in the cylinder.
View SolutionThe electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side I parallel to y-z plane.
View SolutionThe electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side I parallel to y-z plane.
View SolutionThe electric field in a region is given by →E=(Ax+B)ˆi Where E is in NC− and x is in metres. The values of constants are A=20SI Unit and B==10SI unit. If the potential at x=1 is V1 and that at x=−5 is V2 then V1−V2 is:
View SolutionA cube of side 20 cm is kept in a region as shown in the figure. An electric field →E exists in the region such that the potential at a point is given by V=10x+5, where V is in volt and x is in m.
Find the
(i) electric field →E, and
(ii) total electric flux through the cube.
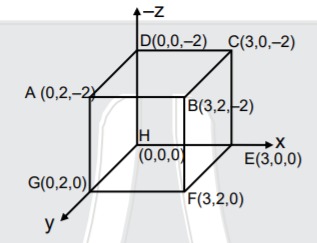
View SolutionIf electric field in the space is given by, →E=4xˆi+(y2+1)ˆj and electric flux through ABCD is ϕ1 and electric flux through BCEF is ϕ2, then find (ϕ1−ϕ2)
View Solution
