A lift moving with a uniform velocity v in which a block of mass m is lying .The friction force offered by the when coefficient of friction is μ=0.5 will be
zero
mg/2
mg
2mg
The correct Answer is:a
To solve the problem, we need to analyze the forces acting on the block of mass m in the lift that is moving with a uniform velocity v.
Step 1: Understand the scenario
The lift is moving with a uniform velocity v. This means that it is not accelerating. In this case, the block of mass m is at rest relative to the lift.
Hint: Remember that uniform velocity implies no net acceleration.
Step 2: Identify the forces acting on the block
The forces acting on the block are:
- The gravitational force acting downwards, which is mg (where g is the acceleration due to gravity).
- The normal force N acting upwards from the surface of the lift.
Hint: Draw a free-body diagram to visualize the forces acting on the block.
Step 3: Determine the normal force
Since the lift is moving with uniform velocity, the normal force N will balance the gravitational force. Therefore, we have:
\( N = mg \)
Hint: Use Newton's first law to understand that the net force in the vertical direction must be zero for the block to remain at rest.
Step 4: Calculate the maximum static friction
The maximum static friction force can be calculated using the coefficient of friction μ:
\( f_{\text{max}} = \mu N \)
Substituting the value of N:
\( f_{\text{max}} = \mu (mg) \)
Given that μ=0.5, we have:
\( f_{\text{max}} = 0.5 \times mg \)
Hint: Remember that static friction adjusts to prevent relative motion up to its maximum value.
Step 5: Analyze the motion of the block
Since the lift is moving uniformly, there is no external force trying to move the block relative to the lift. Therefore, there is no tendency for the block to slide.
Hint: Consider what happens when there is no applied force on the block.
Step 6: Conclusion about the friction force
Since there is no tendency of relative motion between the block and the lift, the actual friction force acting on the block is zero:
\( f = 0 \)
Hint: Recall that static friction only acts when there is an attempt to move the object.
Final Answer
The friction force offered by the surface when the coefficient of friction is μ=0.5 will be 0 N.
---
The lift is moving with a uniform velocity v. This means that it is not accelerating. In this case, the block of mass m is at rest relative to the lift.
The forces acting on the block are:
- The gravitational force acting downwards, which is mg (where g is the acceleration due to gravity).
- The normal force N acting upwards from the surface of the lift.
Since the lift is moving with uniform velocity, the normal force N will balance the gravitational force. Therefore, we have:
\( N = mg \)
The maximum static friction force can be calculated using the coefficient of friction μ:
\( f_{\text{max}} = \mu N \)
Substituting the value of N:
\( f_{\text{max}} = \mu (mg) \)
Given that μ=0.5, we have:
\( f_{\text{max}} = 0.5 \times mg \)
Since the lift is moving uniformly, there is no external force trying to move the block relative to the lift. Therefore, there is no tendency for the block to slide.
Since there is no tendency of relative motion between the block and the lift, the actual friction force acting on the block is zero:
\( f = 0 \)
The friction force offered by the surface when the coefficient of friction is μ=0.5 will be 0 N.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A small block of mass m is kept on a rough inclined surface of inclination θ fixed in a car. The car moves with a uniform velocity v and the block does not slide on the wedge. The work done by the force of friction on the block in time t will be
_PHY_E05_250_Q01.png)
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA lift is moving downwards with an acceleration equal to g. A block of mass m , kept on the floor of the lift of friction coefficient μ , is pulled horizontally . The friction acting on the block is
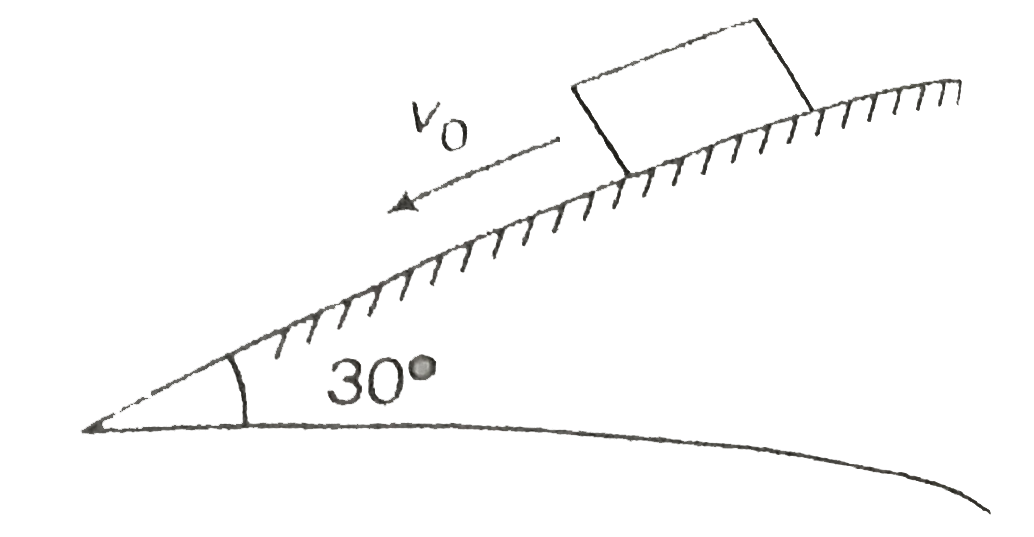
View SolutionA block of mass m is given an initial downward velocity v0 and left on inclined place ( coefficient of friction =0.6). The block will
View SolutionFind value of pulling force F for which block just moves. Given coefficient of friction for surface is μ.
View SolutionA block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0+ax. Find the kinetic energy of the block as function of x before it comes to rest.
View SolutionA skater of mass m standing on ice throws a stone of mass M with a velocity of v in a horizontal direction. The distance over which the skater will move back (the coefficient of friction between the skater and the ice is μ)
View SolutionFind the minimum force required to keep a block of mass m in equilibrium on a rough inclined plane with inclination α and coefficient of friction μ(<tanα).
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
View Solution
