A particle is acted upon by only a conservative force F=(7ˆi−6ˆj) N (no other force is acting on the particle). Under the influence of this force particle moves from (0, 0) to (-3m, 4m) then
work done by the force is 3 J
work done by the force is −45J
at (0, 0) speed of the particle must be zero
at (0, 0) speed of the particle must not be zero
The correct Answer is:B, D
To solve the problem step by step, we need to calculate the work done by the conservative force as the particle moves from the initial position (0, 0) to the final position (-3 m, 4 m).
Step 1: Identify the Initial and Final Positions
- Initial Position ri=(0,0)
- Final Position rf=(−3,4)
Step 2: Calculate the Displacement Vector
The displacement vector x can be calculated using the formula:
x=rf−ri
Substituting the values:
x=(−3,4)−(0,0)=(−3,4)
In vector notation, this can be expressed as:
x=−3^i+4^j
Step 3: Write the Force Vector
The force vector F is given as:
F=7^i−6^j
Step 4: Calculate the Work Done
The work done W by the force when moving through the displacement can be calculated using the dot product:
W=F⋅x
Substituting the vectors:
W=(7^i−6^j)⋅(−3^i+4^j)
Calculating the dot product:
W=(7⋅−3)+(−6⋅4)
W=−21−24
W=−45 Joules
Final Answer
The work done by the force is:
W=−45 Joules
- Initial Position ri=(0,0)
- Final Position rf=(−3,4)
The displacement vector x can be calculated using the formula:
x=rf−ri
Substituting the values:
x=(−3,4)−(0,0)=(−3,4)
In vector notation, this can be expressed as:
x=−3^i+4^j
The force vector F is given as:
F=7^i−6^j
The work done W by the force when moving through the displacement can be calculated using the dot product:
W=F⋅x
Substituting the vectors:
W=(7^i−6^j)⋅(−3^i+4^j)
Calculating the dot product:
W=(7⋅−3)+(−6⋅4)
W=−21−24
W=−45 Joules
The work done by the force is:
W=−45 Joules
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - D Matrix Matching Type Questions
10 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
One of the forces acting on the particle is conservative, then
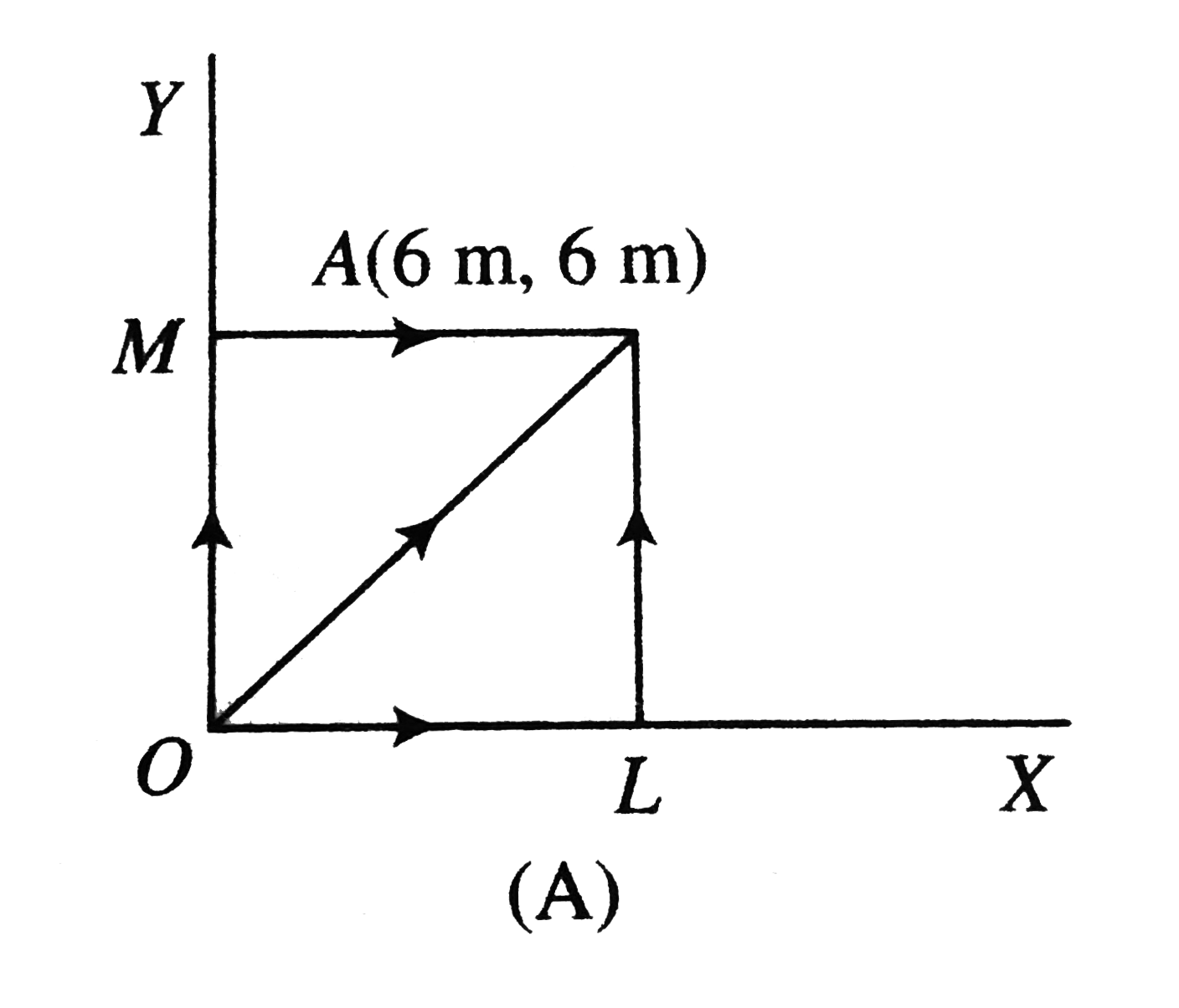
View SolutionForce acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force →F=(4ˆi+3ˆj)N acts on a particle of mass 2kg. The particle under the action of this force moves from the origin to a point A (4m,−8m). Initial speed of the particle, i.e., its speed at the origin is 2√6ms−1. Figure shows three paths for the motion of the particle from O to A.
If the potential energy at O is 16J, the potential energy at A will be
View Solution
Knowledge Check
A particle is acted upon by a force F which varies with position x is shown in figure .If the particle at x=0 kinetic energy of 25J then the kinetic energy of the particle at x=16m is
 A45 JB30 JC70 JD20 J
A45 JB30 JC70 JD20 JA force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
A563 JB560 JC5603 JD3560 J
A particle moves 5m in the +x direction while being acted upon by a constant force→F=(4N)ˆi+(2N)ˆj−(4N)ˆk . The work done on the particle by this force is
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionA particle of mass 2kg moves in the xy plane under the action of a constant force →F where →F=ˆi−ˆj. Initially the velocity of the particle is 2ˆj. The velocity of the particle at time t is
View SolutionDescribe the motion of a particle acted upon by the force:
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle of position vector (3ˆi+2ˆj+ˆk). Calculate the torque acting on the particle.
View SolutionA particle is moved from (0, 0) to (a, a) under a force a F=(3ˆi+4ˆj) from two paths. Path 1 is OP and path 2 is OPQ. Let W1 and W2 be the work done by this force in these two paths. Then,
View Solution
