A rectangular loop of sides a and b is placed in xy-placed. A uniform but time varying magnetic field of strength B=20tˆi+10t2ˆj+50ˆk is present in the region. The magnitude of induced emf in the loop at time is
20+20t
20
20t
zero
The correct Answer is:D
To solve the problem of finding the induced electromotive force (emf) in a rectangular loop placed in a time-varying magnetic field, we can follow these steps:
Step 1: Define the Area Vector
The rectangular loop lies in the xy-plane. Therefore, the area vector →A of the loop can be defined as:
→A=A^k=ab^k
where a and b are the lengths of the sides of the rectangle, and ^k indicates that the area vector is perpendicular to the plane of the loop.
Step 2: Define the Magnetic Field
The magnetic field →B is given as:
→B=20t^i+10t2^j+50^k
Step 3: Calculate the Magnetic Flux
The magnetic flux Φ through the loop is given by the dot product of the magnetic field →B and the area vector →A:
Φ=→B⋅→A=(20t^i+10t2^j+50^k)⋅(ab^k)
Calculating the dot product:
Φ=20t⋅0+10t2⋅0+50⋅ab=50ab
Step 4: Determine the Induced EMF
The induced emf E in the loop can be calculated using Faraday's law of electromagnetic induction, which states:
E=−dΦdt
Since the magnetic flux Φ is constant (it does not depend on time), the derivative of the flux with respect to time is:
dΦdt=0
Thus, the induced emf is:
E=−0=0
Conclusion
The magnitude of the induced emf in the loop at any time t is:
E=0
---
The rectangular loop lies in the xy-plane. Therefore, the area vector →A of the loop can be defined as:
→A=A^k=ab^k
where a and b are the lengths of the sides of the rectangle, and ^k indicates that the area vector is perpendicular to the plane of the loop.
The magnetic field →B is given as:
→B=20t^i+10t2^j+50^k
The magnetic flux Φ through the loop is given by the dot product of the magnetic field →B and the area vector →A:
Φ=→B⋅→A=(20t^i+10t2^j+50^k)⋅(ab^k)
Calculating the dot product:
Φ=20t⋅0+10t2⋅0+50⋅ab=50ab
The induced emf E in the loop can be calculated using Faraday's law of electromagnetic induction, which states:
E=−dΦdt
Since the magnetic flux Φ is constant (it does not depend on time), the derivative of the flux with respect to time is:
dΦdt=0
Thus, the induced emf is:
E=−0=0
The magnitude of the induced emf in the loop at any time t is:
E=0
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective
21 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A reacangular loop if size (2m×1m) is placed in x-y plane. A uniform but time varying magnetic field of strength T where t is the time elsapsed in second exists in sosace. The magnitude of induced emf (in V) at time t is
View SolutionA circular current carrying loop is placed in x-y plane as shown in figure. A uniform magnetic field B=B0ˆK is present in the region. Match the following.


View SolutionA circular loop of radius R carrying current I is kept in XZ plane. A uniform and constant magnetic field →B=(B0ˆi+2B0ˆj+3B0ˆk) exists in the region (B0− a positive constant). Then the magnitude of the torque acting on the loop will be
View SolutionIn Fig. there is a frame consisting of two square loops having resistors and inductors as shown. This frame is placed in a uniform but time-varying magnetic field in such a way that one of the loops is placed in crossed magentic field and the other is placed in dot magnetic field. Both magnetic fields are perpendicular to the planes of the loops.
If the magnetic field is given by B=(20+10t)Wbm−2 in both regions [l=20cm,b=10cm, and R=10Ω, L=10H),
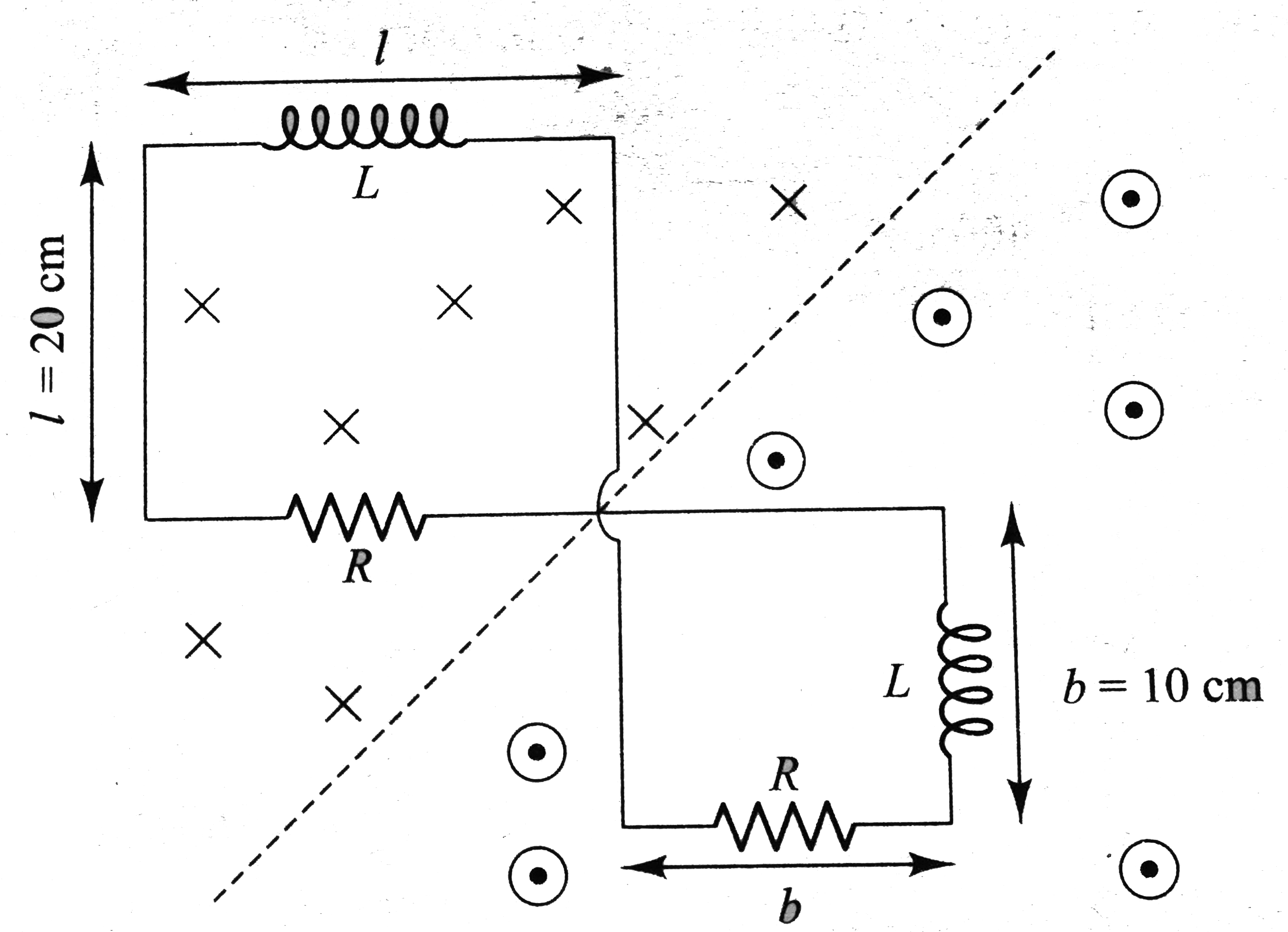
The direction in induced current in the bigger loop will be
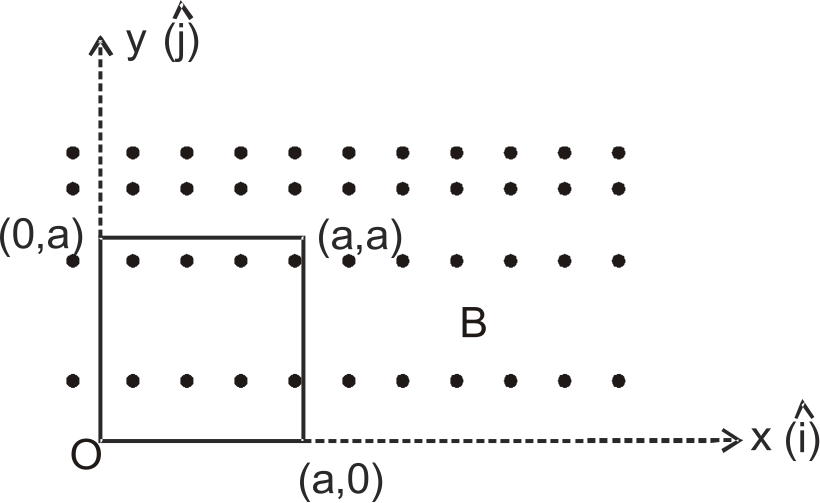
View SolutionA square loop of side 'a' is placed in x−y plane as shown in figure. In this region there is non-uniform time dependent magnetic field →B=(cy3t2)→k, [where t is time and c is constant] then magnitude of emf induced in loop is
View SolutionIn Fig. there is a frame consisting of two square loops having resistors and inductors as shown. This frame is placed in a uniform but time-varying magnetic field in such a way that one of the loops is placed in crossed magentic field and the other is placed in dot magnetic field. Both magnetic fields are perpendicular to the planes of the loops.
If the magnetic field is given by B=(20+10t)Wbm−2 in both regions [l=20cm,b=10cm, and R=10Ω, L=10H),
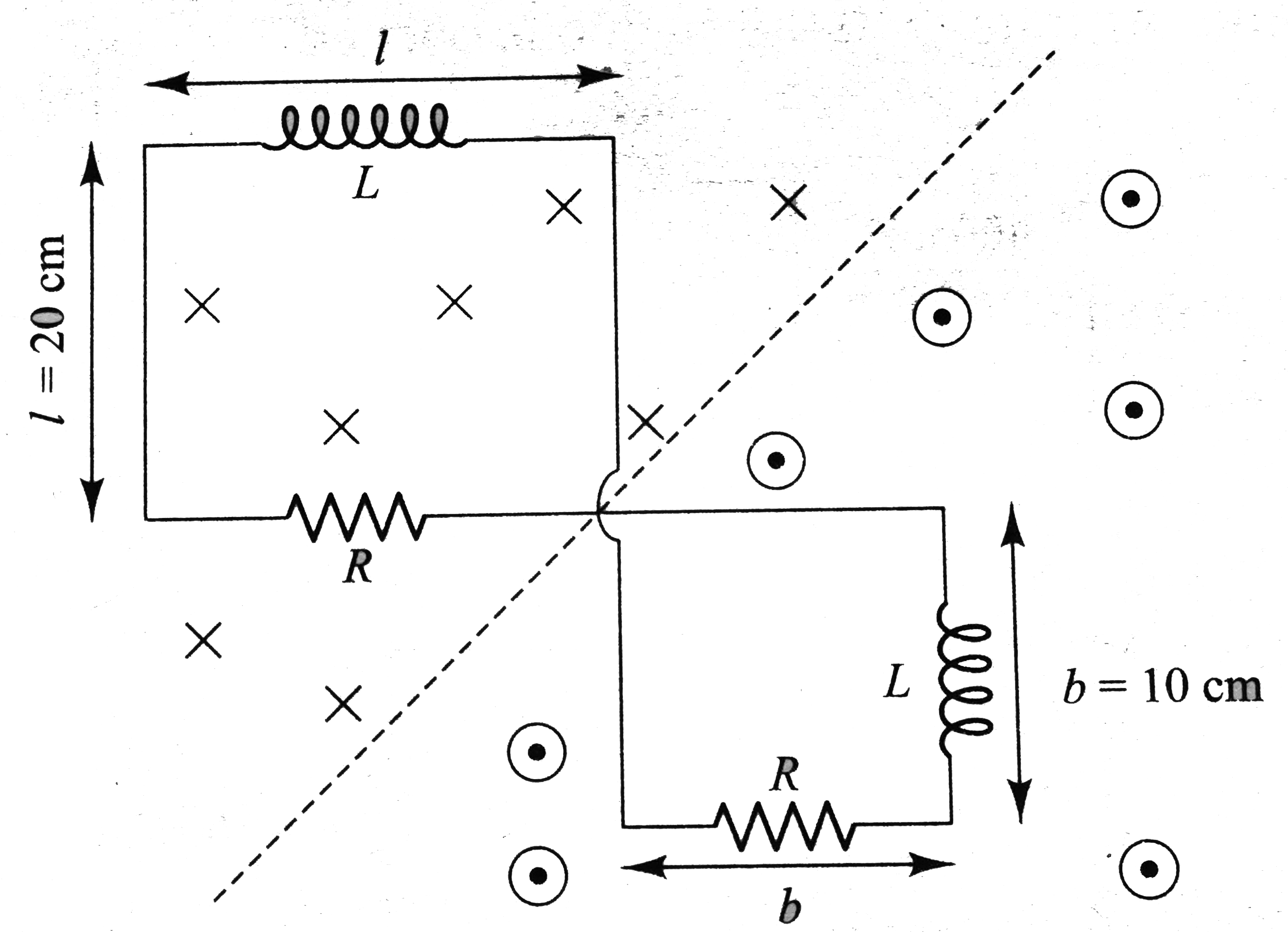
The current in the frame as a funtion of time will be
View SolutionIn Fig. there is a frame consisting of two square loops having resistors and inductors as shown. This frame is placed in a uniform but time-varying magnetic field in such a way that one of the loops is placed in crossed magentic field and the other is placed in dot magnetic field. Both magnetic fields are perpendicular to the planes of the loops.
If the magnetic field is given by B=(20+10t)Wbm−2 in both regions [l=20cm,b=10cm, and R=10Ω, L=10H),
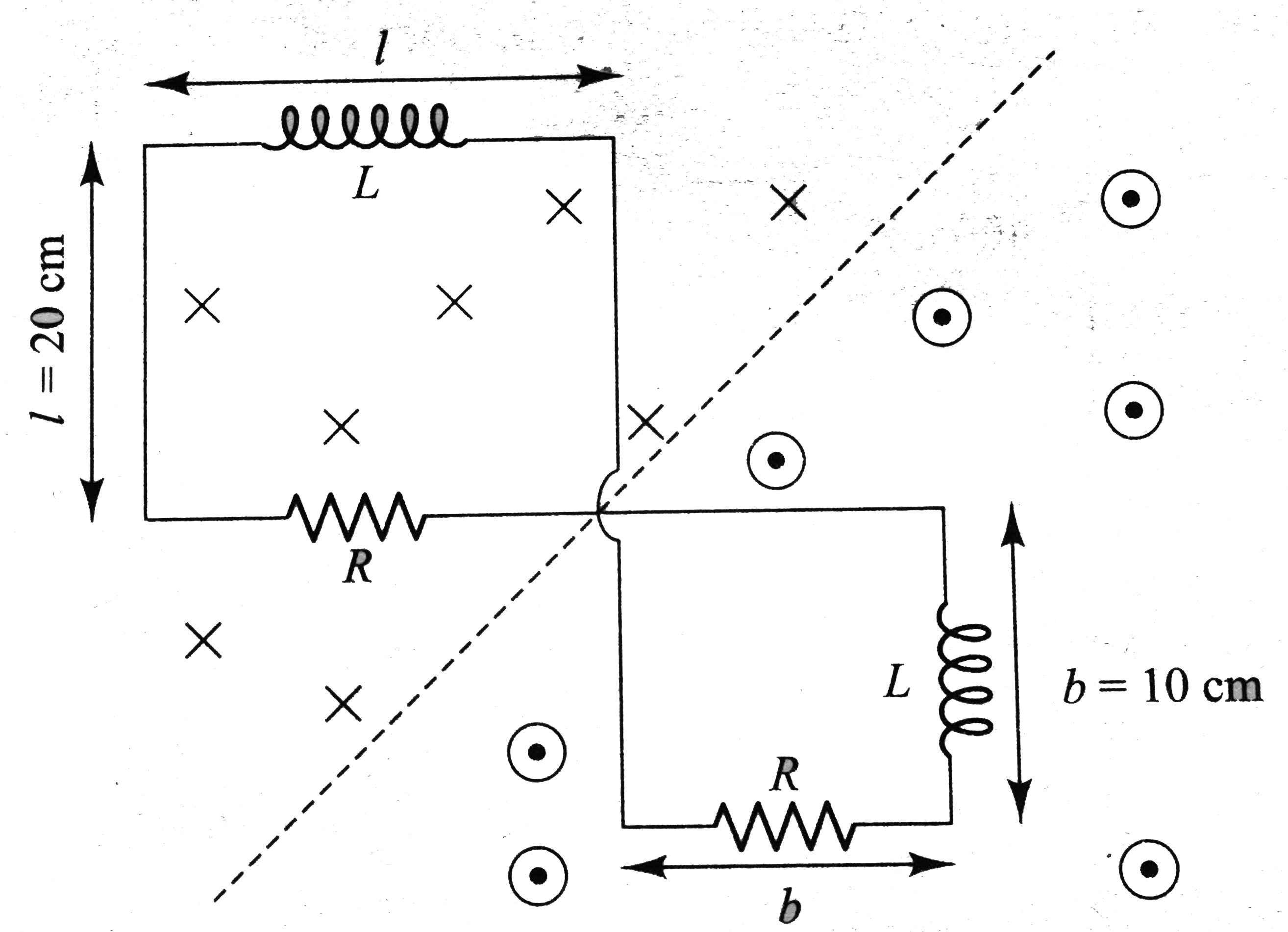
The induced emf in the frame only due to the vartation of magnetic field will be
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnituded 0.20 T exists parallel ot the longer side of the loop (a) What is the force acting on the loop? (b) what is the torque acting on the loop?
View Solution
