A reacangular loop if size (2m×1m) is placed in x-y plane. A uniform but time varying magnetic field of strength T where t is the time elsapsed in second exists in sosace. The magnitude of induced emf (in V) at time t is
20=20i
20
20i
zero
The correct Answer is:D
To solve the problem of finding the induced EMF in a rectangular loop placed in a time-varying magnetic field, we can follow these steps:
1. Identify the dimensions of the loop:
The rectangular loop has dimensions of 2 meters by 1 meter. Therefore, the area A of the loop can be calculated as:
A=length×width=2m×1m=2m2
Hint: Remember that the area of a rectangle is simply the product of its length and width.
2. Determine the magnetic field:
The magnetic field B is given as:
B=2T^i+10T2^j+50T^k
Here, the magnetic field has components in the x, y, and z directions.
Hint: Break down the magnetic field into its components to understand how it varies with time.
3. Calculate the magnetic flux (Φ):
The magnetic flux through the loop is given by the dot product of the magnetic field and the area vector. Since the loop is in the x-y plane, the area vector A points in the z-direction:
A=A^k=2^k
The magnetic flux Φ is calculated as:
Φ=B⋅A=(2^i+10^j+50^k)⋅(2^k)=50×2=100Wb
The contributions from the ^i and ^j components are zero because they are perpendicular to ^k.
Hint: Remember that the dot product only contributes when the vectors are in the same direction.
4. Determine the induced EMF (E):
The induced EMF is given by Faraday's law of electromagnetic induction:
E=−dΦdt
Since the magnetic flux Φ is constant (as it does not depend on time), the derivative dΦdt is zero:
E=−0=0V
Hint: If the magnetic flux is constant, the induced EMF will be zero.
5. Conclusion:
The magnitude of the induced EMF at time t is:
E=0V
Final Answer:
The magnitude of induced EMF at time t is 0V.
The rectangular loop has dimensions of 2 meters by 1 meter. Therefore, the area A of the loop can be calculated as:
A=length×width=2m×1m=2m2
The magnetic field B is given as:
B=2T^i+10T2^j+50T^k
Here, the magnetic field has components in the x, y, and z directions.
The magnetic flux through the loop is given by the dot product of the magnetic field and the area vector. Since the loop is in the x-y plane, the area vector A points in the z-direction:
A=A^k=2^k
The magnetic flux Φ is calculated as:
Φ=B⋅A=(2^i+10^j+50^k)⋅(2^k)=50×2=100Wb
The contributions from the ^i and ^j components are zero because they are perpendicular to ^k.
The induced EMF is given by Faraday's law of electromagnetic induction:
E=−dΦdt
Since the magnetic flux Φ is constant (as it does not depend on time), the derivative dΦdt is zero:
E=−0=0V
The magnitude of the induced EMF at time t is:
E=0V
The magnitude of induced EMF at time t is 0V.
Topper's Solved these Questions
Similar Questions
A rectangular loop of sides a and b is placed in xy-placed. A uniform but time varying magnetic field of strength B=20tˆi+10t2ˆj+50ˆk is present in the region. The magnitude of induced emf in the loop at time is
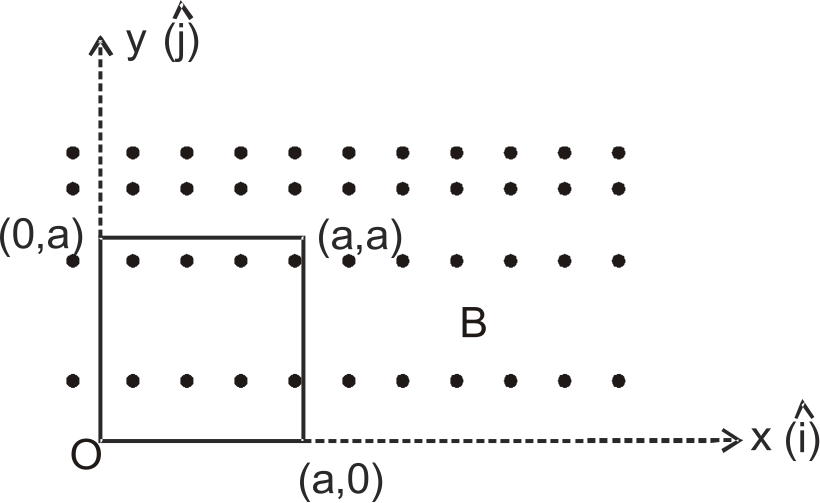
View SolutionA square loop of side 'a' is placed in x−y plane as shown in figure. In this region there is non-uniform time dependent magnetic field →B=(cy3t2)→k, [where t is time and c is constant] then magnitude of emf induced in loop is
View SolutionMagnetic flux (in Wb) linked with a closed loop varies with time (in S) as Φ =2t^2+1. The magnitude of induced emf at t=1 s is
View SolutionMagnetic flux (in Wb) linked with a closed loop varies with time (in S) as Φ =2t^2+1. The magnitude of induced emf at t=1 s is
View SolutionIn Fig. there is a frame consisting of two square loops having resistors and inductors as shown. This frame is placed in a uniform but time-varying magnetic field in such a way that one of the loops is placed in crossed magentic field and the other is placed in dot magnetic field. Both magnetic fields are perpendicular to the planes of the loops.
If the magnetic field is given by B=(20+10t)Wbm−2 in both regions [l=20cm,b=10cm, and R=10Ω, L=10H),
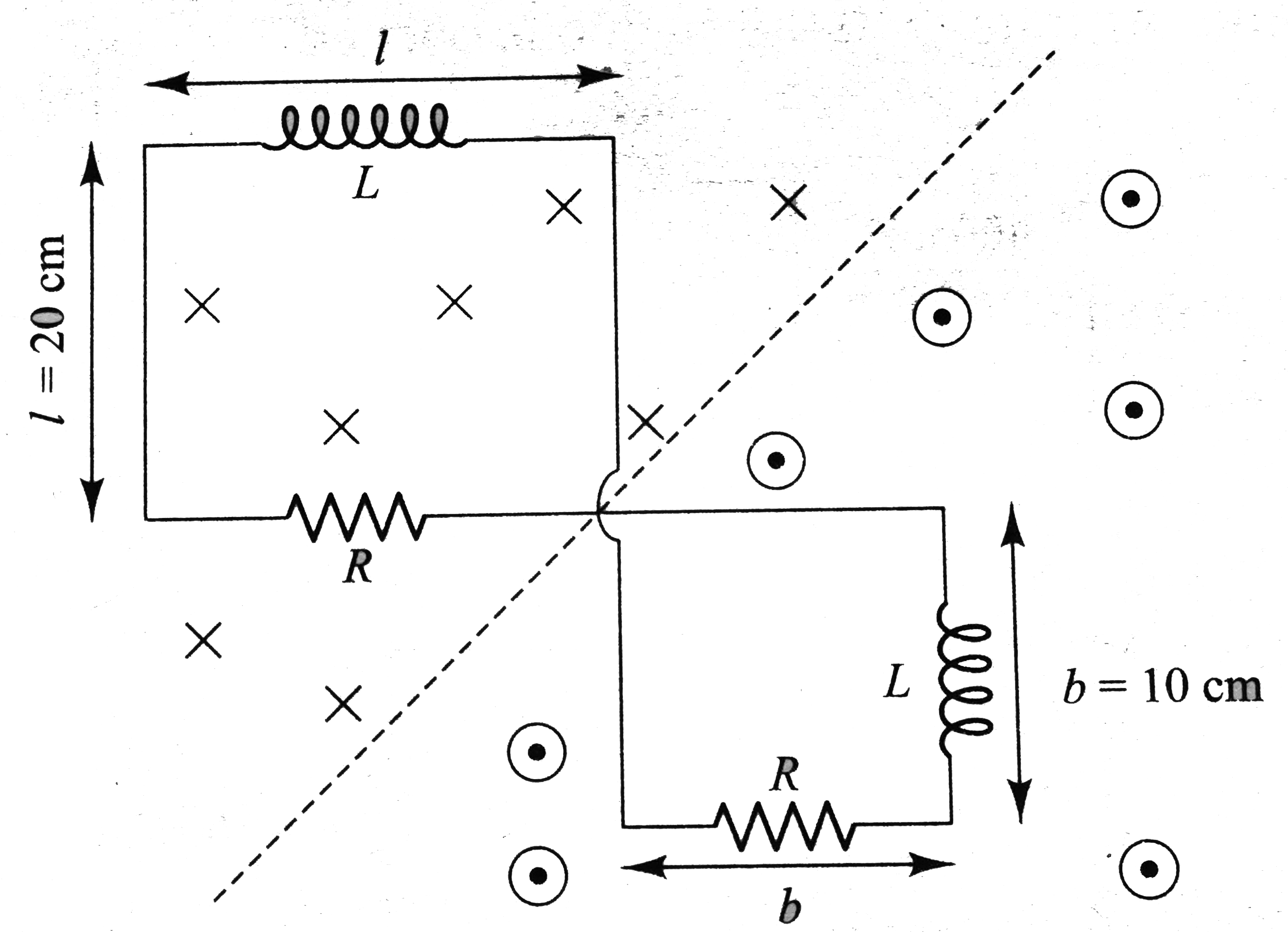
The current in the frame as a funtion of time will be
View SolutionIn Fig. there is a frame consisting of two square loops having resistors and inductors as shown. This frame is placed in a uniform but time-varying magnetic field in such a way that one of the loops is placed in crossed magentic field and the other is placed in dot magnetic field. Both magnetic fields are perpendicular to the planes of the loops.
If the magnetic field is given by B=(20+10t)Wbm−2 in both regions [l=20cm,b=10cm, and R=10Ω, L=10H),
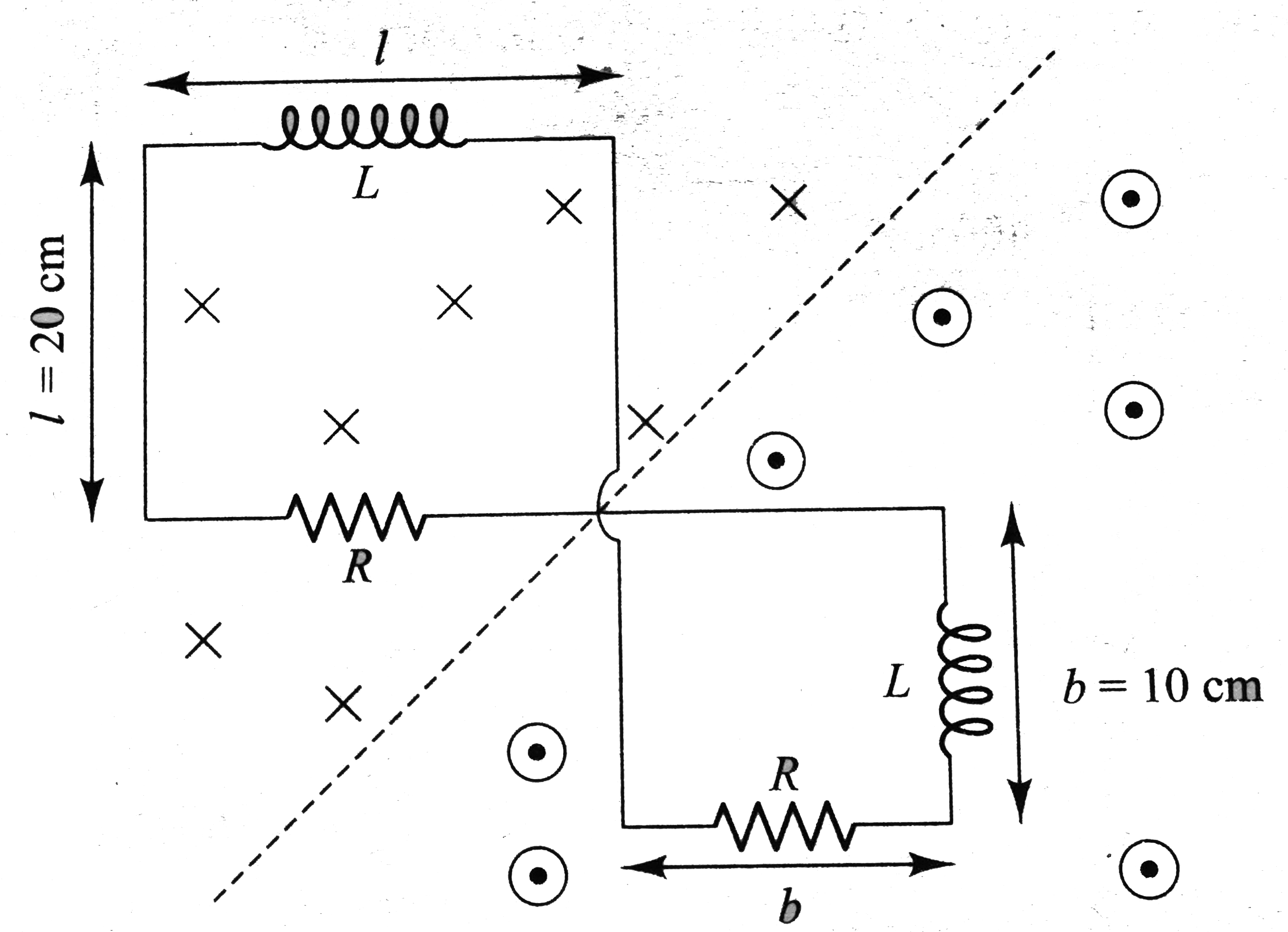
The direction in induced current in the bigger loop will be
View SolutionA circular loop of radius 1m is placed in a varying magnetic field given as B=6t Tesla, where t is time in sec.
(a)Find the emf induced in the coil if the plane of the coil is perpendicular to the magnetic field.
(b) Find the electric field in the tangential directin, induced due to the changing magnetic field.
(c)Find the current in the loop if its resistance is 1Ω/m.
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
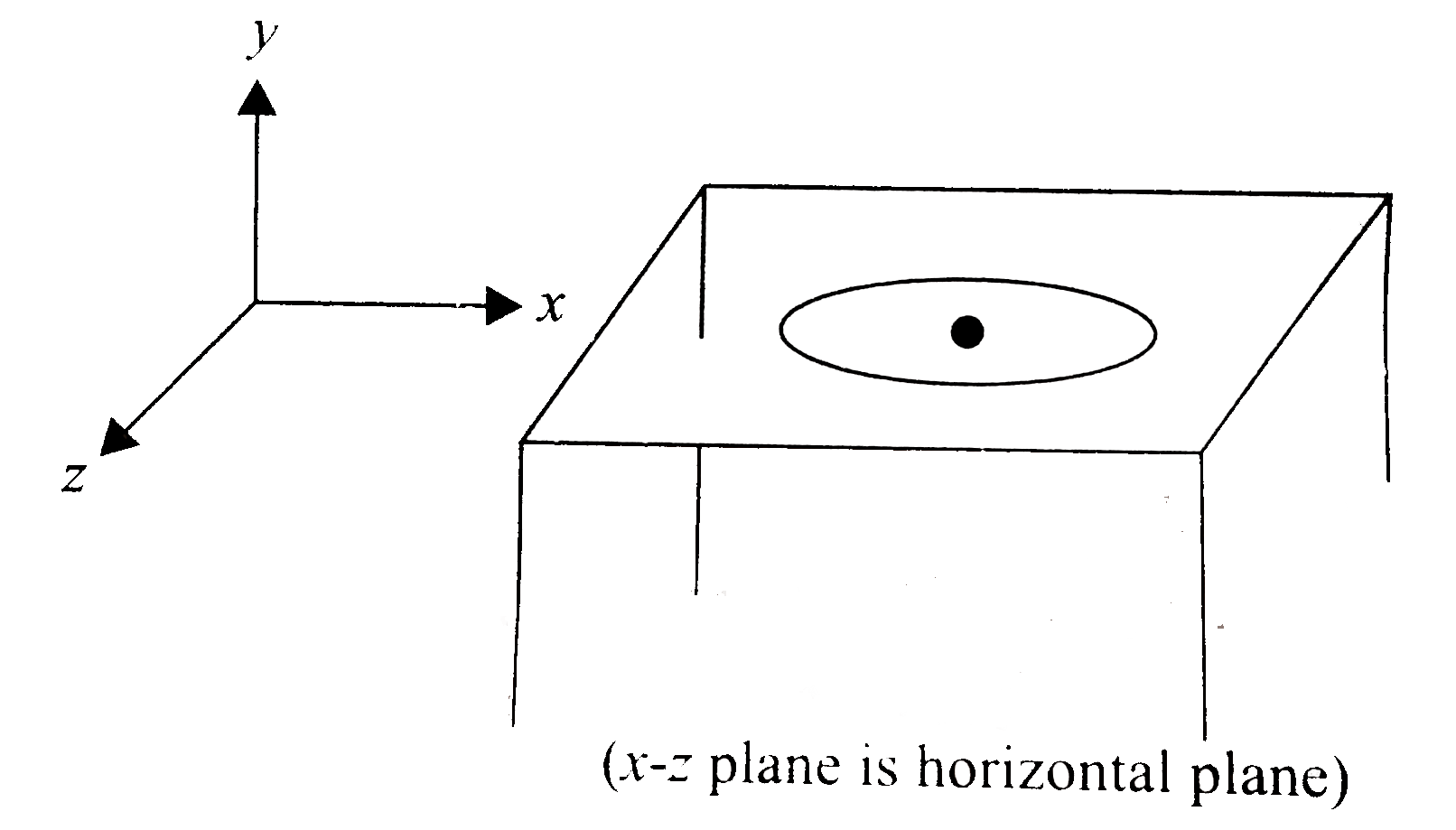
Net Induced EMF (in Volt) on conducting ring as function of time is
View SolutionThe entire network shown here, has uniform wire having resistance per unit length as 1Ω/m. It is placed in a uniform but time varying magnetic field →B(directed into the plane). If the strength of the magnetic field is increasing at 1T/s, the ratio I1/I2 equals

View SolutionA conducting circular loop of radius a and resistance R is kept on a horizontal plane. A vertical time varying magnetic field B=2t is switched on at time t=0. Then
View Solution
