A rectangular tank of mass and charge Q is placed over a smooth horizontal floor. A horizontal electric field E exist in the region. Rain drops are falling vertically in the tank at the constant rate of n drops per second. Mass of each drop is m. Find velocity of tank as function of time.
To find the velocity of the tank as a function of time, we will follow a systematic approach.
1. Understanding the Problem:
- We have a rectangular tank of mass m0 and charge Q.
- The tank is placed on a smooth horizontal floor.
- A horizontal electric field E is present.
- Rain drops are falling vertically into the tank at a constant rate of n drops per second, with each drop having a mass m.
2. Determine the Mass of Rainwater in the Tank:
- In time t, the total number of rain drops that have fallen into the tank is n⋅t.
- The total mass of the rainwater in the tank is given by:
mrain=n⋅t⋅m=mnt
3. Total Mass of the System:
- The total mass of the tank plus the rainwater is:
mtotal=m0+mnt
4. Applying Newton's Second Law:
- The net force acting on the tank is the difference between the electric force and the thrust force due to the falling rain.
- The electric force is given by:
Felectric=Q⋅E
- The thrust force (momentum change due to rain) is:
Fthrust=mnv
- Therefore, the net force can be expressed as:
Fnet=Felectric−Fthrust=QE−mnv
5. Setting Up the Equation of Motion:
- According to Newton's second law:
Fnet=mtotal⋅a=(m0+mnt)⋅dvdt
- Thus, we have:
(m0+mnt)dvdt=QE−mnv
6. Rearranging the Equation:
- Rearranging gives us:
dvdt=QE−mnvm0+mnt
7. Separating Variables:
- We can separate the variables to integrate:
dvQE−mnv=dtm0+mnt
8. Integrating Both Sides:
- Integrate the left side with respect to v and the right side with respect to t:
∫1QE−mnvdv=∫1m0+mntdt
- The left side integrates to:
−1mnln|QE−mnv|
- The right side integrates to:
1mnln|m0+mnt|
9. Combining Results:
- Combining the results from both integrals gives:
−ln|QE−mnv|=ln|m0+mnt|+C
- Exponentiating both sides leads to:
Q E - m n v = k (m_0 + m n t) \quad \text{(where k is a constant)}
10. Solving for Velocity:
- Rearranging gives:
v=QEmn−kmn(m0+mnt)
- To find k, we can use the initial condition v(0)=0:
0=QEmn−km0mn⟹k=QEm0
- Substituting k back gives the final expression for velocity:
v(t)=QEmn(1−m0m0+mnt)
Final Expression:
v(t)=QEmn(1−m0m0+mnt)
- We have a rectangular tank of mass m0 and charge Q.
- The tank is placed on a smooth horizontal floor.
- A horizontal electric field E is present.
- Rain drops are falling vertically into the tank at a constant rate of n drops per second, with each drop having a mass m.
- In time t, the total number of rain drops that have fallen into the tank is n⋅t.
- The total mass of the rainwater in the tank is given by:
mrain=n⋅t⋅m=mnt
- The total mass of the tank plus the rainwater is:
mtotal=m0+mnt
- The net force acting on the tank is the difference between the electric force and the thrust force due to the falling rain.
- The electric force is given by:
Felectric=Q⋅E
- The thrust force (momentum change due to rain) is:
Fthrust=mnv
- Therefore, the net force can be expressed as:
Fnet=Felectric−Fthrust=QE−mnv
- According to Newton's second law:
Fnet=mtotal⋅a=(m0+mnt)⋅dvdt
- Thus, we have:
(m0+mnt)dvdt=QE−mnv
- Rearranging gives us:
dvdt=QE−mnvm0+mnt
- We can separate the variables to integrate:
dvQE−mnv=dtm0+mnt
- Integrate the left side with respect to v and the right side with respect to t:
∫1QE−mnvdv=∫1m0+mntdt
- The left side integrates to:
−1mnln|QE−mnv|
- The right side integrates to:
1mnln|m0+mnt|
- Combining the results from both integrals gives:
−ln|QE−mnv|=ln|m0+mnt|+C
- Exponentiating both sides leads to:
Q E - m n v = k (m_0 + m n t) \quad \text{(where k is a constant)}
- Rearranging gives:
v=QEmn−kmn(m0+mnt)
- To find k, we can use the initial condition v(0)=0:
0=QEmn−km0mn⟹k=QEm0
- Substituting k back gives the final expression for velocity:
v(t)=QEmn(1−m0m0+mnt)
v(t)=QEmn(1−m0m0+mnt)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
A rectangular tank of mass m0 and charge Q over it is placed over a smooth horizontal floor. A horizontal electric field E exist in the region. Rain drops are falling vertically in the tank at the constant rate of n drops per second, Mass of each drop is m. Find velocity of tank as function of time.
View SolutionA ball of mass m having a charge q is released from rest in a region where a horizontal electric field E exists.
(a) Find the resultant force acting on the ball.
(b) Find the trajectory followed by the ball.View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionA particle of mass m and charge −q is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity
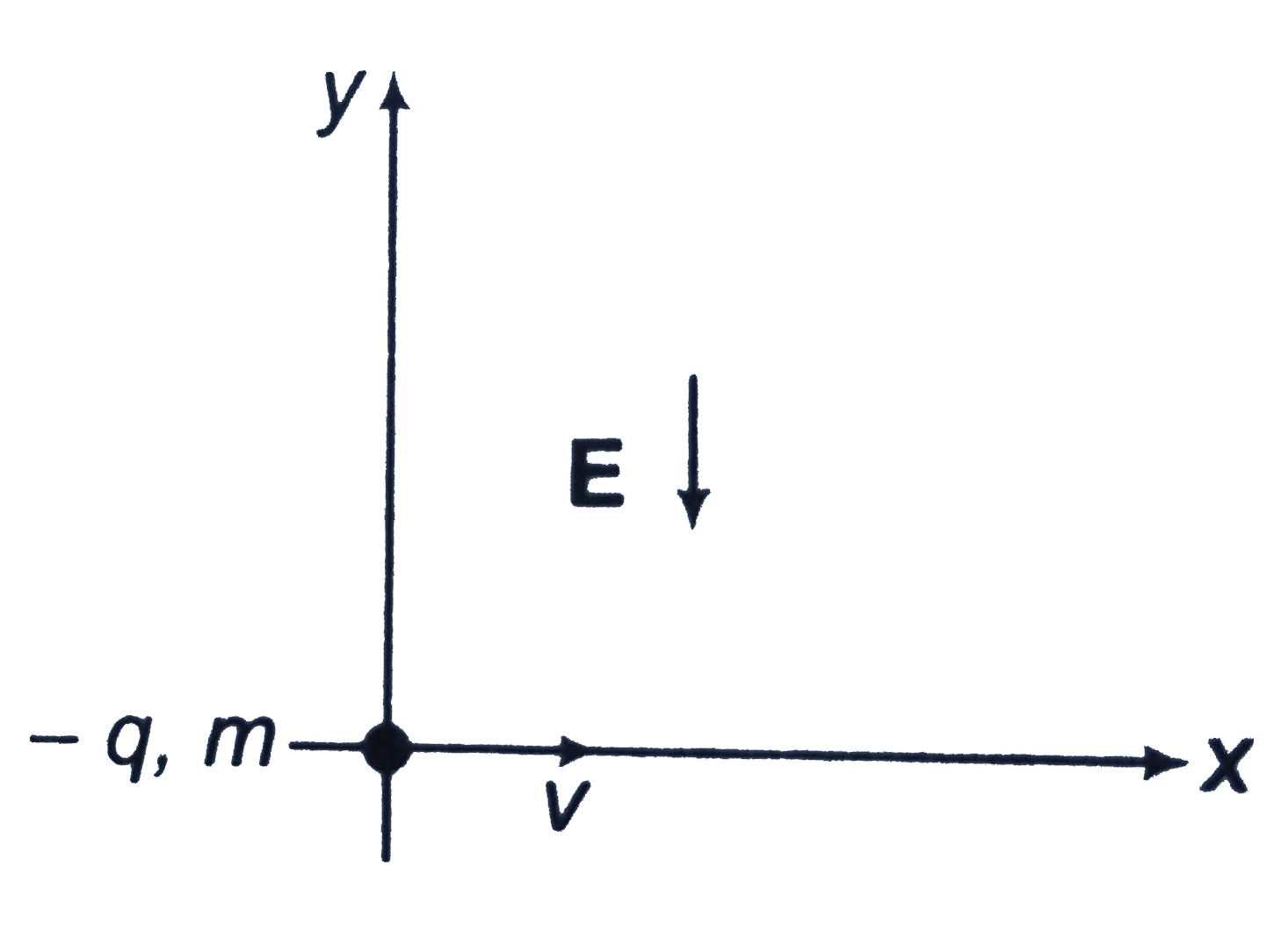 View Solution
View SolutionA particle of mass m and charge −q is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity
 View Solution
View SolutionA conducting rod of mass m and length l is placed over a smooth horizontal surface. A uniform magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed through the rod and it acquires an initial velocity v on the surface, then q is equal to
View SolutionA block of mass m having a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k as shown in figure(29.E1) . A horizontal electric field E parallel to the spring is switched on. Find the amplitude of the resulting SHM of the block.
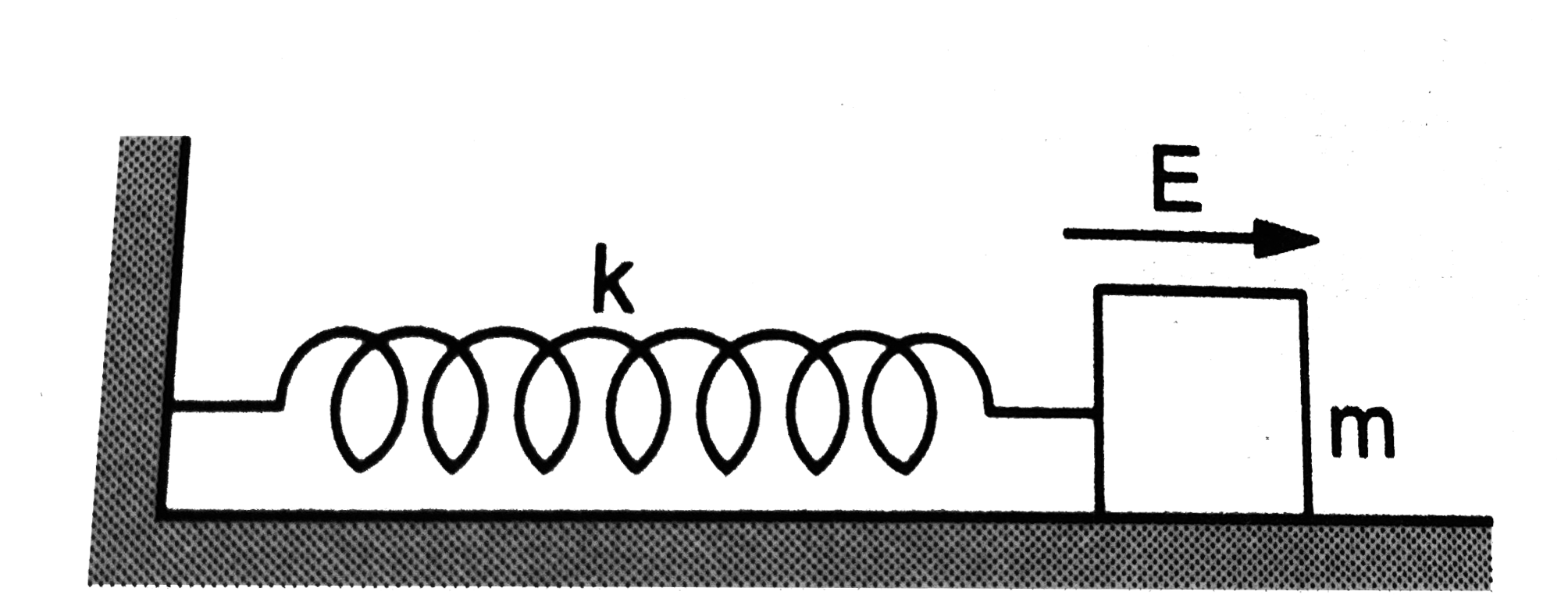 View Solution
View SolutionA small particle of mass m and charge Q is dropped in uniform horizontal magnetic field B. The maximum vertical displacement of particle is given by h=nm2g2Q2B2 . Find the value n.
View SolutionA wire is wrapped N times over a solid sphere of mass m which is place on a smooth horizontal surface. A horizontal magnetic field of induction →B is present. Find the (a) torque (b) angular acceleration experienced by the sphere. Assume that the mass of the wire is negligible compared to the mass of the sphere.
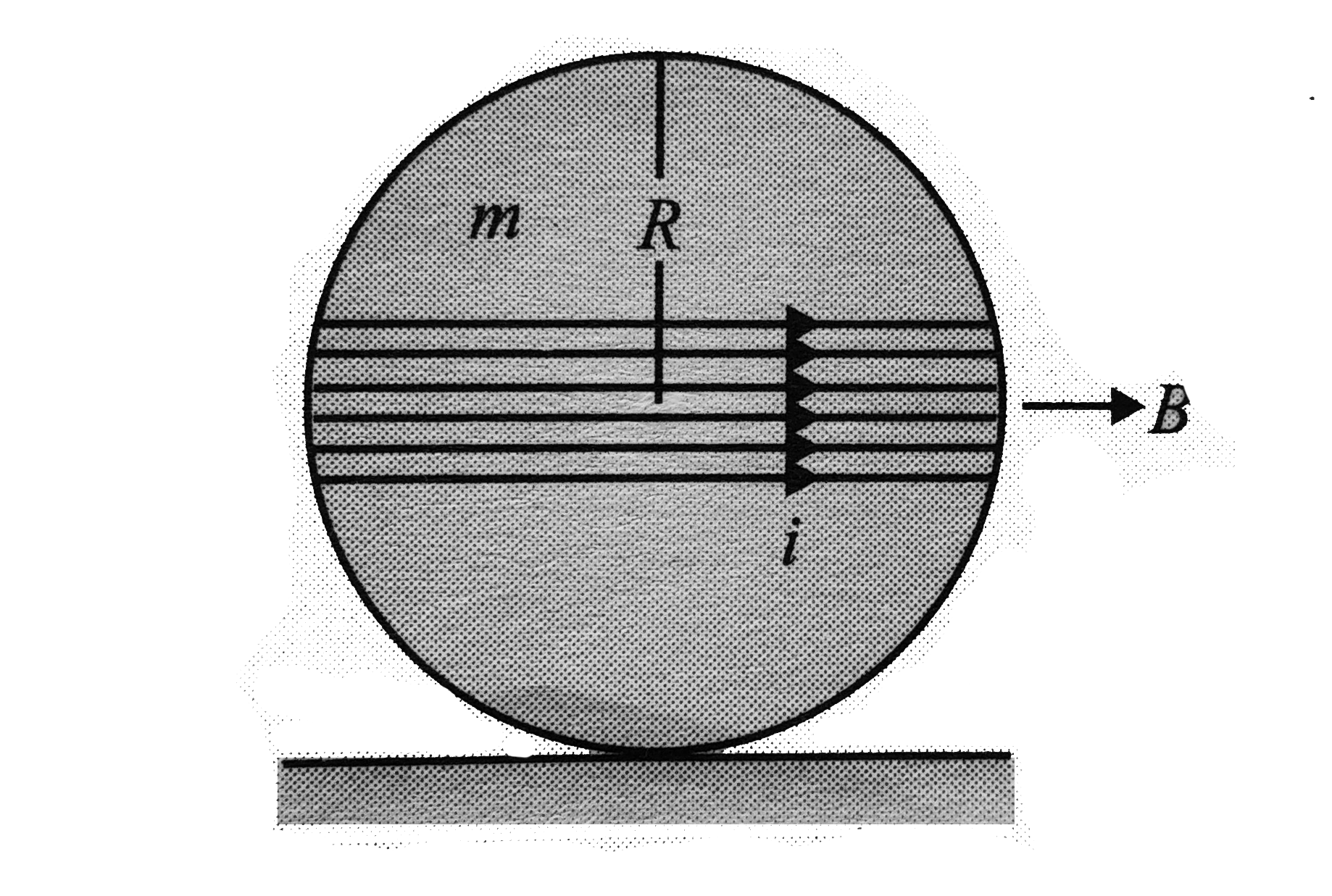 View Solution
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View Solution

