A wire of linear charge density λ passes through a cuboid of length l, breadth b and height h(l>b>h) in such a manner that the flux through the cuboid is maximum. The position of the wire is now changed, so that the flux through the cuboid is minimum. The raito of maximum flux to minimum flux will be
√l2+b2+h2h
√l2+b2h
h√l2+b2
l√l2+b2+h2
The correct Answer is:A
To solve the problem, we need to find the ratio of the maximum electric flux to the minimum electric flux through a cuboid when a wire with linear charge density λ passes through it.
1. Understanding Electric Flux:
The electric flux Φ through a closed surface is given by Gauss's law:
Φ=Qencϵ0
where Qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
2. Maximum Flux Condition:
To maximize the flux through the cuboid, the wire should pass through the body diagonal of the cuboid. The body diagonal d of a cuboid with dimensions l, b, and h is given by:
d=√l2+b2+h2
The total charge Qmax enclosed when the wire passes through the body diagonal is:
Qmax=λ⋅d=λ⋅√l2+b2+h2
3. Minimum Flux Condition:
To minimize the flux through the cuboid, the wire should pass through the cuboid such that it covers only the smallest dimension, which is h (since l>b>h). Thus, the total charge Qmin enclosed in this case is:
Qmin=λ⋅h
4. Calculating the Fluxes:
Using Gauss's law, the maximum and minimum fluxes can be expressed as:
Φmax=Qmaxϵ0=λ⋅√l2+b2+h2ϵ0
Φmin=Qminϵ0=λ⋅hϵ0
5. Finding the Ratio of Maximum to Minimum Flux:
The ratio of maximum flux to minimum flux is:
ΦmaxΦmin=λ⋅√l2+b2+h2ϵ0λ⋅hϵ0=√l2+b2+h2h
6. Final Result:
Thus, the ratio of maximum flux to minimum flux is:
ΦmaxΦmin=√l2+b2+h2h
The electric flux Φ through a closed surface is given by Gauss's law:
Φ=Qencϵ0
where Qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
To maximize the flux through the cuboid, the wire should pass through the body diagonal of the cuboid. The body diagonal d of a cuboid with dimensions l, b, and h is given by:
d=√l2+b2+h2
The total charge Qmax enclosed when the wire passes through the body diagonal is:
Qmax=λ⋅d=λ⋅√l2+b2+h2
To minimize the flux through the cuboid, the wire should pass through the cuboid such that it covers only the smallest dimension, which is h (since l>b>h). Thus, the total charge Qmin enclosed in this case is:
Qmin=λ⋅h
Using Gauss's law, the maximum and minimum fluxes can be expressed as:
Φmax=Qmaxϵ0=λ⋅√l2+b2+h2ϵ0
Φmin=Qminϵ0=λ⋅hϵ0
The ratio of maximum flux to minimum flux is:
ΦmaxΦmin=λ⋅√l2+b2+h2ϵ0λ⋅hϵ0=√l2+b2+h2h
Thus, the ratio of maximum flux to minimum flux is:
ΦmaxΦmin=√l2+b2+h2h
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A: When the magnetic flux through a loop is maximum, induced emf is maximum.
R: When the magnetic flux through a loop is minimum, induced emf is minimum.
View SolutionAn infinite wire having charge density λ passes through one of the edges of a cube having edge length l.
a. Find the total flux passing through the cube.
b. Find the flux passing through the surfaces in contact with the wire.
c. Find the flux passing through the surfaces not in contact with the wire.

View SolutionA long string with a charge of λ per unit length passes through an imaginary cube of edge a. The maximum flux of the electric field through the cube will be
View SolutionTwelve infinite long wire of uniform linear charge density (λ) are passing along the twelve edges of a cube. Find electric flux through any face of cube. ,
View SolutionA vessel of length l, breadth b and height h is filled completely with a liquid of density d (see figure) Calculate the thrust on each surface of the cube.
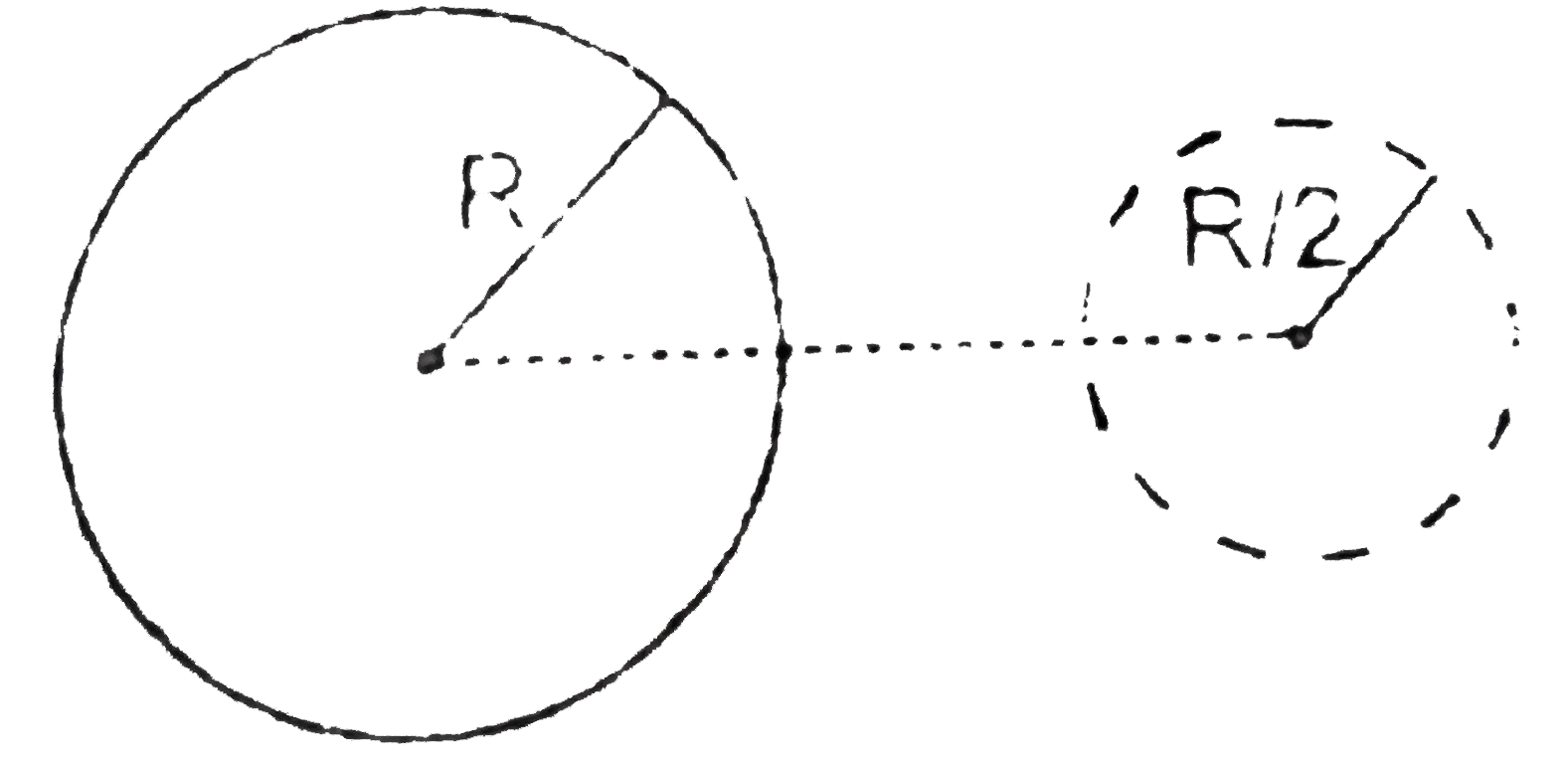
View SolutionA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
View Solution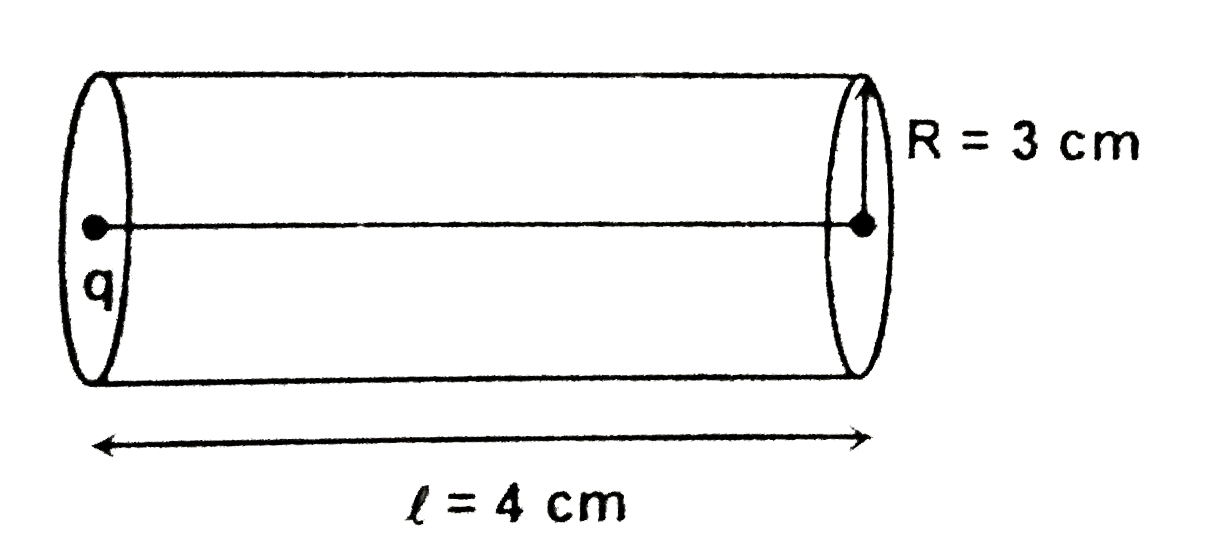
A point charge 'q' is placed at the centre of left circular end of a cylinder of length l=4cm and radius R=3 cm shown. Then the electric flux through the curved surface of the cylinder is
View SolutionA thin straight infinitely long conducting wire having charge density λ enclosed bya cylindrical surface of radius rand length lr, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
View SolutionThe length of each side of a cubical closed surface is L metre. If charge 48C is situated at one of the corners of the cube, Find the flux passing through the cube. (In Volt-metre)
View SolutionA thin wire of linear charge density λ is bent in the form of a triangle ABC and an imaginary cube of side .a. is taken with vertex A at the centre of the top face and vertices B,C at the opposite edge centres of the bottom face. The total electric flux linked with the cube is
View Solution
