Calculate the capacity of unknown capacitance is connected acrosss a battery of V volts. The charge stored in it is 360μC. When potential across the capacitor is reduced by 120V, the charge stored in it becomes 120μC.
Calculate (i) the potential V and unknown capacitance C. (ii) What will be the charge stored in the capacitor. If the voltage applied had increased by 120 V
To solve the problem, we will follow these steps:
Step 1: Establish the relationship between charge, capacitance, and voltage
The charge Q stored in a capacitor is given by the formula:
Q=C⋅V
where C is the capacitance and V is the voltage across the capacitor.
Step 2: Set up the first equation
From the problem, we know that when the capacitor is connected to a battery of V volts, the charge stored is 360μC. Therefore, we can write:
360×10−6=C⋅V(Equation 1)
Step 3: Set up the second equation
When the potential across the capacitor is reduced by 120V, the new charge stored is 120μC. The new voltage across the capacitor is V−120. Thus, we can write:
120×10−6=C⋅(V−120)(Equation 2)
Step 4: Solve the two equations
Now we have two equations:
1. C=360×10−6V
2. C=120×10−6V−120
Setting these two expressions for C equal to each other:
360×10−6V=120×10−6V−120
Step 5: Cross-multiply and simplify
Cross-multiplying gives us:
360×10−6⋅(V−120)=120×10−6⋅V
Dividing both sides by 10−6 simplifies to:
360(V−120)=120V
Expanding the left side:
360V−43200=120V
Rearranging gives:
360V−120V=43200
240V=43200
Dividing both sides by 240:
V=43200240=180V
Step 6: Calculate the unknown capacitance C
Now substituting V=180V back into Equation 1:
C=360×10−6180=2×10−6F=2μF
Step 7: Calculate the charge if the voltage is increased by 120V
If the voltage is increased by 120V, the new voltage V′=V+120=180+120=300V. The charge stored in the capacitor can be calculated as:
Q′=C⋅V′=2×10−6⋅300=600×10−6C=600μC
Final Answers:
(i) The potential V=180V and the unknown capacitance C=2μF.
(ii) The charge stored in the capacitor when the voltage is increased by 120V is 600μC.
---
The charge Q stored in a capacitor is given by the formula:
Q=C⋅V
where C is the capacitance and V is the voltage across the capacitor.
From the problem, we know that when the capacitor is connected to a battery of V volts, the charge stored is 360μC. Therefore, we can write:
360×10−6=C⋅V(Equation 1)
When the potential across the capacitor is reduced by 120V, the new charge stored is 120μC. The new voltage across the capacitor is V−120. Thus, we can write:
120×10−6=C⋅(V−120)(Equation 2)
Now we have two equations:
1. C=360×10−6V
2. C=120×10−6V−120
360×10−6V=120×10−6V−120
Cross-multiplying gives us:
360×10−6⋅(V−120)=120×10−6⋅V
Dividing both sides by 10−6 simplifies to:
360(V−120)=120V
Expanding the left side:
360V−43200=120V
Rearranging gives:
360V−120V=43200
240V=43200
Dividing both sides by 240:
V=43200240=180V
Now substituting V=180V back into Equation 1:
C=360×10−6180=2×10−6F=2μF
If the voltage is increased by 120V, the new voltage V′=V+120=180+120=300V. The charge stored in the capacitor can be calculated as:
Q′=C⋅V′=2×10−6⋅300=600×10−6C=600μC
(i) The potential V=180V and the unknown capacitance C=2μF.
(ii) The charge stored in the capacitor when the voltage is increased by 120V is 600μC.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]
Explore 11 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)
Explore 5 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SECTION-B
Explore 52 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
A capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 300 μC. When potential across the capacitor is reduced by 100 V, the charge stored in it becomes 100 μC. Calculate the potential V and the unknown capacitance. What will be the charge stored in the capacitor if the voltage applied had increased by 100V?
View SolutionIn the given circuit, with steady current, calculate the potential difference across the capacitor and the charge stored in it.
View Solution
Knowledge Check
A capacitor of capacitance 700 pF is charged by 100 V battery. The electrostatic energy stored by the capacitor is
A2.5×10−8JB3.5×10−6JC2.5×10−4JD3.5×10−4J
A capacitor of capacitance 6 μF is connected with an emf sourface 3 V. Electrostaci energy stored in the capacitor is
View SolutionSeveral capacitors are connected as shown in. If the charge on the 5μF capacitor is 120μC, the potential between points A and D is
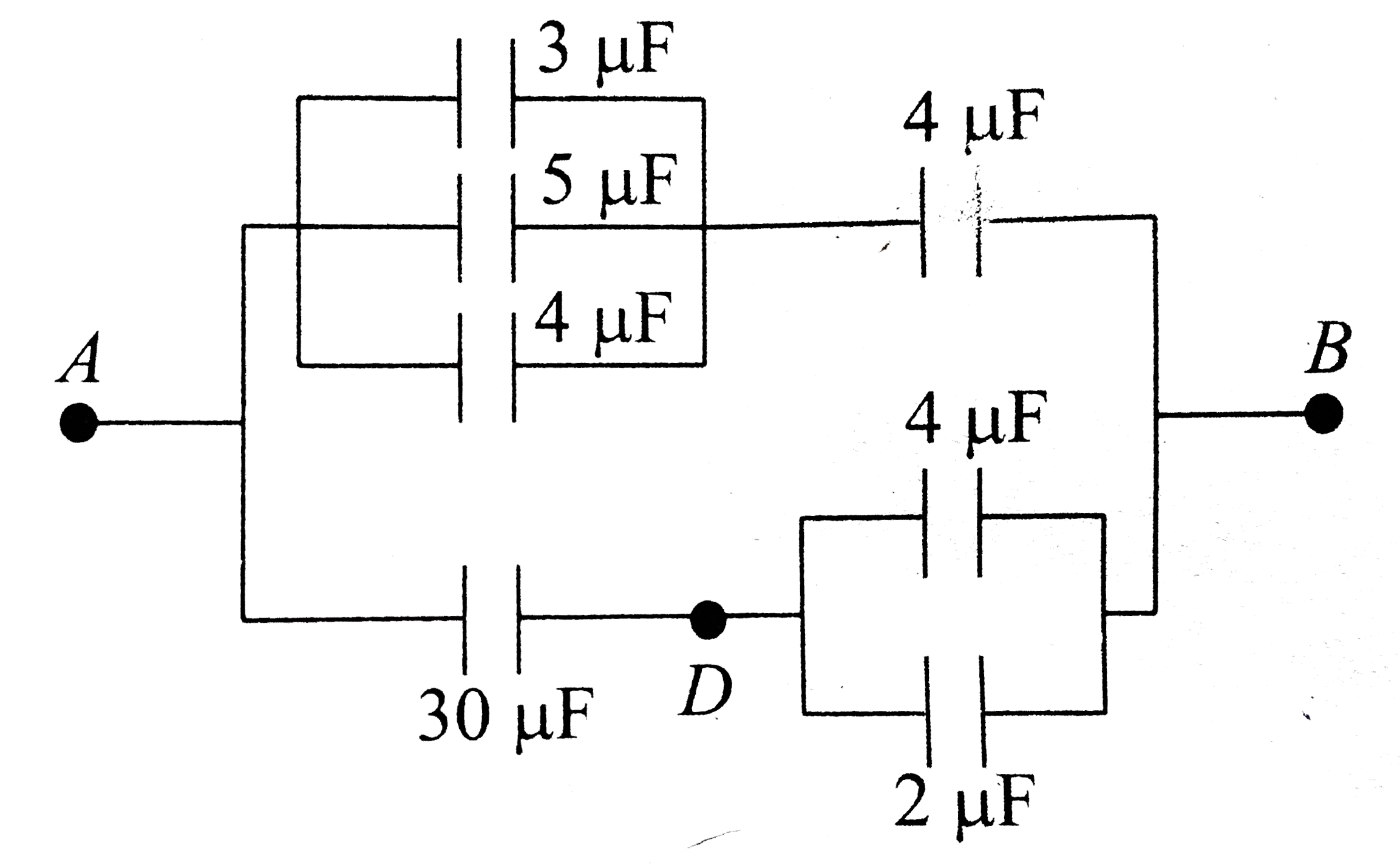 .
.
View SolutionHow many 1μF capacitors must be connected in parallel to store a charge of 1 C with a potential of 110 V across the capacitors?
View SolutionCalculate energy stored in a capacitor of 5μF when it is charged to a potential of 250 volt.
View SolutionThe energy stored in a capacitor of capacity C and potential V is given by
View SolutionIn the circuit shown in figure, the charge stored on a capacitor of capacitance 3μF is
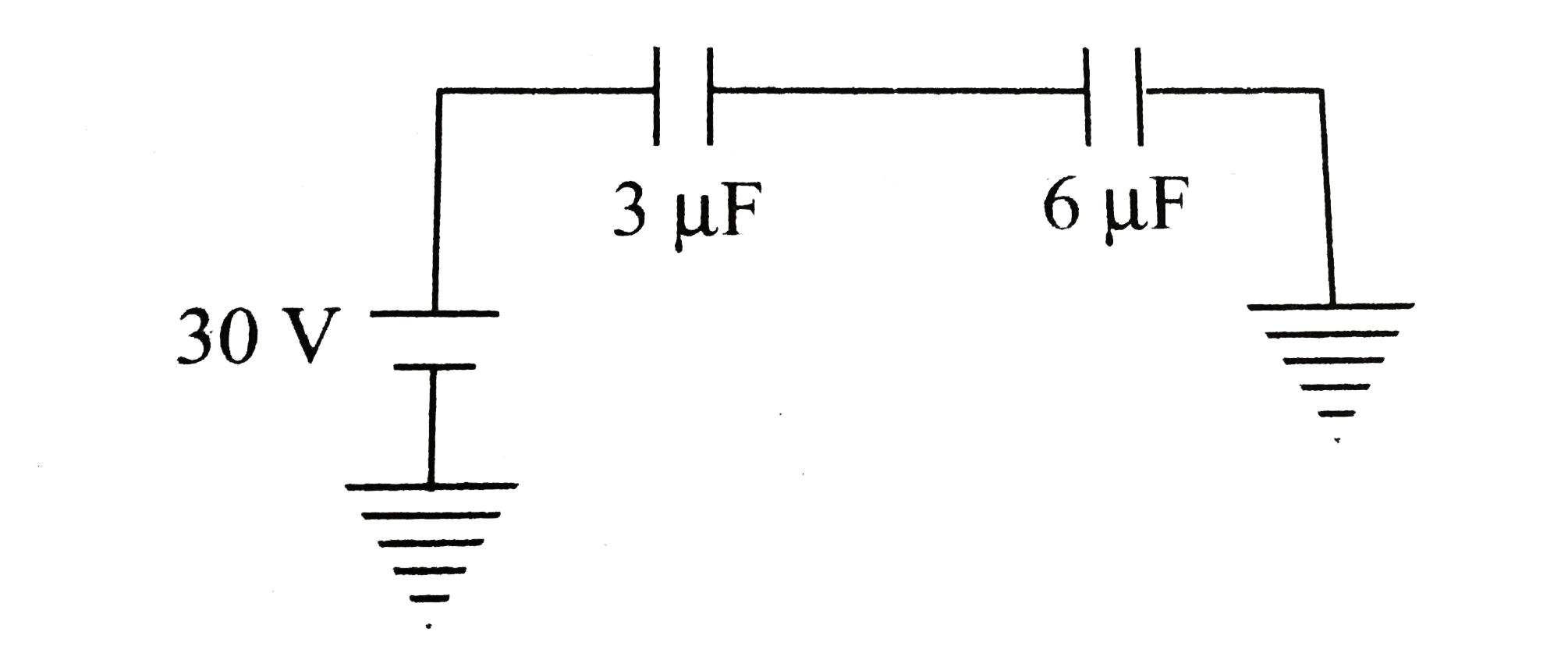
View SolutionIn the circuit shown in figure find

a. the equivalent capacitance
b. the charge stored in each capacitor and
c. the potential difference across each capacitor.
View Solution