Potential difference beween centre and surface of the sphere of radius R and uniorm volume charge density ρ within it will be
ρR26ε0
ρR24ε0
ρR23ε0
ρR22ε0
The correct Answer is:A
To find the potential difference between the center and the surface of a sphere of radius R with a uniform volume charge density ρ, we can follow these steps:
Step 1: Understand the formula for electric potential
The electric potential V at a distance r from the center of a uniformly charged sphere can be calculated using the formula:
V=KQr
where K=14πϵ0 and Q is the total charge enclosed within the sphere.
Step 2: Calculate the total charge Q
The total charge Q of the sphere can be calculated using the volume charge density ρ:
Q=ρ⋅Vsphere=ρ⋅(43πR3)
Step 3: Substitute Q into the potential formula
Now, substituting Q into the potential formula, we get:
V=K⋅ρ⋅(43πR3)r
Step 4: Calculate the potential at the center Vc
For the center of the sphere (where r=0), the potential is given by:
Vc=32⋅KQR
Substituting Q:
Vc=32⋅K⋅ρ⋅(43πR3)R=2KρπR2
Step 5: Calculate the potential at the surface Vs
For the surface of the sphere (where r=R), the potential is:
Vs=KQR=K⋅ρ⋅(43πR3)R=43KρπR2
Step 6: Find the potential difference Vc−Vs
Now, we can find the potential difference between the center and the surface:
Vc−Vs=(2KρπR2)−(43KρπR2)
Step 7: Simplify the expression
To simplify:
Vc−Vs=KρπR2(2−43)=KρπR2(63−43)=KρπR2⋅23
Step 8: Final expression for potential difference
Substituting K=14πϵ0:
Vc−Vs=14πϵ0⋅ρ⋅R2⋅23=ρR26ϵ0
Thus, the potential difference between the center and the surface of the sphere is:
ΔV=ρR26ϵ0
The electric potential V at a distance r from the center of a uniformly charged sphere can be calculated using the formula:
V=KQr
where K=14πϵ0 and Q is the total charge enclosed within the sphere.
The total charge Q of the sphere can be calculated using the volume charge density ρ:
Q=ρ⋅Vsphere=ρ⋅(43πR3)
Now, substituting Q into the potential formula, we get:
V=K⋅ρ⋅(43πR3)r
For the center of the sphere (where r=0), the potential is given by:
Vc=32⋅KQR
Substituting Q:
Vc=32⋅K⋅ρ⋅(43πR3)R=2KρπR2
For the surface of the sphere (where r=R), the potential is:
Vs=KQR=K⋅ρ⋅(43πR3)R=43KρπR2
Now, we can find the potential difference between the center and the surface:
Vc−Vs=(2KρπR2)−(43KρπR2)
To simplify:
Vc−Vs=KρπR2(2−43)=KρπR2(63−43)=KρπR2⋅23
Substituting K=14πϵ0:
Vc−Vs=14πϵ0⋅ρ⋅R2⋅23=ρR26ϵ0
ΔV=ρR26ϵ0
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
The magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View SolutionA smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?
 View Solution
View SolutionThe electric potential due to uniformly charged sphere of radius R,having volume charge density rho having a spherical cavity of radius R2 as shown as in figure at point p is
_PHY_E05_288_Q01.png) View Solution
View SolutionPotential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
View SolutionA hollow charged metal sphere has radius r. If the potential difference between its surface and a point at a distance 3r from the centre is V, then electric field intensity at a distance 3r is
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is
 View Solution
View SolutionA ring of radius R is placed in the plane its centre at origin and its axis along the x-asis and having uniformly distributed positive charge. A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velcity , then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represent by :
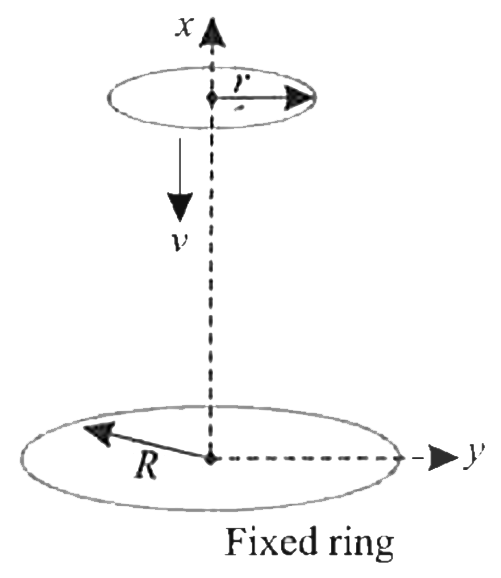 View Solution
View SolutionTwo non-conducting solid spheres of radii R and 2R, having uniform volume charge densities ρ1 and ρ2 respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centres of the spheres, is zero. The ratio ρ1ρ2 can be
View SolutionA solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionA charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius alpha. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and the outer surface?
View Solution

