Two blocks of masses m and 3m on a horizontal surface are in contact with the ends of a horizontal massless spring. The coefficient of friction between m and surface and between 3m and surface is μ and μ/3 respectively. The two blocks are moved towards each other to compress the spring and then released. The two blocks move off in opposite directions covering distances S1 and S2 before comming to rest. S1:S2 is
1:9
1:3
3:1
9:1
The correct Answer is:C
To solve the problem, we need to analyze the motion of two blocks, one with mass m and the other with mass 3m, after they are released from a compressed spring. We will derive the ratio of the distances S1 and S2 that the blocks travel before coming to rest.
1. Understanding the System:
- We have two blocks: Block A with mass m and Block B with mass 3m.
- The coefficients of friction are μ for Block A and μ3 for Block B.
2. Conservation of Momentum:
- Initially, both blocks are at rest, so the initial momentum Pi=0.
- When released, let V1 be the velocity of Block A and V2 be the velocity of Block B.
- By conservation of momentum:
mV1=3m(−V2)⟹V1=3V2
3. Frictional Forces:
- The frictional force FA on Block A is:
FA=μmg
- The frictional force FB on Block B is:
FB=μ3⋅3mg=μmg
4. Acceleration due to Friction:
- For Block A:
ma1=μmg⟹a1=μg
- For Block B:
3ma2=μmg⟹a2=μg3
5. Using Kinematic Equations:
- For Block A (initial velocity V1, final velocity 0):
0=V21−2a1S1⟹S1=V212a1=V212μg
- For Block B:
0=V22−2a2S2⟹S2=V222a2=V222⋅μg3=3V222μg
6. Finding the Ratio S1:S2:
- Substitute V1=3V2 into the equation for S1:
S1=(3V2)22μg=9V222μg
- Now, we can find the ratio:
S1S2=9V222μg3V222μg=93=3
- Thus, the ratio S1:S2=3:1.
Final Answer:
The ratio S1:S2 is 3:1.
- We have two blocks: Block A with mass m and Block B with mass 3m.
- The coefficients of friction are μ for Block A and μ3 for Block B.
- Initially, both blocks are at rest, so the initial momentum Pi=0.
- When released, let V1 be the velocity of Block A and V2 be the velocity of Block B.
- By conservation of momentum:
mV1=3m(−V2)⟹V1=3V2
- The frictional force FA on Block A is:
FA=μmg
- The frictional force FB on Block B is:
FB=μ3⋅3mg=μmg
- For Block A:
ma1=μmg⟹a1=μg
- For Block B:
3ma2=μmg⟹a2=μg3
- For Block A (initial velocity V1, final velocity 0):
0=V21−2a1S1⟹S1=V212a1=V212μg
- For Block B:
0=V22−2a2S2⟹S2=V222a2=V222⋅μg3=3V222μg
- Substitute V1=3V2 into the equation for S1:
S1=(3V2)22μg=9V222μg
- Now, we can find the ratio:
S1S2=9V222μg3V222μg=93=3
- Thus, the ratio S1:S2=3:1.
The ratio S1:S2 is 3:1.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
Two blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between m1 and platform is 2μ and that between block m2 and platform is μ.The platform moves with an acceleration a . The normal reation between the blocks is

View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
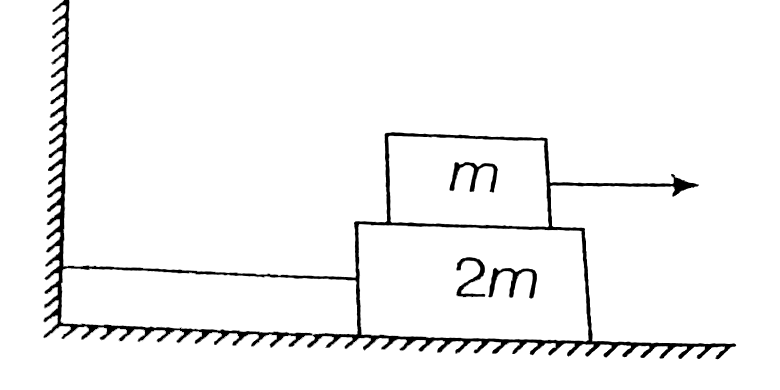
View SolutionTwo blocks of masses m and 2 m are placed one over the other as shown in figure.The coefficient of friction between m and 2m is μ and between 2m and ground is μ3. If a horizontal force F is applied on upper block and T is tension developed in string, then choose the incorrect alternative.
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
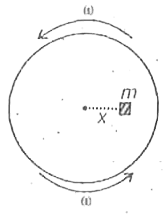
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionTwo blocks of mass m and 2m are arranged on a wedge that is fixedd on a horizontal surface. Friction coefficient between the block and wedge are shown . Find the magnitude of acceleration of two blocks.

View SolutionA block of mass m is placed behind in contact with vertical side of M as shown in the figure. The coefficient of static friction between m and M in μ. The least horizontal force with which m can be pushed so that the two blocks move together is (neglect friction between M and ground).
View Solution
