ABCD is a quadrilateral whose diagnonal AC divides it into two parts, equal in area, then ABCD
is a rectangle
is always is rhombus
is a parallelogram
need not be any of (a), (b) or (c)
The correct Answer is:D
To solve the problem, we need to determine the nature of the quadrilateral ABCD given that its diagonal AC divides it into two parts of equal area.
1. Understanding the Problem:
We are given a quadrilateral ABCD, and we know that the diagonal AC divides it into two triangles, ΔABC and ΔADC, which have equal areas.
2. Area of Triangles:
The area of triangle ΔABC is given by the formula:
AreaΔABC=12×base×height
Similarly, for triangle ΔADC:
AreaΔADC=12×base×height
3. Equal Areas:
Since the areas of the two triangles are equal, we can set up the equation:
AreaΔABC=AreaΔADC
This implies:
12×baseABC×heightABC=12×baseADC×heightADC
4. Properties of Quadrilaterals:
For a quadrilateral to have its diagonal dividing it into two equal areas, it can be a rectangle, rhombus, or parallelogram. All these shapes have the property that their diagonals bisect each other and divide the shape into two equal areas.
5. Conclusion:
Since the question states that the diagonal AC divides the quadrilateral ABCD into two equal areas, ABCD can be a rectangle, rhombus, or parallelogram. However, it does not necessarily have to be any of these shapes; it could also be any other quadrilateral that satisfies this condition.
6. Final Answer:
Therefore, the correct conclusion is that quadrilateral ABCD need not be any of the specified shapes (rectangle, rhombus, or parallelogram). Hence, the answer is option 4: "need not be any of A, B, and C".
We are given a quadrilateral ABCD, and we know that the diagonal AC divides it into two triangles, ΔABC and ΔADC, which have equal areas.
The area of triangle ΔABC is given by the formula:
AreaΔABC=12×base×height
Similarly, for triangle ΔADC:
AreaΔADC=12×base×height
Since the areas of the two triangles are equal, we can set up the equation:
AreaΔABC=AreaΔADC
This implies:
12×baseABC×heightABC=12×baseADC×heightADC
For a quadrilateral to have its diagonal dividing it into two equal areas, it can be a rectangle, rhombus, or parallelogram. All these shapes have the property that their diagonals bisect each other and divide the shape into two equal areas.
Since the question states that the diagonal AC divides the quadrilateral ABCD into two equal areas, ABCD can be a rectangle, rhombus, or parallelogram. However, it does not necessarily have to be any of these shapes; it could also be any other quadrilateral that satisfies this condition.
Therefore, the correct conclusion is that quadrilateral ABCD need not be any of the specified shapes (rectangle, rhombus, or parallelogram). Hence, the answer is option 4: "need not be any of A, B, and C".
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.2 Very Short Answer Type Questions5videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.3 Short Answer Type Questions9videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.414videos
CIRCLES
Similar Questions
ABCD is a quadrilateral whose diagnonal AC divides it into two parts, equal in area, then ABCD
View SolutionThe diagonal AC of a quadrilateral ABCD divides it into two triangles of equal areas. Prove that diagonal AC bisects the diagonal BD.
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.
 View Solution
View SolutionIn the quadrilateral ABCD, the diagonals AC and BD are equal and perpendicular to each other. What type of a quadrilateral is ABCD?
View SolutionFind the area of a quadrilateral ABCD whose diagonal AC is 25 cm long and the lengths of perpendiculars from opposite vertices B and D on AC are BE = 3.6 cm and DF = 2.4 cm .
 View Solution
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionIn a cyclic quadrilateral ABCD the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
View SolutionIn Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
are of ΔABP= area of □ABCD
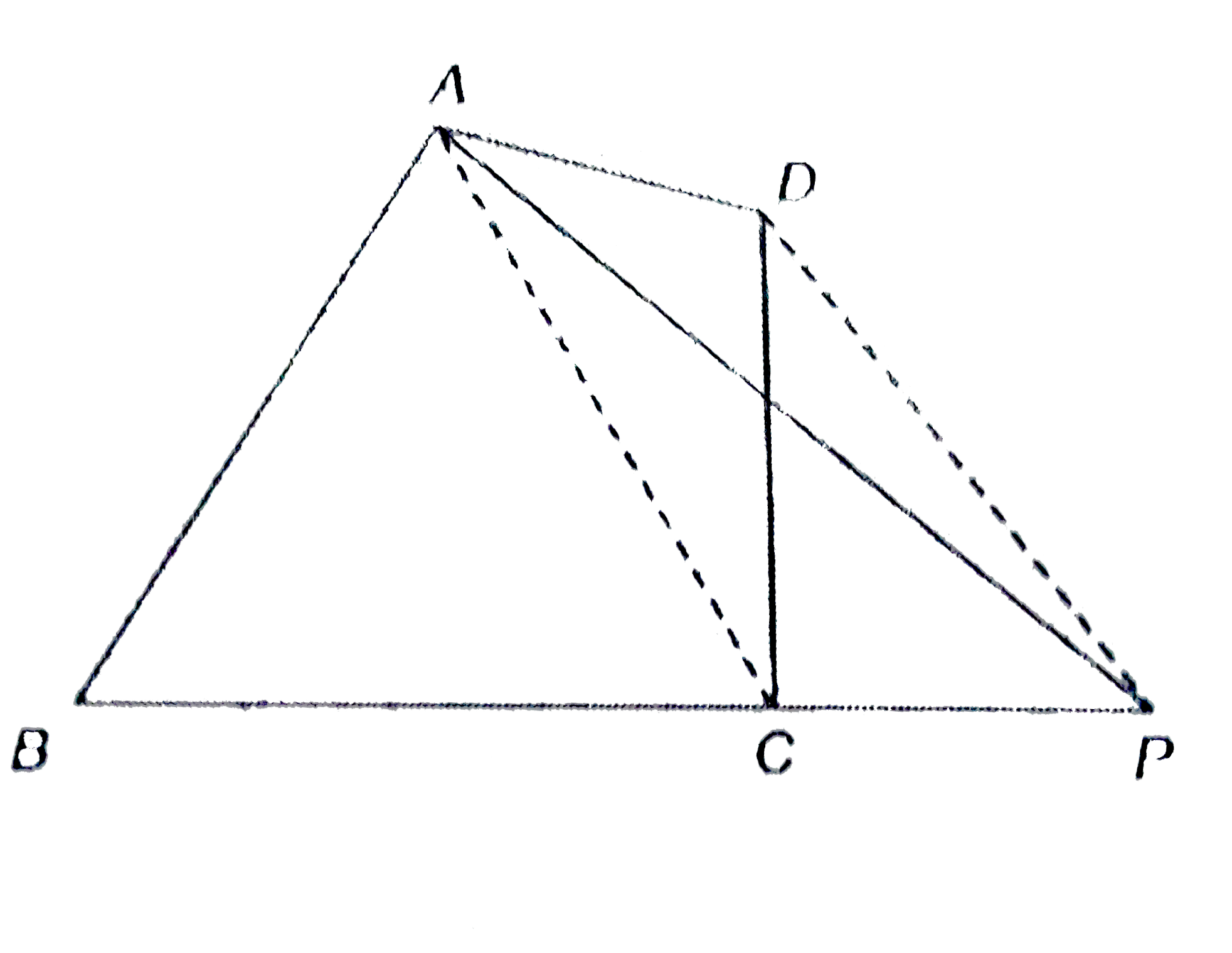 View Solution
View Solution
