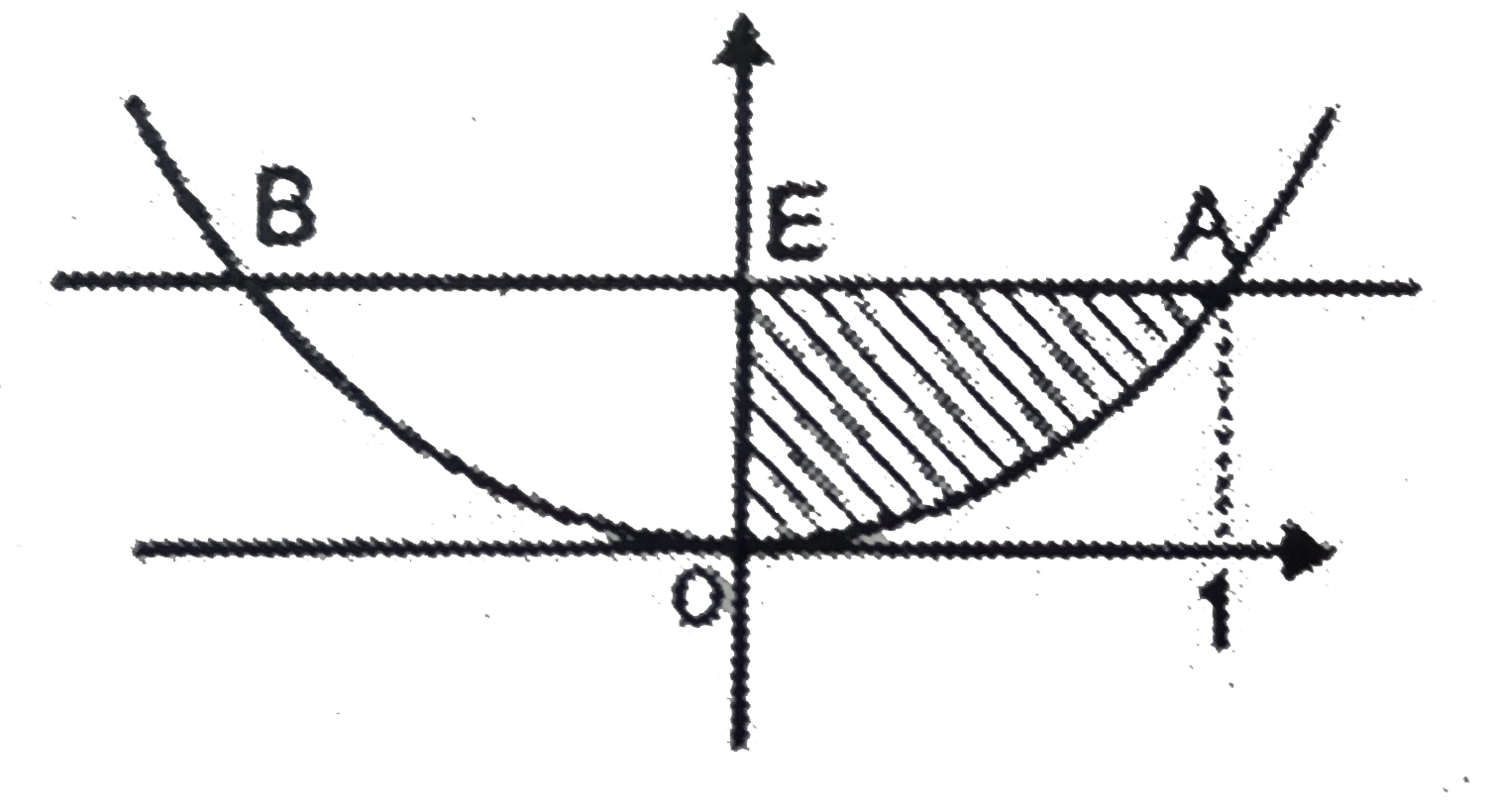
Find the area bounded by the parabola y2=4ax and the line y=2ax.
y2=4aξmpliesy=2√a√x ...(1)
y=2ax ...(2)
On solving the eqs. (1) and (2), we get the points of intersection are O(0 , 0) and P(1a,2)
Draw PQ ⊥ OX

Now the area of the region bounded by the parabola and the straight line
= Area of OQPAO - Area of OQPBO
=∫1/a0√a√xdx−∫1/a02axdx
=2√a.[23x3/2]1/a0−2a[x22]1/a0
=43√a.1a3/2−a.1a2
=43a−1a=13asq. units.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8a28videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8 B Multiple Choice Questions10videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
Area bounded by the parabola y2=x and the line 2y=x is:
View SolutionFind the area bounded by the parabola x2=y, x-axis and the line y=1
 View Solution
View SolutionIf the area bounded by the parabola y2=4ax and the line y=mx is a212 sq. units, by using integration find the value of m.
View SolutionFind the area bounded by the parabola y2=4x and the straight line x+y=3.
View SolutionFind the area bounded by the parabola x2=y and line y=1.
View SolutionFind the area bounded by the parabola y2=4ax and its latus rectum.
View SolutionFind the area bounded by the parabola y=2−x2 and the straight line y+x=0.
View SolutionFind the area bounded by the parabola y=x2, the x -axis and the lines x=−1,x=2 .
View SolutionUsing integration, find the area of the region bounded by the parabola y2=4x and the line x=4.
View SolutionFind the area of the region bounded by: the parabola y=x2 and the line y=x
View Solution

