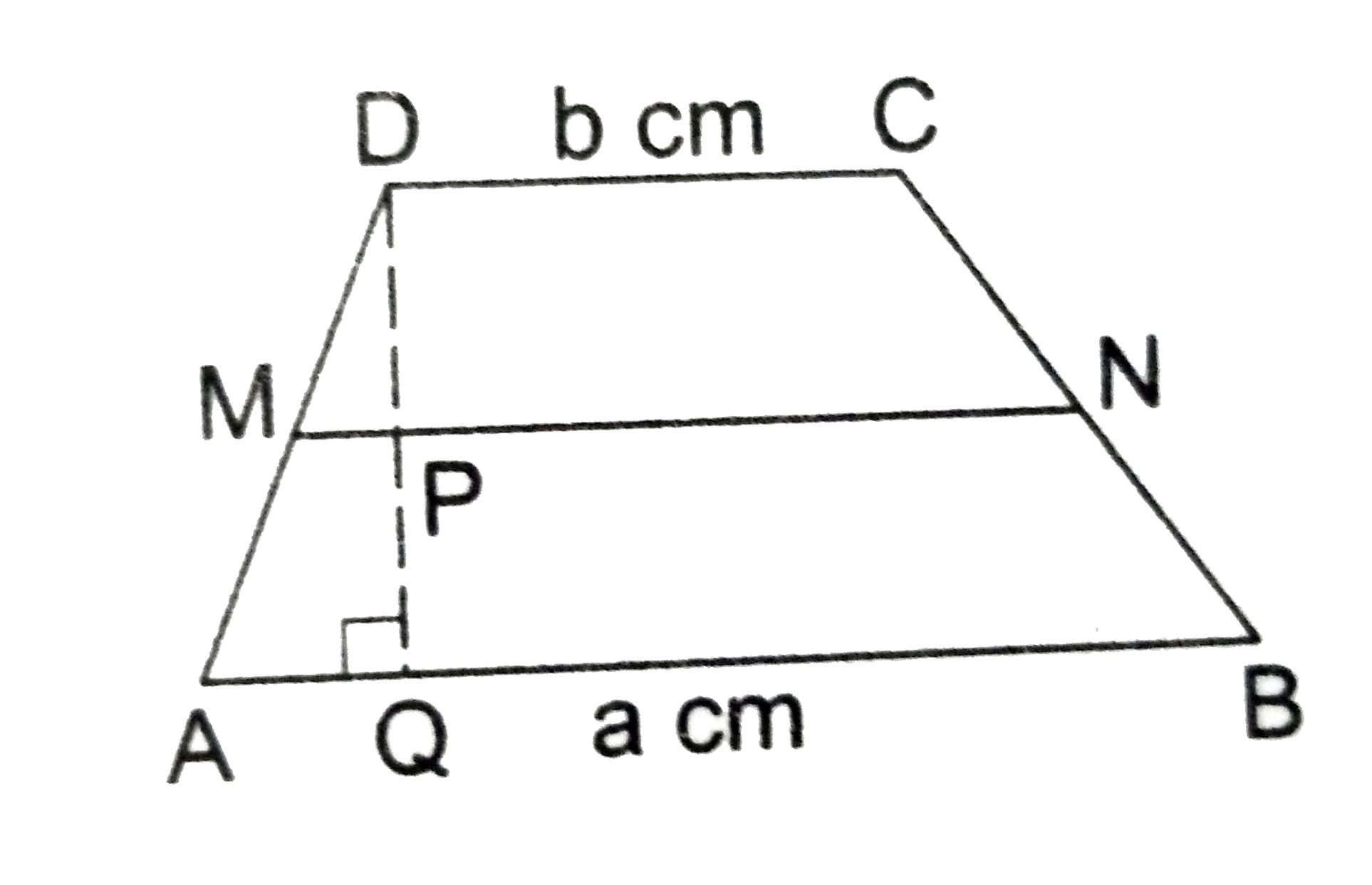
In a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA).
The correct Answer is:(a+3b):(3a+b)
M and N are midpoints of AD and BC respectively
⇒ MN||AB||DC and MN =12(AB+DC)=(a+b2).
Draw DQ⊥AB. Let DQ cut MN at P.
Then, P is the midpoint of DQ,
i.e., DP = PQ = h (say).
Now, ar(DCNM)=12×(DC+MN)×DP=12=12×(b+a+b2)×h=h4×(a+3b)
and ar(MNBA)=12×(MN+AB)×PQ=12×(a+b2+a)×h=h4×(3a+b).
∴ar(DCNM):ar(MNBA)=(a+3b):(3a+b).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
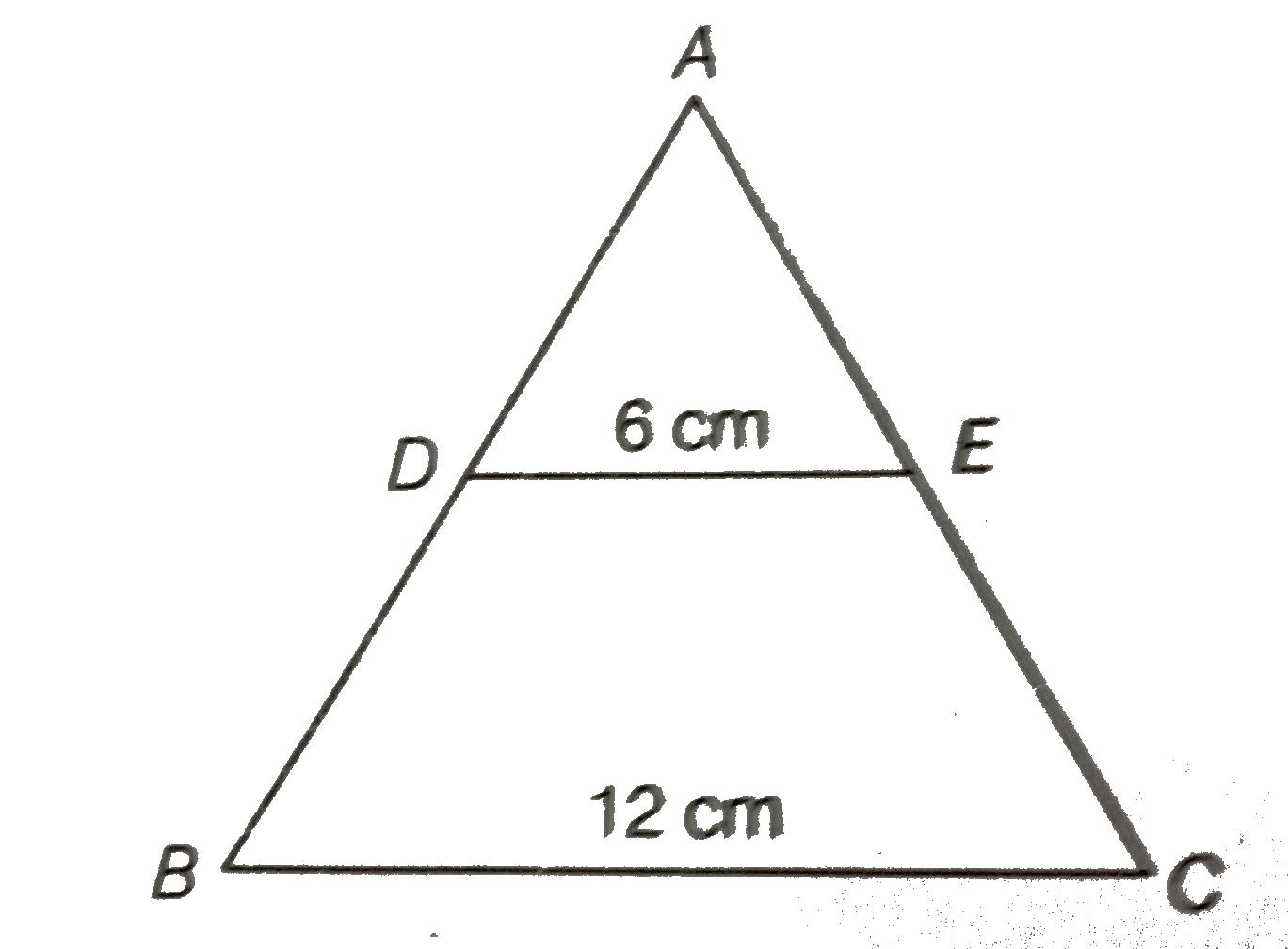
In figure, if DE||BC, then find the ratio of ar (ΔADE) and ar(DECB).
 A1:3B1:2C2:5D3:5
A1:3B1:2C2:5D3:5ABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

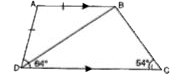
XY=A40 cmB50 cmC60 cmD30 cmIn a trapezium ABCD, AB||DC, AB = AD, ∠ADC=64∘and∠BCD=54∘. Find ∠DBC.
 A64∘B72∘C94∘D116∘
A64∘B72∘C94∘D116∘
ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View SolutionABCD is a trapezium in which AB || DC, AB = 16 cm and DC = 24 cm. If E and Fare respectively the midpoints of AD and BC, prove that ar(ABFE) = 911 ar(EFCD).
View SolutionABCD is trapezium in which AB∣∣DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
ar(DCYX)=79ar(XYBA).
View SolutionIn a trapezium ABCD, DC || AB , AB = 12 cm and DC = 7.2 cm. What is the length of the line segment joining the mid- points of its diagonals?
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogramABCD. Show that ar (APB) = ar (BQC).
View Solution
