In the given figure, AB is a diameter of a circle with centre O and DO∣∣CB.
In ∠BCD=120∘, calculate
(i)∠BAD , (ii) ∠ABD
(iii) ∠CBD, (iv) ∠ADC
Also, show that ΔAOD is an equilateral triangle.
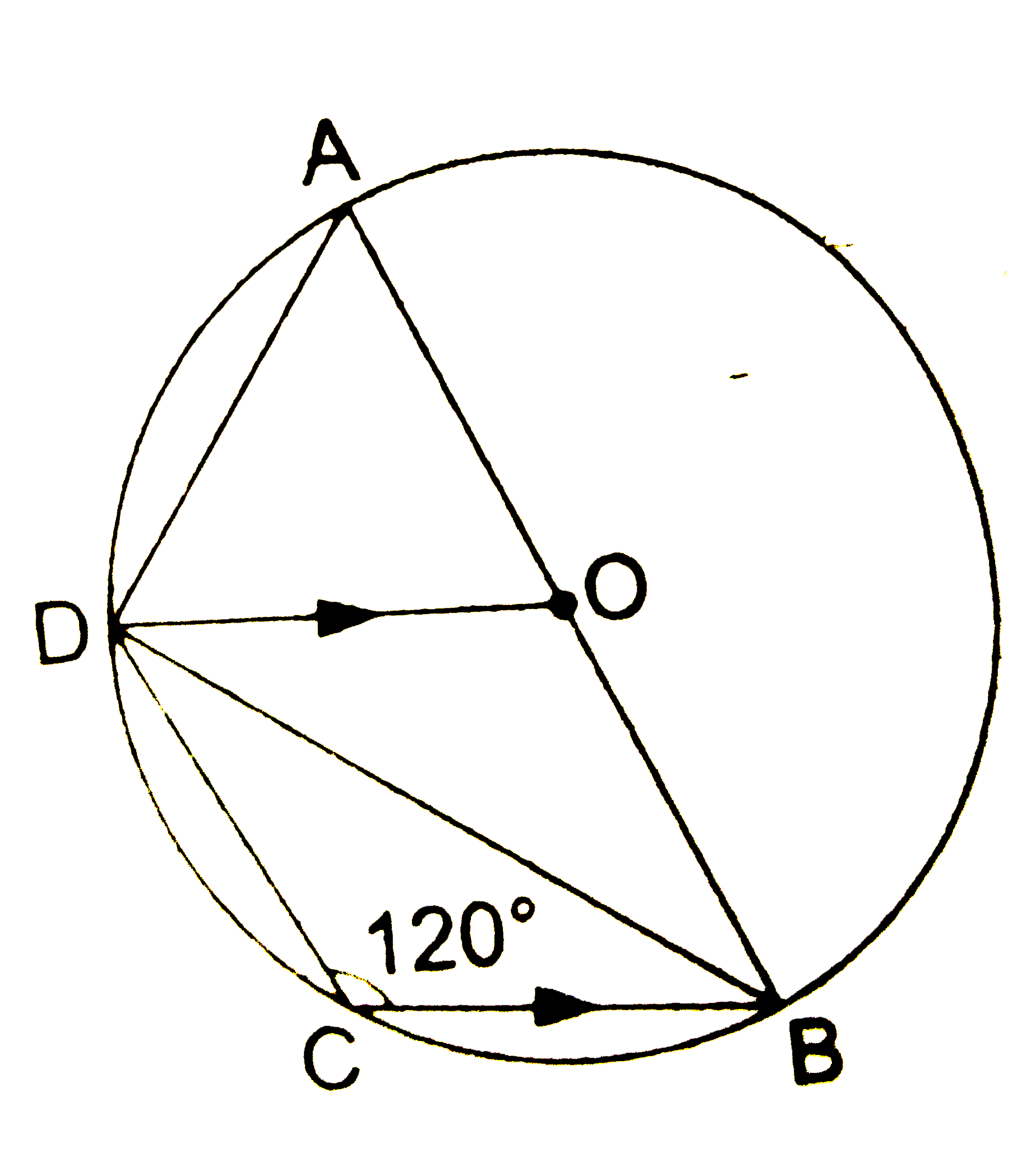
The correct Answer is:(i)∠BAD=60∘,(ii)∠ABD=30∘,(iii)∠CBD=30∘,(iv)∠ADC=120∘
∠BCD+∠BAD=180∘⇒BAD=60∘
∠BAD=90∘ [ angle in a semicircle ]
∠BDA+∠BAD+∠ABD=180∘⇒∠ABD=30∘
OD=OA⇒∠ODA=∠OAD=∠BAD=60∘
∴∠ODB=90∘−∠ODA=30∘
∴∠CBD=∠ODB=30∘⇒∠CDB=180∘−(120∘+30∘)=30∘
and ∠ADC=∠ADB+∠CDB=(90∘+30∘)=120∘
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)5videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)37videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B18videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
Similar Questions
In the given figure, AB is a diameter of the circle with centre O and DO||CB.If ∠BCD=120∘,calculate 1. ∠BAD 2. ∠ABD 3. ∠CBD 4. ∠ADC Also show that AOD is an equilateral triangle
View SolutionIn the given figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘, find ∠ATQ.
View Solution
Knowledge Check
- Question 1 - Select One
In the given figure, BOD is the diameter of the circle with centre O. ∠COD=92∘and∠ABD=65∘. Then y equals
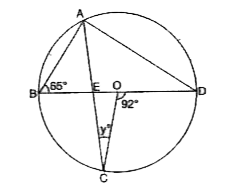 A65∘B46∘C44∘D21∘
A65∘B46∘C44∘D21∘ - Question 2 - Select One
AB is a diameter of the circle with centre O, CD is chord of the circle. If ∠BOC=120∘, then the value of ∠ADC is
A42∘B30∘C60∘D35∘
In the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
View SolutionIn the giben figure, AB is the diameter of the circle, with centre O and AT is the tangent. Calculate the calue of x.
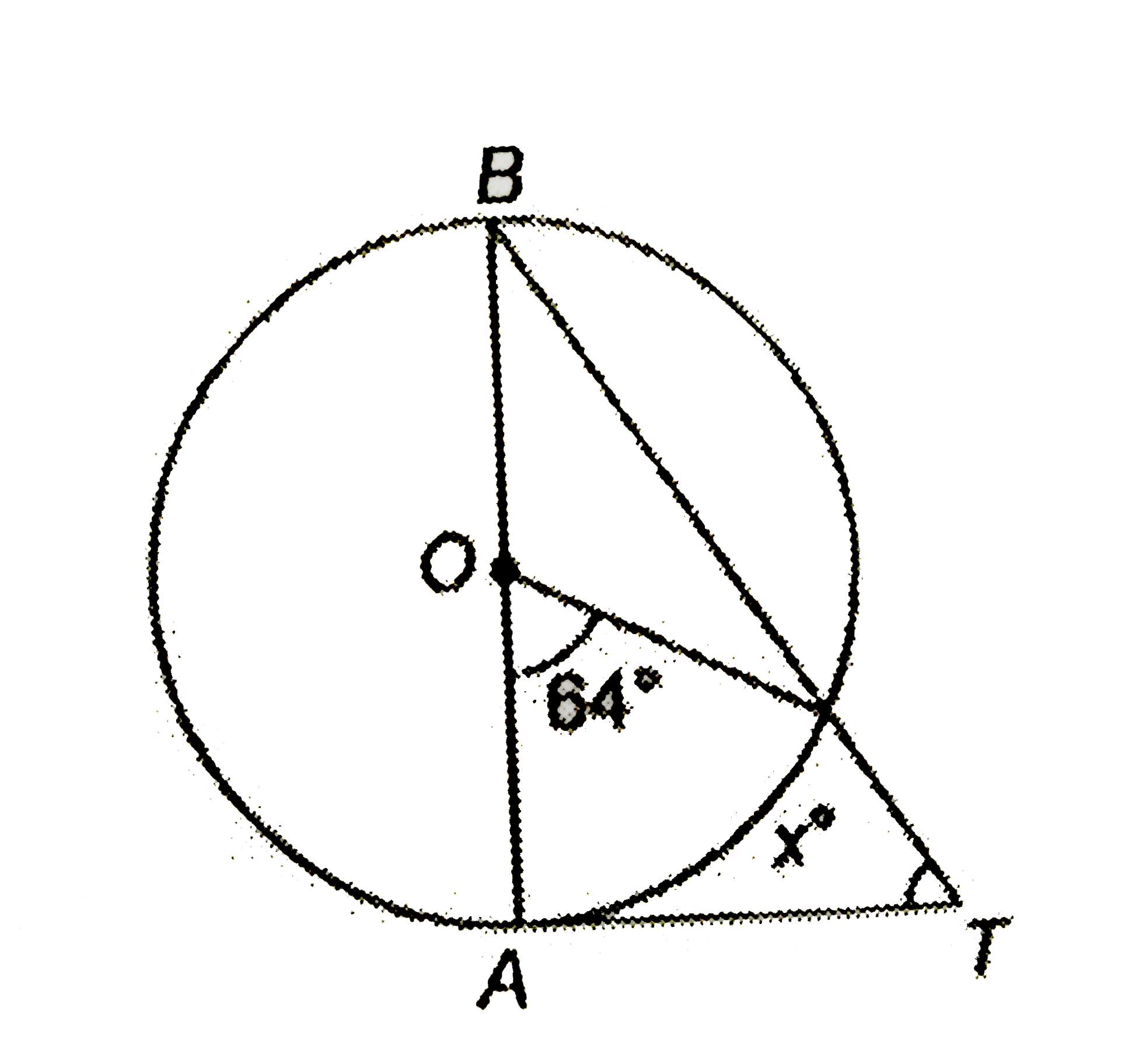 View Solution
View SolutionIn the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
View SolutionIn the given figure, AB is the diameter of the circle. ∠ADC=120∘. Find ∠CAB :
 View Solution
View SolutionIn the given fig. OP is equal to the diameter of the circle with centre O. Prove that ΔABP is an equilateral triangle.
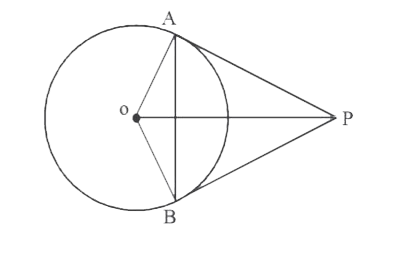 View Solution
View SolutionIn the figure, ABC is a triangle inscribed in a circle with centre O.
If AB = AC = 15 cm and BC = 5 cm, calculate the radius of the circle.View Solution

