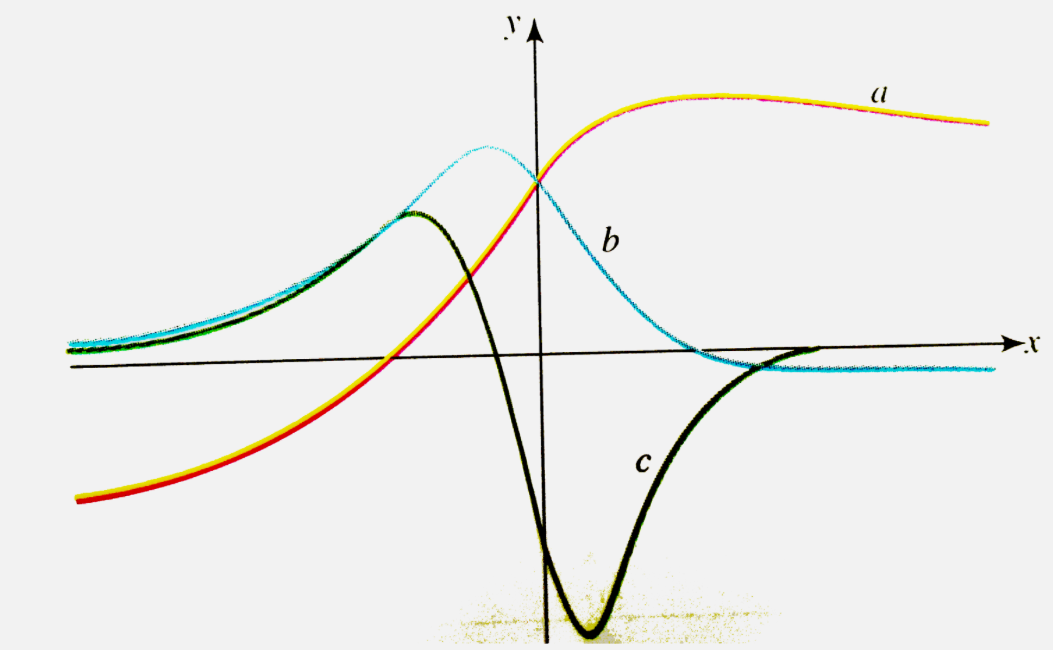
The figure shows the graphs of f, f' and f'' . Identify each curve and explain your choices.
(##CEN_GRA_C01_S01_025_Q01.png" width="80%">
Text Solution
Clearly the graph 'a' and 'b' are lying entirely above the x-axis. Now for graph 'b', derivative becomes zero at point p.

For graph 'c', derivative becomes zero at x = q and x = r.
Now none of the graphs meets the x-axis at two points q and r.
Hence 'a' must be the graph of the derivative of graph 'b'. Also for x = p, the graph of 'a' meets the x-axis , which confirms this fact.
Let 'b' be the graph of y = f(x) and 'a' be the graph of y = f'(x) , then can 'c' be the graph of y = f''(x)?
Certainly not, as otherwise graph 'c' had cut the x-axis twice.
So 'c' is the graph of y=f(x). 'b' is the graph of y = f'(x) and 'a' is the graph of y = f''(x).
Also for graph 'c', the angle of tangent with + ve x -axis is acute and increases till the point x = p. After x = p and onwards, angle decreases but remains positive. Thus, the graph of y = f'(x) , which is graph is graph 'b' , line entirely above the x-axis. In other words. the graph of 'c' is entirely increasing, hence its derivative is positive, as a result graph 'b', which is the graph of y = f'(x), lies above x - axis.
So finally c is y = f(x), b is y = f'(x) and a = f'(x).
|
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise
18 Videos
- FUNCTIONSBOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Question Bank
30 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
Similar Questions
Knowledge Check
In figure ,PR = ?
(##CEN_JEE_MAT_X_C14_E01_032_Q01.png" width="80%">A20 cmB22 cmC24 cmD26 cmIn the figure shown
(##AHT_PGT_PHY_C10_E01_006_Q01.png" width="80%">AP>P0BP<P0CP=P0DP=0(##SASA_NJA_OBJ_BIO_V02_C04_E03_039_Q01.png" width="80%">
A(A)(B)(C)(D)iiiiviiiB(A)(B)(C)(D)iviiiiiiC(A)(B)(C)(D)iviiiiiiD(A)(B)(C)(D)iiiiiivi
The graph of y = f(x) is shown, find the number of solution of f(f(x)) = 2.
(##CEN_GRA_C01_S01_007_Q01.png" width="80%">
View SolutionDoes the graph below represent a function or a relation?
(##CEN_GRA_C01_S01_002_Q01.png" width="80%">
View SolutionThe graph of the second derivation f''(x) is given in the following figure. State the x - coordinate of the point of inflection of f. Given reasons for your answer.
(##CEN_GRA_C01_S01_024_Q01.png" width="80%">
View SolutionIn the following graph, state the absolute and local maximum and minimum values of the function.
(##CEN_GRA_C01_S01_022_Q01.png" width="80%">
View SolutionWrite IUPAC name :
" "(##U_LIK_SP_CHE_XII_C13_E08_056_Q01.png" width="80%">
View Solution