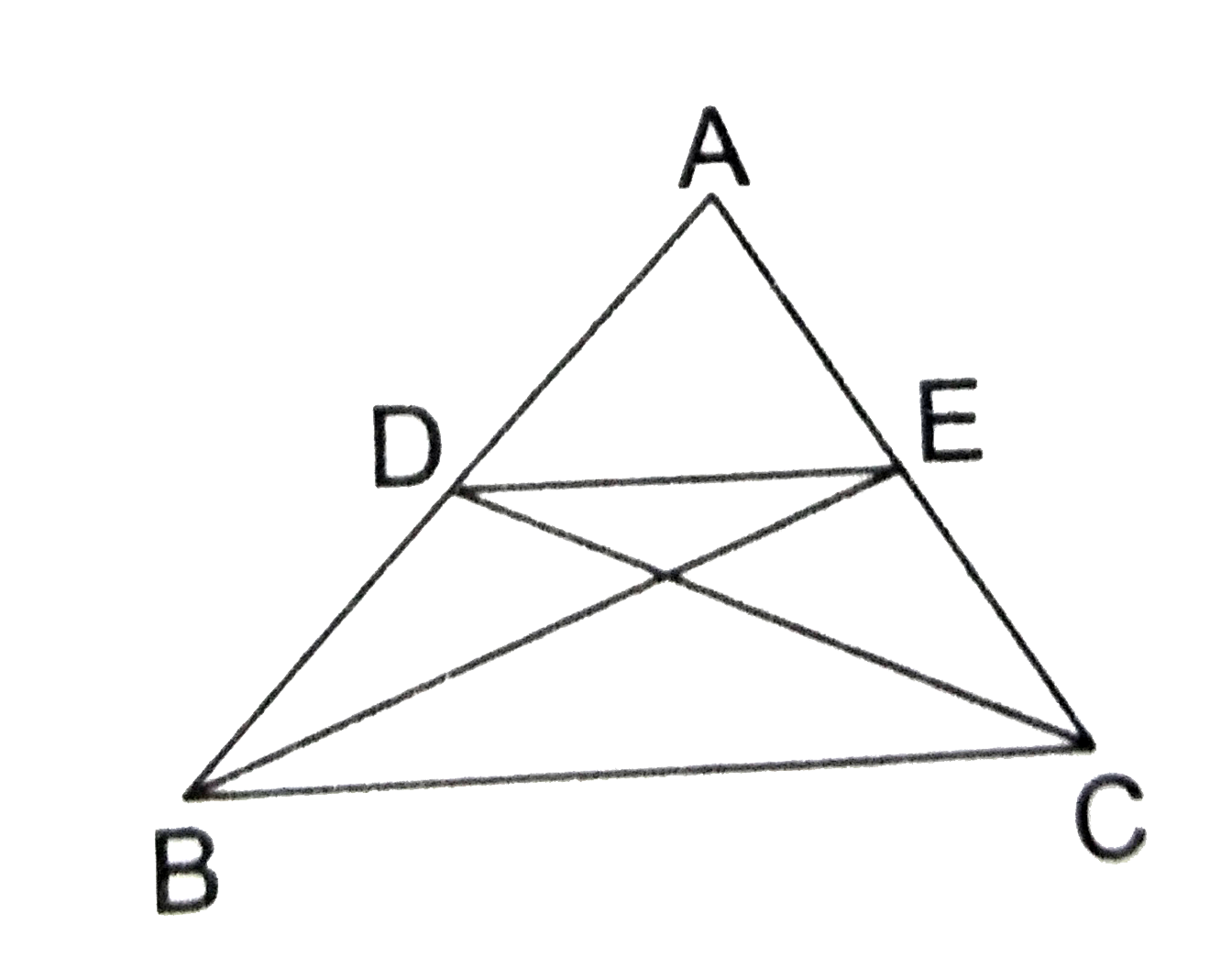
The points D and E are respectively located on AB and AC on the sides of ΔABC such that ar(DBC)=ar(EBC). Demonstrate thatDE∣∣BC.
△BCEand△BCD are on the same base BC and have equal area. So, their corresponding altitudes must be equal.
∴ DE||BC.
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
If D, E, F are respectively the mid-points of AB, AC and BC respectively in a ΔABC, then −−→BE+−−→AF=
A−−→DCB12−−→BFC2−−→BFD32−−→BF
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(BDEF) =12ar(△ABC)
View SolutionIf D, E and F are respectively, the mid-points of AB, AC and BC in ΔABC, then BE + AF is equal to
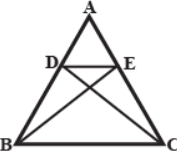
View SolutionIn Figure, D,E are points on sides AB and AC respectively of ABC, such that ar(BCE)=ar(BCD). Show that DEBC.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC

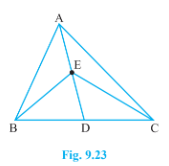
View SolutionIn Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
ar(ΔPRQ) = 1/2 ar(ΔARC)
View Solution
