Complete Solutions to JEE Main And Advanced of chapter MECHANICAL PROPERTIES OF MATTER AND FLUIDS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MECHANICAL PROPERTIES OF MATTER AND FLUIDS |
| SUNIL BATRA | JEE Main And Advanced |
| Number Of Questions | 78 |
| Academic Year | 2023-24 |
A wire of length L and cross sectional area A is made of a material of Young's modulus Y. If the wire is streched by an amount x, the work done is………………
View SolutionA solid sphere of radius R made of a material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless pistion of area A floats on the surface of the liquid. When a mass M is placed on the piston to compress the liquid the fractional change in the radius of the sphere, `deltaR//R`, is .............
View SolutionA piece of metal floats on mercury. The coefficients of volume expansion of the metal and mercury are `gamma_1` and `gamma_2` respectively. If the temperatures of both mercury and the metal are increased by an amount `DeltaT`, the fraction of the volume of the metal submerged in mercury changes by the factor............
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the pipe, where the cross- sectional area is `10cm^2`, the water velocity is `1ms^-1` and the pressure is 2000 Pa. The pressure of water at another point where the cross-sectional area is `5cm^2`, is........Pa. (Density of water `=10^3kg.m^-3`)
View SolutionA man is sitting in a boat which is floating in a pond. If the man drinks some water from the pond, the level of water in the pond decreases.
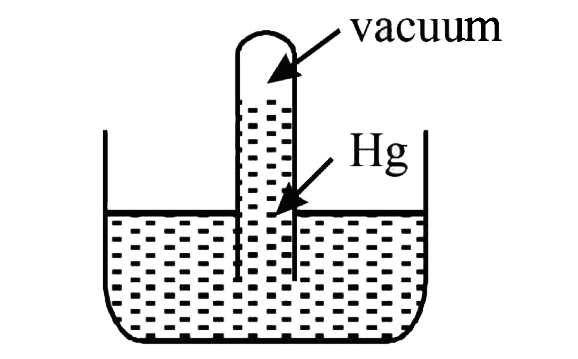
View SolutionA barometer made of very narrow tuve (see fig) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is `0.00018per C^@` and that of the tube is negligible. The temperature of mercury in the barometer is now raised by `1^@C`, but the temperature of the atmosphere does not raised by `1^@C`, but the temperature of the atmosphere does not change. Then the mercury height in the tube remains unchanged.
View SolutionWater in a closed tube (see fig) is heated with one arm vertically placed above a lamp. Water will begin to circulate along the tube in counter-clockwise direction.
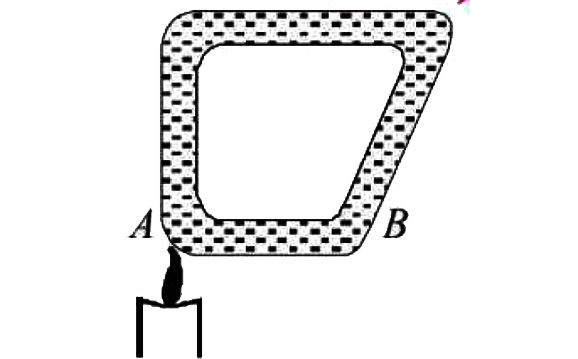
View SolutionA block of ice with a lead shot embedded in it is floating on water contained in a vessel. The temperature of the system is maintained at `0^@C` as the ice melts. When the ice melts completely the level of water in the vessel rises.
View SolutionA vessel containing water is given a constant acceleration 'a' towards the right along a straight horizontal path. Which of the following diagrams in Fig. represents the surface of the liquid?
View SolutionThe following four wires are made of the same material. Which of these will have the largest extension when the same tension is applied?
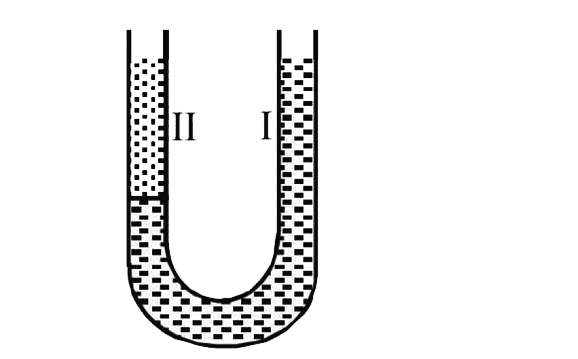
View SolutionA U-tube of uniform cross section (see figure) is partially filled with a liquid I. Another liquid II which does not mix with liquid I is poured into one side. It is found that the liquid levels of the two sides of the tube are the same, while the level of liquid I has risen by 2cm. If the specific gravity of liquid I is 1.1, the specific gravity of liquid II must be
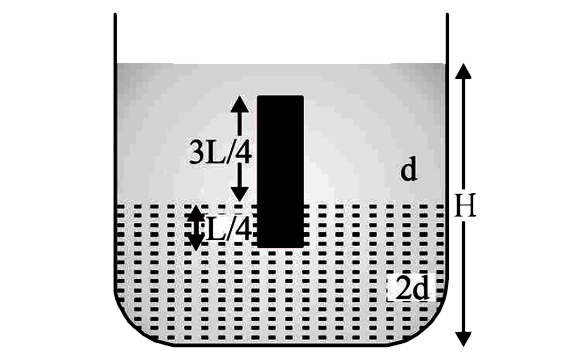
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure `P_0`. Then density D of solid is given by
View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density `rho` where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

View SolutionA wooden block, with a coin placed on its top, floats in water as shown in figure. The distance l and h are shown here. After some time the coin falls into water. Then

View SolutionThe adjacent graph shows the estension `(Deltal)` of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is `10^-6m^2`, calculate the Young's modulus of the material of the wire.
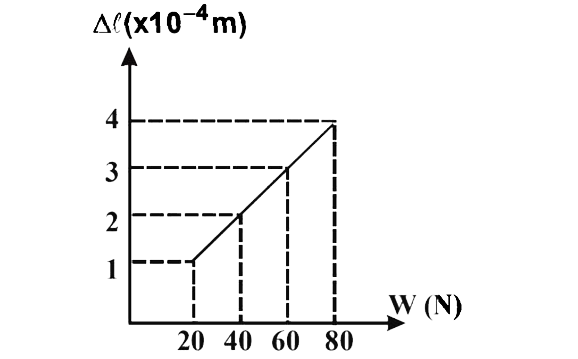
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If `a//A=0.1` then `v^2` is (where v is the velocity of water coming out of the hole)
View SolutionWhen temperature of a gas is `20^@C` and pressure is changed from `p_1=1.01xx10^5Pa` to `p_2=1.165xx10^5Pa` then the volume changed by `10%`. The bulk modulus is
View SolutionA glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,

View SolutionA thin uniform cylindrical shell, closed at both ends, is partially filled with water. It is floating vertically in water in half-submerged state. If `rho_c` is the relative density of the material of the shell with respect to water, then the correct statement is that the shell is
View SolutionOne end of a horizontal thick copper wire of length 2L and radius 2R is welded to an end fo another horizontal thin copper wire of lenth L and radius R. When the arrangement is stretched by applying forces at two ends, the ratio of the elongation in the thin wire to that in the thick wire is
View SolutionA glass capillary tube is of the shape of a truncated cone with an apex angle `alpha` so that its two ends have cross sections of different radii. When dipped in water vertically, water rises in it to a high h, where the radius of its cross section is b. If the surface tension of water is S, its density if `rho`, and its contact angle with glass is `theta`, the value of h will be (g is the acceleration due to gravity)

View SolutionA body floats in a liquid contained in a beaker. The whole system as shown in Figure falls freely under gravity. The upthrust on the body is

View SolutionThe spring balance A reads 2 kg with a block m suspended from it. A balance B reads 5kg when a beaker with liquid is put on the pan of the balance. The two balances are now so arranged that the hanging mass in inside the liquid in the beaker as shown in the figure. In this situation:
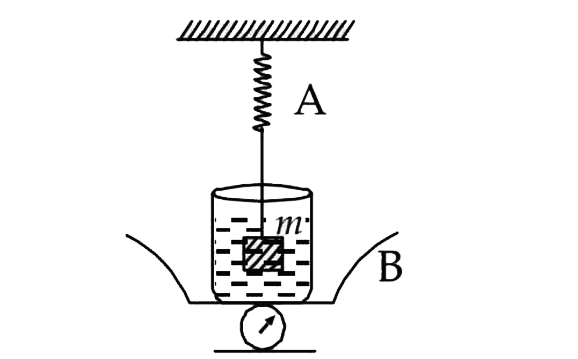
View SolutionA vessel contains oil (density `=0.8gm//cm^3`) over mercury (density `=13.6gm cm^3`). A homogeneous sphere floats with half its volume immersed in mercury and the other half in oil. The density of the material of the sphere in `gm//cm^3` is
View SolutionTwo rods of different materials having coefficients of thermal expansion `alpha_1`, `alpha_2` and Young's modulii `Y_1`, `Y_2` respectively are fixed between two rigid massive walls. The rods are heated such that they undergo the same increase in temperature. There is no bending of the rods. If `alpha_1:alpha_2=2:3`, the thermal stresses developed in the two rods are equal provided `Y_1:Y_2` is equal to
View SolutionWater from a tap emerges vertically downwards with an initial spped of `1.0ms^-1`. The cross-sectional area of the tap is `10^-4m^2`. Assume that the pressure is constant throughout the stream of water, and that the flow is steady. The cross-sectional area of the stream 0.15 m below the tap is
View SolutionA solid sphere of radius R and density `rho` is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density `3rho`. The complete arrangement is placed in a liquid of density `2rho` and is allowed to reach equilibrium. The correct statements(s) is (are)
View SolutionIn plotting stress versus strain curves for two material P and Q, a student by mistake puts strain on the y-axis stress on ther x-axis as shown in the figure. Then the correct statement is/are
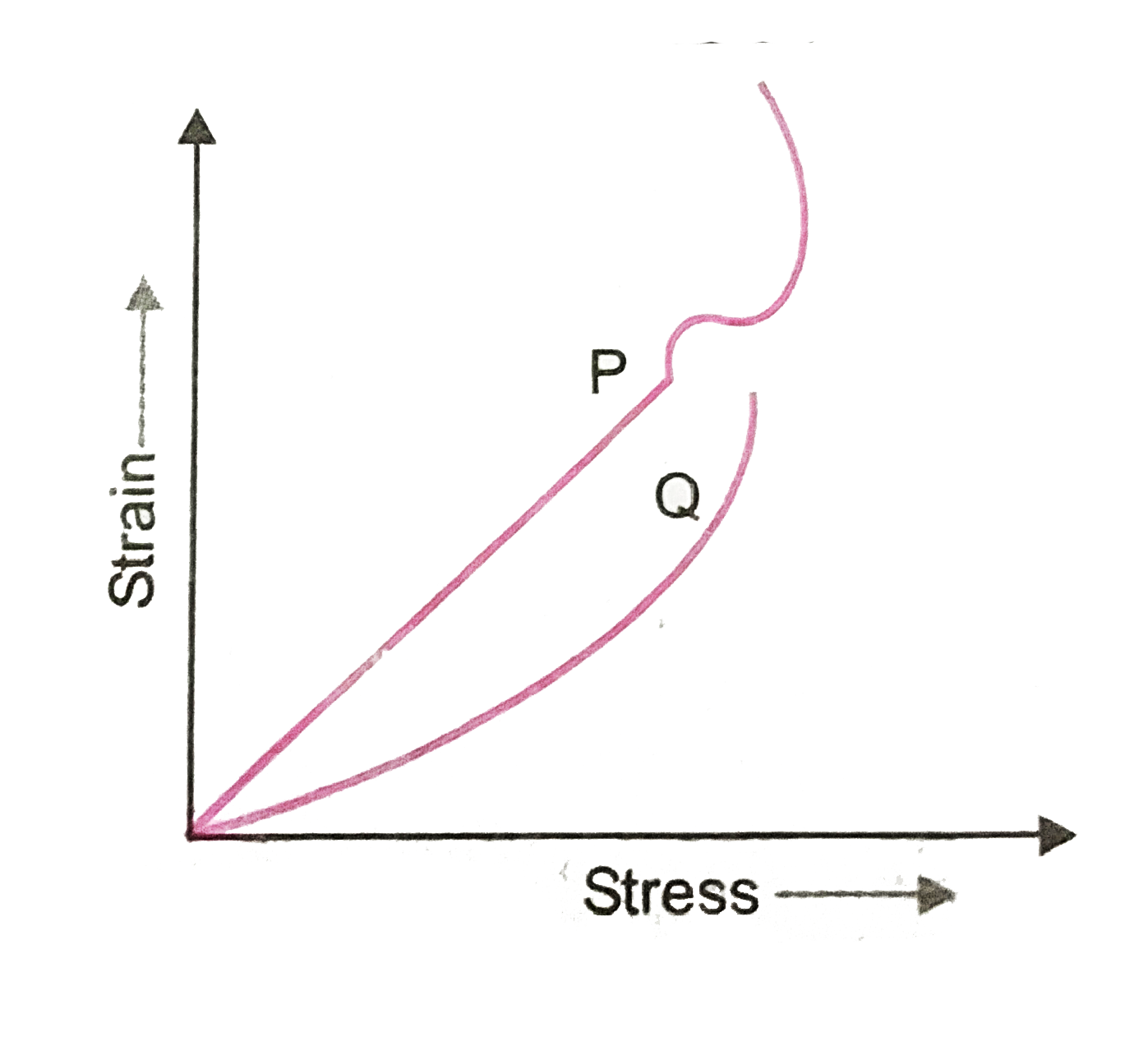
View SolutionA spherical body of radius R consists of a fluid of constant density and is in equilibrium under its own gravity. If P(r) is the pressure at r(rltR), then the correct option(s) is (are)
View SolutionTwo spheres P and Q of equal radii have densities `rho_1` and `rho_2`, respectively. The spheres are connected by a massless string and placed in liquids `L_1` and `L_2` of densities `sigma_1` and `sigma_2` and viscosities `eta_1` and `eta_2`, respectively. They float in equilibrium with the sphere P in `L_1` and sphere Q in `L_2` and the string being taut(see figure). If sphere P alone in `L_2` has terminal velocity `vecV_p` and Q alone in `L_1` has terminal velocity `vecV_Q`, then
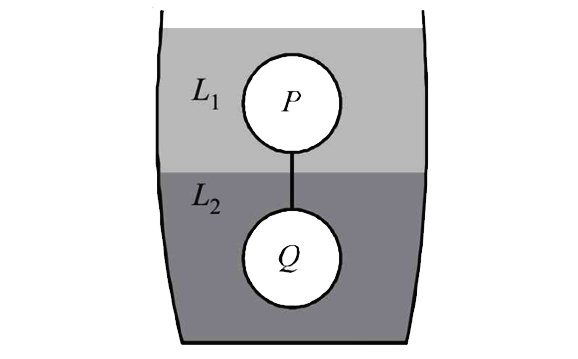
View SolutionA column of mercury of 10cm length is contained in the middle of a narrow horizontal 1m long tube which is closed at both the ends. Both the halves of the tube contain air at a pressure of 76 cm of mercury. By what distance will the column of mercury be displaced if the tube is held vertically?
View SolutionA point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View SolutionA cube of wood supporting 200gm mass just floats in water. When the mass is removed, the cube ruses by 2cm. What is the size of the cube?
View SolutionA boat floating in a water tank is carrying a number of large stones. If the stones are unloaded into water, what will happen to the water level?
View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle `theta` that the plank makes with the vertical in the equilibrium position. (Exclude the case `theta=theta^@`)

View SolutionA ball of density d is dropped on to a horizontal solid surface. It bounces elastically from the surface and returns to its original position in a time `t_1`. Next, the ball is released and it falls through the same height before striking the surface of a liquid of density of `d_L`
(a) If `dltd_L`, obtain an expression (in terms of d, `t_1` and `d_L`) for the time `t_2` the ball takes to come back to the position from which it was released.
(b) Is the motion of the ball simple harmonic?
(c) If `d=d_L`, how does the speed of the ball depend on its depth inside the liquid? Neglect all frictional and other dissipative forces. Assume the depth of the liquid to be large.
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_0`.
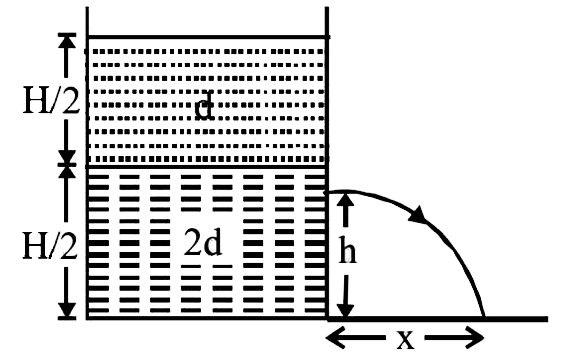
(a) A homogeneous solid cylinder of length `L(LltH//2)`, cross-sectional area `A//5` is immersed such that it floats with its axis vertical at the liquid-liquid interface with length `L//4` in the denser liquid. Determine:
(i) the density D of the solid and
(ii) the total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area `s(slt ltA)` is punched on the vertical side of the container at a height `h(hltH//2)`. Determine:
(i) the initial speed of efflux of the liquid at the hole,
(ii) the horizontal distance x travelled by the liquid initially, and
(iii) the height `h_m` at which the hole should be punched so that the liquid travels the maximum distance `x_m` initially. Also calculate `x_m`.
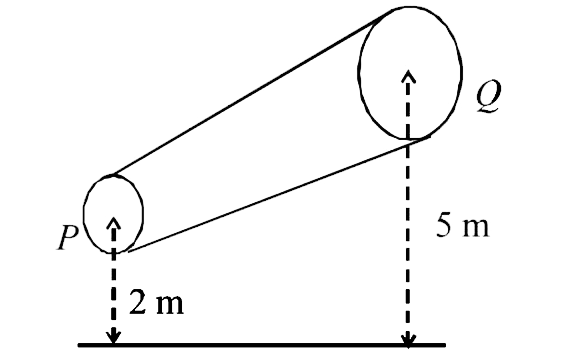
View SolutionA non-viscous liquid of constant density `1000kg//m^3` flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively `4xx10^-3m^2` and `8xx10^-3m^2`. The velocity of the liquid at point P is `1m//s`. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.
View SolutionA uniform solid cylinder of density `0.8g//cm^3` floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are `0.7g//cm^3` and `1.2g//cm^3`, respectively. The height of liquid A is `h_A=1.2cm.` The length of the part of the cylinder immersed in liquid B is `h_B=0.8cm`.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
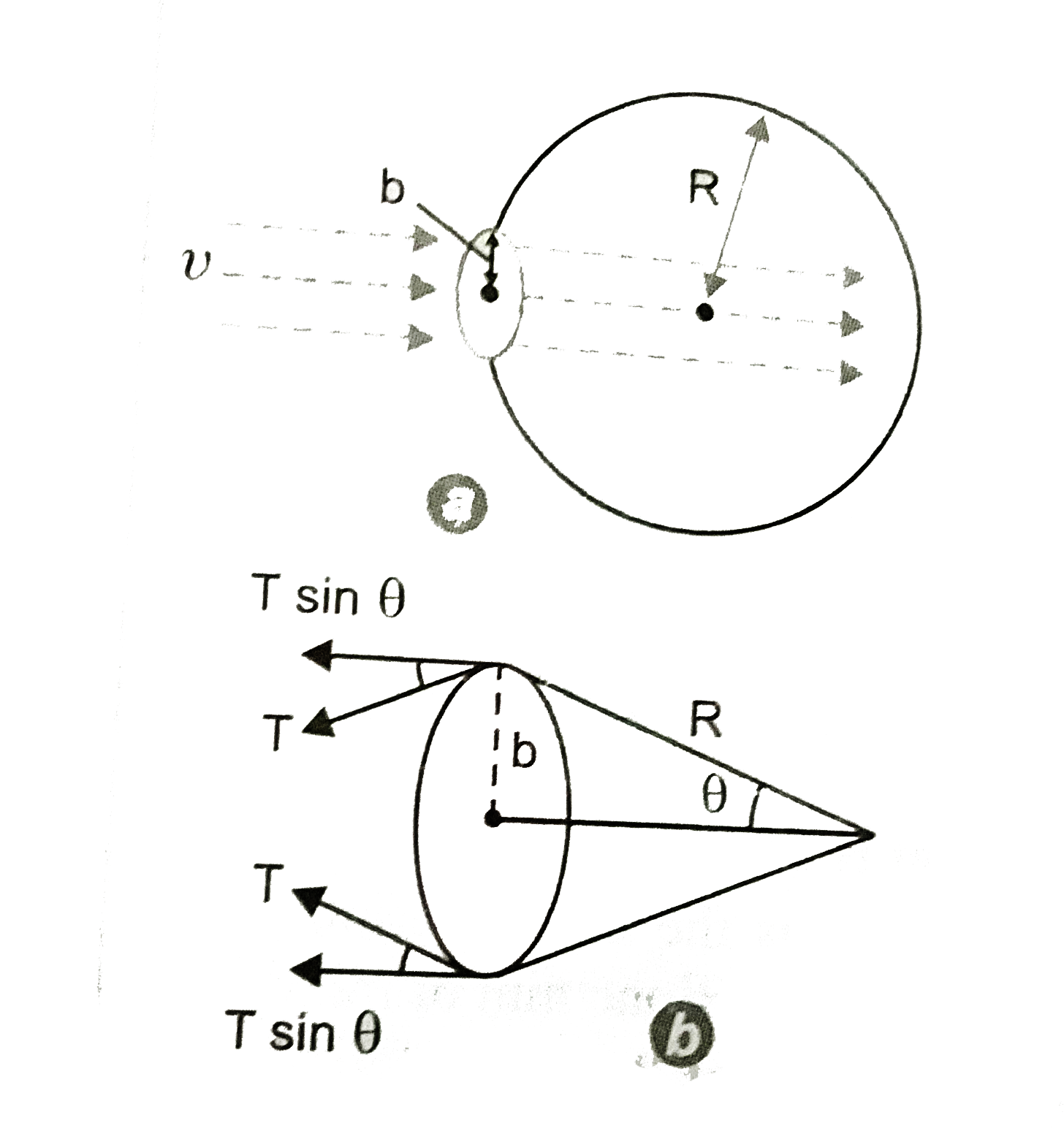
View SolutionA bubble having surface tension T and radius R is formed on a ring of radius b `(b lt gt R)` . Air is blown inside the tube held in front of the ring , with velocity `upsilon` as shown in fig. The air molecules collides perpendicularly with the wall of the bubble and stops. Calculate the radius R at which the bubble and stops. Calculate the radius R at which the bubble separates from the ring.
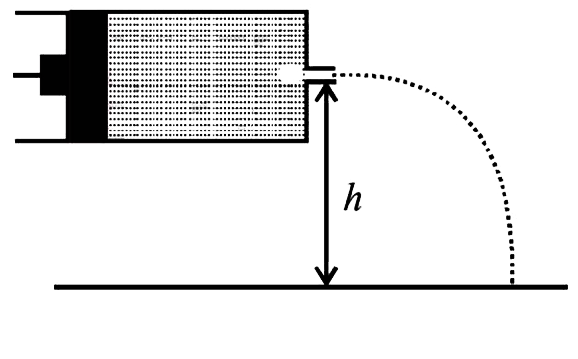
View SolutionA tube has two area of cross-section as shown in figure. The diameters of the tube are 8mm and 2mm. Find range of water falling on horizontal surface, if pistion is moving with a constant velocity of `0.25m//s`, `h=1.25m(g=10m//s^2)`
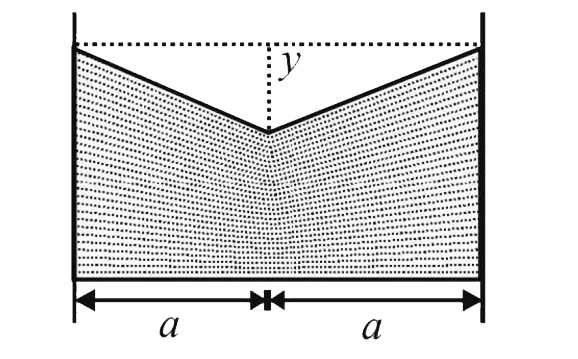
View SolutionA uniform wire having mass per unit length `lambda` is placed over a liquid surface. The wire causes the liquid to depress by `y(y lt lt a)` as shown in figure. Find surface tension of liquid. Neglect end effect.
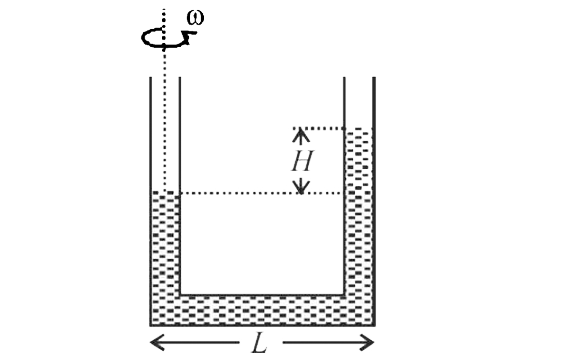
View SolutionA U tube is rotated about one of it's limbs with an angular velocity `omega`. Find the difference in height H of the liquid (density `rho`) level, where diameter of the tube `dlt lt L`.
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density `rho//3`.

Situation I: Initially, the tank is filled with water of density `rho` to a height such that the height of water above the top of the block is `h_1` (measured from the top of the block).
Situation II: The water is removed from the tank to a height `h_2` (measured from the bottom of the block), as shown in the figure. The height `h_2` is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height `h_1` (in situation 1), for which the block just starts to move up?
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density `rho//3`.

Situation I: Initially, the tank is filled with water of density `rho` to a height such that the height of water above the top of the block is `h_1` (measured from the top of the block).
Situation II: The water is removed from the tank to a height `h_2` (measured from the bottom of the block), as shown in the figure. The height `h_2` is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level `h_2` (in situation 2), for which the block remains in its origin) position whithout the application of any external force
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density `rho//3`.

Situation I: Initially, the tank is filled with water of density `rho` to a height such that the height of water above the top of the block is `h_1` (measured from the top of the block).
Situation II: The water is removed from the tank to a height `h_2` (measured from the bottom of the block), as shown in the figure. The height `h_2` is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
In situation 2, if `h_2` is further decreased, then
View SolutionWhen liquid medicine of density `rho` is to put in the eye, it is done with the help of a dropper. As the bulp on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
If the radius of the opening of the dropper is r, the vertical force due to the surface tension on the drop of radius R (assuming r ltltR) is
View SolutionWhen liquid medicine of density `rho` is to put in the eye, it is done with the help of a dropper. As the bulp on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
If `r=5xx10^-4m`, `rho=10^3 kgm^-3`, `g=10ms^-2`, `T=0.11Nm^-1`, the radius of the drop when it detaches from the dropper is approximately
View SolutionWhen liquid medicine of density `rho` is to put in the eye, it is done with the help of a dropper. As the bulp on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
After the drop detaches, its surface energy is
View SolutionA spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.

If the piston is pushed at a speed of `5mms^-1`, the air comes out of the nozzle with a speed of
View SolutionA spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.
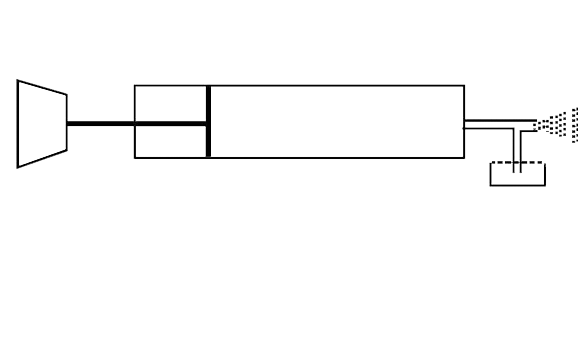
If the density of air is `rho_a`, and that of the liquid `rho_l`, then for a given piston speed the rate (volume per unit time) at which the liquid is sprayed will be proportional to
View SolutionSTATEMENT-1: The stream of water flowing at high speed from a garden hose pipe tends to spread like a fountain when held vertically up, but tends to narrow down when held vertically down.
STATEMENT-2: In any steady flow of an incompressible fluid, the volume flow rate of the fluid remains constant.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure `8N//m^2`.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is `0.04N//m`. Find tha ratio `n_B//n_A`, where `n_A` and `n_B` are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionA cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure `=1.0xx10^5N//m^2`, density of water=`1000kg//m^3` and `g=10m//s^2`. Neglect any effect of surface tension.]
View SolutionA `0.1kg` mass is suspended from a wire of negligible mass. The length of the wire is 1m and its crosssectional are is `4.9xx10^-7m^2`. If the mass is pulled a little in the vertically downward direction and released, it performs simple harmonic motion of angular frequency `140 rad s^-1`. If the Young's modulus of the material of the wire is `nxx10^9 Nm^-2`, the value of n is
View SolutionConsider two solid spheres P and Q each of density `8gm cm^-3` and diameters 1cm and 0.5cm, respectively. Sphere P is dropped into a liquid of density `0.8gm cm^-3` and viscosity `eta=3` poiseulles. Sphere Q is dropped into a liquid of density `1.6gmcm^-3` and viscosity `eta=2` poiseulles. The ratio of the terminal velocities of P and Q is
View SolutionA spring of force constant `800N//m` has an extension of 5cm. The work done in extending it from 5cm to 15cm is
View SolutionA wire fixed at the upper end stretches by length l by applying a force F. The work done in stretching is
View SolutionSpherical balls of radius 'R' are falling in a viscous fluid of viscosity `'eta'` with a velocity 'v'. The retarding viscous force acting on the spherical ball is
View SolutionIf two soap bubbles of different radii are connected by a tube.
View SolutionIf 'S' is stress and 'Y' is young's modulus of material of a wire, the energy stored in the wire per unit volume is
View SolutionA 20cm long capillary tube is dipped in water. The water rises up to 8cm. If the entire arrangement is put in a freely falling elevator the length of water column in the capillary tube will be
View SolutionA wire elongates by l mm when a load W is hanged from it. If the wire goes over a pulley and two weights W each are hung at the two ends, the elongation of the wire will be (in mm)
View SolutionIf the terminal speed of a sphere of gold (density `=19.5kg//m^3`) is `0.2m//s` in a viscous liquid (density `=1.5kg//m^3`), find the terminal speed of a sphere of silver (density `=10.5kg//m^3`) of the same size in the same liquid
View SolutionA spherical solid ball of volume V is made of a material of density `rho_1`. It is falling through a liquid of density `rho_2(rho_2ltrho_1)`. Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed v, i.e., `F_(viscous)=-kv^2(kgt0)`. The terminal speed of the ball is
View SolutionA jar is filled with two non-mixing liquids 1 and 2 haivng densities `rho_1` and `rho_2` respectively. A solid ball, made of a material of density `rho_3` , is dropped in the jar. It comes to equilibrium in the position shown in the figure. Which of the following is true for `rho_1`, `rho_1` and `rho_3`?

View SolutionA capillary tube (A) is dipped in water. Another identical tube (B) is dipped in a soap-water solution. Which of the following shows the relative nature of the liquid columns in the two tubes?
View SolutionTwo wires are made of the same material and have the same volume. However wire 1 has cross-sectional area A and wire 2 has cross-sectional area 3A. If the length of wire 1 increases by `Deltax` on applying force F, how much force is needed to stretch wire 2 by the same amount?
View SolutionA ball is made of a material of density `rho` where `rho_(oil)ltrholtrho_(water)` with `rho_(oil)` and `rho_(water)` representing the densities of oil and water, respectively. The oil and water are immiscible. If the above ball is in equilibrium in a mixture of this oil and water, which of the following pictures represents its equilibrium position?
View SolutionTwo identical charged spheres are suspended by strings of equal lengths. The strings make an angle of `30^@` with each other. When suspended in a liquid of density `0.8gcm^-3`, the angle remains the same. If density of the material of the sphere is `1.6gcm^-3`, the dielectric constant of the liquid is
View SolutionWork done in increasing the size of a soap bubble from a radius of 3cm to 5cm is nearly (Surface tension of soap solution `=0.03Nm^-1`)
View SolutionWater is flowing continuously from a tap having an internal diameter `8xx10^-3m`. The water velocity as it leaves the tap is `0.4ms^-1`. The diameter of the water stream at a distance `2xx10^-1m` below the tap is close to:
View SolutionA thin liquid film formed between a U-shaped wire and a light slider supports a weight of `1.5xx10^-2N` (see figure). The length of the slider is 30cm and its weight negligible. The surface tension of the liquid film is

View SolutionA uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring such that it is half submerged in a liquid of density `sigma` at equilibrium position. The extension `x_0` of the spring when it is in equlibrium is:
View SolutionAssume that a drop of liquid evaporates by decreases in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible? The surface tension is T, density of liquid is `rho` and L is its latent heat of vaporization.
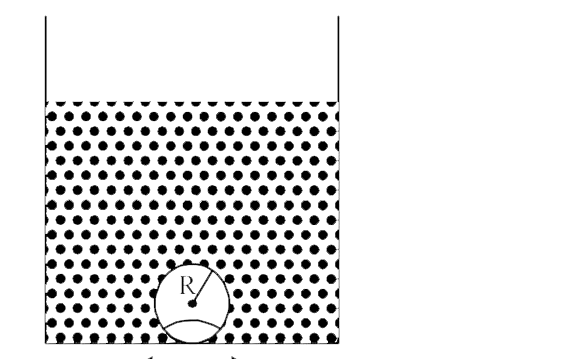
View SolutionOn heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If `rlt ltR` and the surface tension of water is T, value of r just before bubbles detach is: (density of water is `rho_w`)
View SolutionAn open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)
View Solution
JEE Main And Advanced questions and complete solutions for chapter MECHANICAL PROPERTIES OF MATTER AND FLUIDS of SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) of Class 11