Complete Solutions to JEE Main And Advanced of chapter ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| SUNIL BATRA | JEE Main And Advanced |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height `3a/4` above the base. The minimum value of F which the cube begins to tip about the edge is ....(Assume that the cube does not slide).
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beada are at the centre of the rod and the system is rotating with an angular velocity `omega_0` about an axis perpenducular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View SolutionA cylinder of mass M and radius R is resting on a horizontal paltform (which is parallel to the x-y plane) with its exis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by `x =A cos (omega t).` There is no slipping between the cylinder and platform. The maximum torque acitng on the cylinder during its motion is ..................
View SolutionA stone of mass m tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by `T = Ar^2` where A is a constant, r is the instantaneous radius fo the circle and n=....
View SolutionA rod of weight `w` is supported by two parallel knife edges `A` and `B` and is in equilibrium in a horizontal position. The knives are at a distance `d` from each other. The centre of mass of the rod is at a distance `x` from `A`.
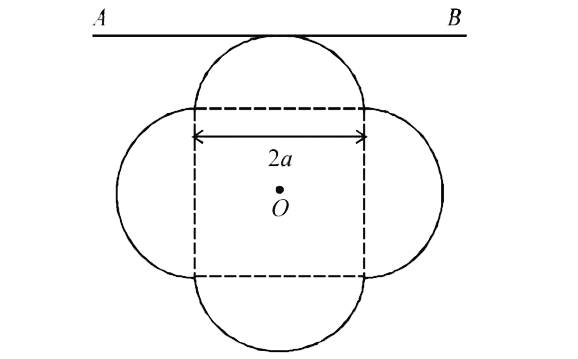
View SolutionA symmetric lamina of mass M consists of a square shape with a semicircular section over of the edge of the square as shown in fig. p-10. The side of the square is 2a. The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is `1.6Ma^2`. The moment of inertia of the lamina is ......
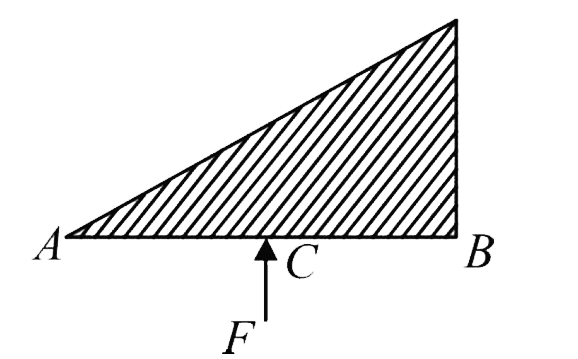
View SolutionA triangular plate of uniform thickness and density is made to rotate about an axis perpendicular to the plane of the paper and (a) passing through A,(b) passing through B, by the application of the same force, F, at C (midpoint of AB) as shown in the figure. The angular acceleration in both the cases will be the same.
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity `omega.` another disc of the same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is `2 omega //sqrt5.`
View SolutionA ring of mass 0.3 kg and radius 0.1 m and a solid cylinder of mass 0.4 kg and of the same radius are given the same kinetic energy and released simultaneously on a flat horizontal towards a wall which is at the same distance from the ring and the cylinder. The rolling friction in both cases is negligible. The cylinder will reach the wall first.
View SolutionTwo particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m//s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity `omega`, Two objects, each of mass m, are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity.
View SolutionTwo point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
View SolutionA smooth sphere A is moving on a frictionless horizontal plane with angular speed `omega` and centre of mass velocity `upsilon`. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are `omega_A and omega_B` respectively. Then
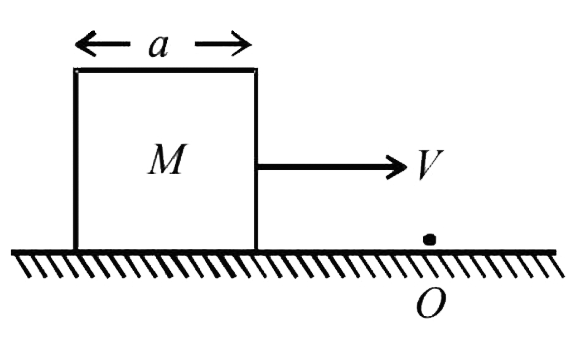
View SolutionA cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in Figure. It hits a ridge at point O. The angular speed fo the block after it hits O is
View SolutionA long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration `alpha.` if the coefficient of friction between the rod and the bead is `mu`, and gravity is neglected, then the time after which the bead starts slipping is
View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction `mu`. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

View SolutionA thin wire of length L and uniform linear mass density `rho` is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX is
`
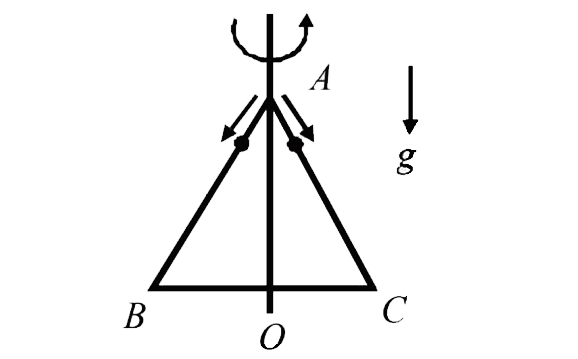
View SolutionAn equailaral triangle ABC formed from a uniform wire has two small identical beads initially located at A. The triangle is set rotating about the vertical axis AO. Then the beads are released from rest simultaneously and allowed to slide down, one along AB and the other along AC as shown. Neglectig frictional effects, the equatities that are conserved as the beads slids down, are
View SolutionOne quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. it is made to rotate about a line perpendicular to its plane and passing through the center of the original disc. Its moment of inertia about the axis of rotation is
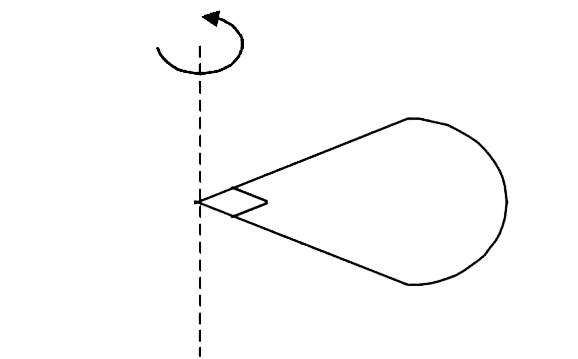
View SolutionA cylinder rolls up an inclined plane, reaches some height, and then rolls down (without slipping throughout these motions). The directions of the frictional force acting on the cylinder are.
View SolutionA circular plarform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity `omega_0`. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform `omega(t)` will vary with time t as
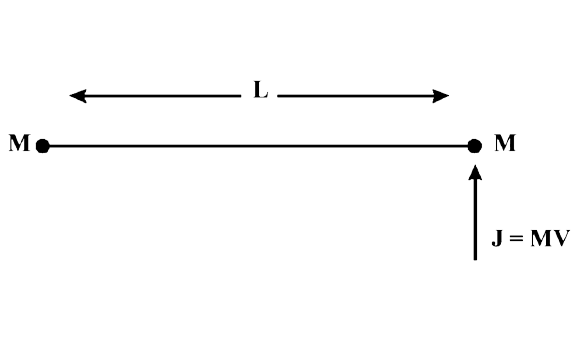
View SolutionConsider a body, shown in figure, consisting of two identical balls, each of mass M connected by a light rigid rod. If an impulse J = MV is imparted to the body at one of its ends what would be it angular velocity?
View SolutionA particle undergoes uniform circular motion. About which point on the plane of the circle, will the angular momentum of the particle remain conserved?
View SolutionA horizontal circular plate is rotating about a vertical exis passing through its centre with an angular velocity `omega_0`. A man sitting at the centre having two blocks in his hands stretches out his hands so that the moment of inertia of the system doubles. if the kinetic energy oif the system is K initially, its final kinetic energy will be
View SolutionA disc is rolling without slipping with angular velocity `omega`. P and Q are two points equidistant from the centre C. the order of magnitude fo velocity is

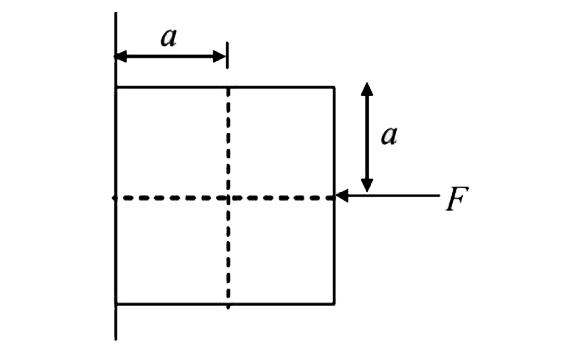
View SolutionA block of mass m is at rest under the action of force F against a wall as shown in figure. Which of the following statement is incorrect?
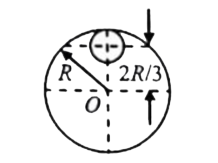
View SolutionA thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
View SolutionA particle is confined to rotate in a circular path decreasing linear speed, then which of the following is correct?
View SolutionA solid sphere of mass M and radius R having moment of inertia I about its diameter is recast into a solid disc abut an axis passing the edge and perpendicular to the plane remains l. Then R and r are related as
View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v. it reaches up to a maximum height of `(3v^2)/(4g)
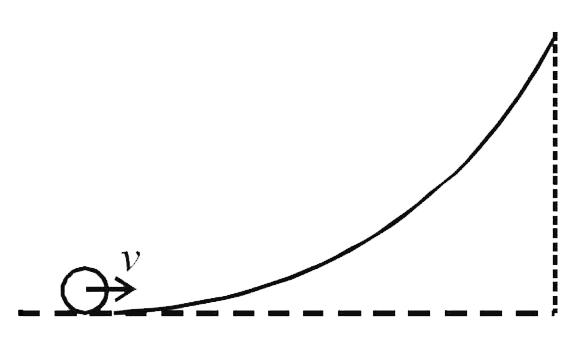
with respect to the initial position. The object is
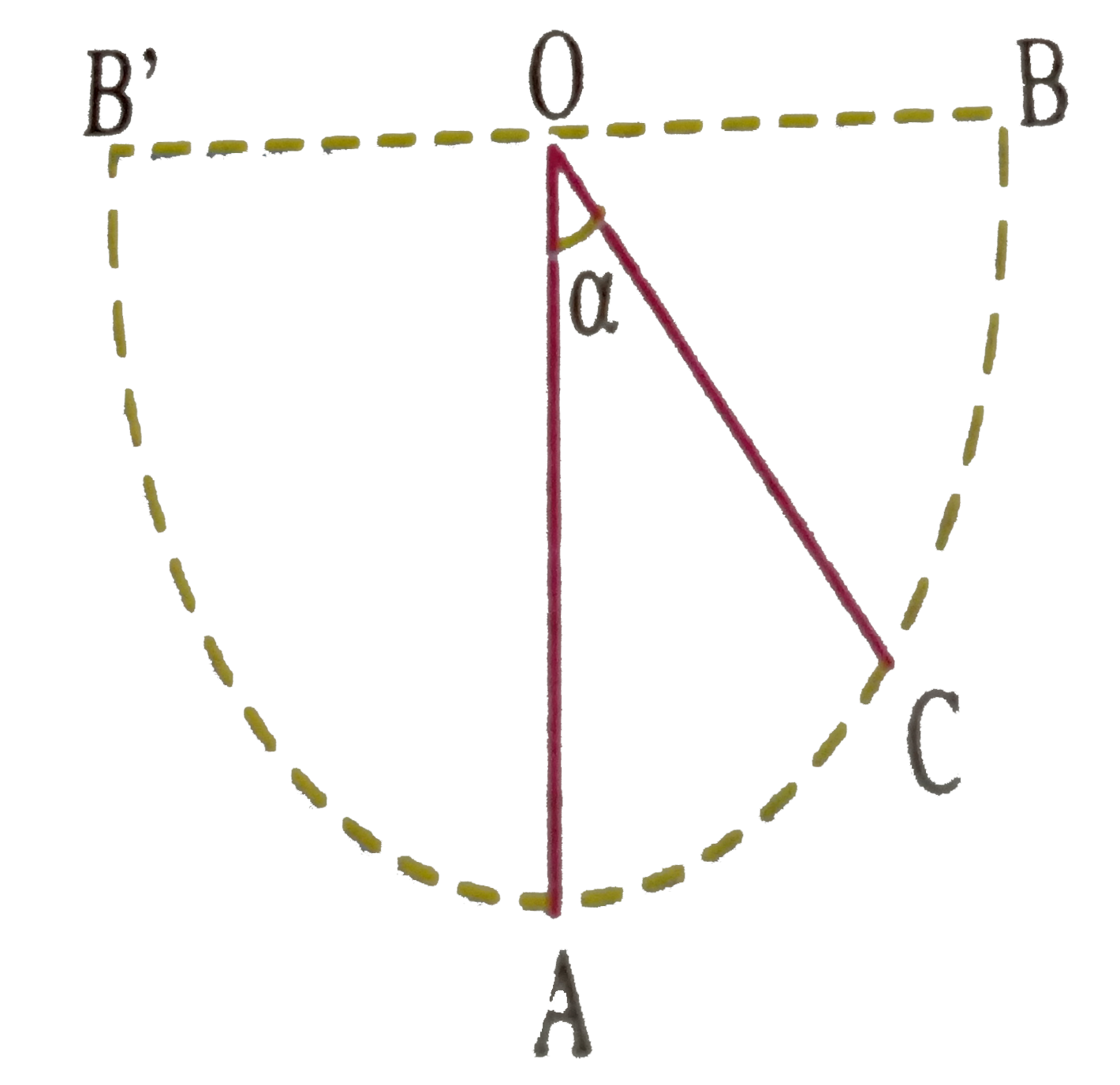
View SolutionA bob of mas `M` is suspended by a massless string of length `L`. The horizontal velocity `v` at position `A` is just sufficient to make it reach the point `B`. The angle `theta` at which the speed of the bob is half of that at `A`, satisfies.
 .
.
View SolutionLook at the drawing given in the figure which has been drawn with ink of uniform line-thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is m. The mass of the ink used to draw the outer circle is 6 m. The coordinates of the centres of the different parts are: outer cicle (0,0), left circle (-a, a), right inner circle (a,a), vertical line (0,0) and horizontal line (0 ,-a). The y-coordinate of the centre of mass of the ink in this drawing is

View SolutionA small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the x-y plane with centre at O and constant angular speed `omega`. If the angular momentum of the system. calculated about O and P are denoted. by `vacL_O and vac_P` respectively, then.

View SolutionA thin uniform rod, pivoted at O, is rotating in the horizontal plane with constatn angular speed `omega`, as shown in the figure. At time t = 0, a small insect starts from O and moves with constant sped v, with respect to the rod towards the other end. It reaches the end of the rod at t =T and stops. The angular speed of the system remains `omega` throughout. The magnitude of the torque `(|vecpi|)` about O, as a function of time is best represented by which plot?
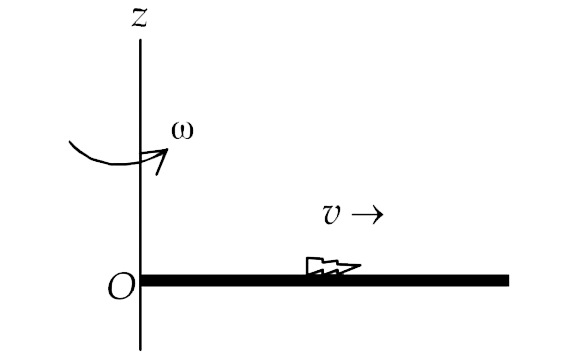
View SolutionA uniform wooden stick of mass 1.6 kg and length l rests in an inclined mannar on a smooth, vertical wall of height `h(ltl)` such that a small portion of the stick extends beyond the wall. The reaction force of th wall on the stick is perpendicular to the stick. The stick makes an angle of `30^@` with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio h/l and the friectional force f at the bottom of the stick are `(g = 10 ms^2)`
View SolutionTwo particles `A` and `B` initially at rest, move towards each other, under mutual force of attraction. At an instance when the speed of `A` is `v` and speed of `B` is `2v`, the speed of centre of mass (`CM`) is
View SolutionA mass M moving with a constant velocity parlale to the X-axis. Its angular momentum with respect to the origin
View SolutionWhen a bicycle is motion the force of friction exerted by the ground on the two wheels is such that is acts .
View SolutionA particle of mass m is projected with a velocity v making an angle of `45^@` with the horizontal. The magnitude of the angular momentum of the projectile abut the point of projection when the particle is at its maximum height h is.
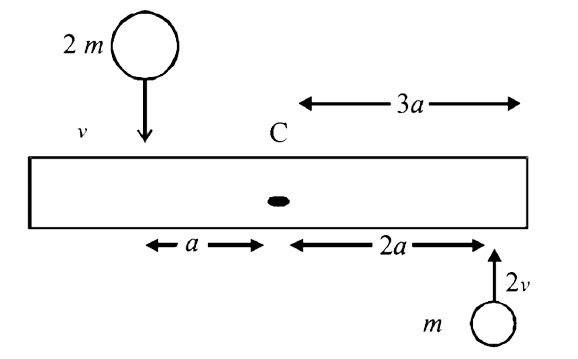
View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar [as shown in the fig.] and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by `omega`, E and `v_c` respecitvely, we have after collison
View SolutionThe moment of inertia of a thin square plate ABCD, fig, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
where `l_1, l_2, l_3 and l_4` are respectively the moments of intertial about axis 1,2,3 and 4 which are in the plane of the plate.
View SolutionA tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity `omega`. Determine the force exerted by the liquid at the other end.
View SolutionA car is moving in a circular horizonta track of radius 10m with a constant speed of 10 m/s. A pendulum bob is suspended from the roof of the cat by a light rigid rod of length 1.00m. The angle made by the rod with track is
View SolutionLet `I` be the moment of interia of a uniform square plate about an axis `AB` that passses through its centre and is parallel to two its sides. `CD` is a line in the plane of the plate that passes through the centre of the plate and makes an angle `theta` with `AB`. The moment of inertia of the plate about the axis `CD` is then equal to-
View SolutionThe torque `tau` on a body about a given point is found to be equal to A x L, where A is constant vector and L is the angular momentum of the body that point. From this, it follows that
View SolutionA solid cylinder is rolling down a rough inclined plane of inclination `theta`. Then
View SolutionIf the resultant of all the external forces acting on a system of particles is zero. Then from an inertial frame, one can surely say that
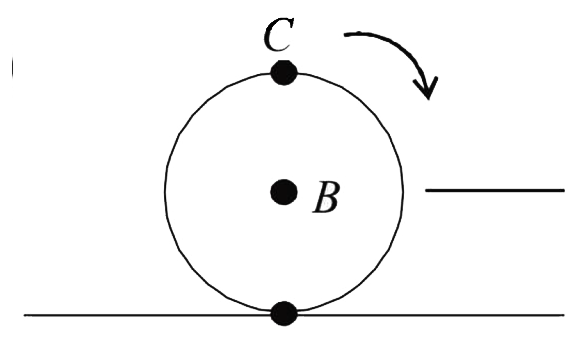
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
View SolutionTwo solid spheres A and B of equal volumes but of different densities `d_A and d_B` are connected by a string. They are fully immersed in a fluid of density `d_F`. They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if

View SolutionA thin ring of mass 2kg and radius 0.5 m is rolling without slipping on a horizontal plane with velocity 1m/s. A small ball of mass 0.1kg, moving with velocity 20 m/s in the opposite direction hits the ring at a height of 0.75m and goes vertically up with velocity 10m/s. Immediately after the collision

View SolutionThe figure shows a system consisting of (i) a ring the outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed `omega` and (ii) an inner disc of radius 2R rotating anti clockwise with angular speed `omega//2.` The ring and disc are separated. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of `30^@` with the horizontal. Then with respect to the horizontal surface,
View SolutionTwo solid cylinders P and Q of same mass and same radius start rolling down a fixed inclined plane from the same height at the same time. Cylinder P has most of its mass concentrated near its surface, while Q has most its mass concentrated near the axis. Which statement(s) is (are) correct?
View SolutionIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle `theta` with the horizontal floor. The coefficient of friction between the wall and the ladder is `mu_1` and that between the floor and the ladder is `mu_2.` the normal reaction of the wall on the ladder is `N_1` and that of the floor is `N_2.` if the ladder is about to slip. than

View SolutionA ring of mass M and radius R is rotating with angular speed `omega` about a fixed vertical axis passing through its centre O with two point masses each of mass `(M)/(8)` at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is `(8)/(9) omega` and one fo the masses is at a distance of `(3)/(5) R` from O. At this instant the distance of the other mass from O is
View SolutionTwo thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a massless, rigid rod of length `l= sqrt(24a)` through their centres. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is `omega.` The angular momentum of the entire assembly about the point 'O' is `vecL` (see the figure). Which of the following statement (s) is (are) true?

View SolutionThe position vector `vacr` of the z-component of `vecL` is `55ma^2omega`. Following equation
`vacr(t)= alphat^3hati+beta^2hatj,`
where `alpha = 10//3ms^(-3), beta = 5 ms^(-2)` and m = 0.1kg. At t=1s, which of the following statement (s) is (are) true about the particle?
View SolutionA 40 kg mass, hanging at the end fo a rope of length l, oscillates in a vertical plane with an angular amplitude `theta_0.` What is the tension in the rope when it makes en angle `theta` with the vertical ? If the breaking strength of the rope is 80kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?
View SolutionA large mass M and a small mass m hang at two ends of a string that passes over a smooth tube as shown in the figure. The mass m moves around a circular path which lies in a horizontal plane. The length of string from the mass m to the top of the tube is l and `theta` is the 'angle' this length makes with the vertical. What should be the frequency of rotation of mass m, so that the mass M remains stationary?

View SolutionA circular plate of unifrom thickness has a diameter of `56 cm`. A circular portion of diameter `42 cm` is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View SolutionA block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?

View SolutionA particle is projected at time t=0 from a point P on the ground with a speed `v_0,` at an angle of `45^@` to the horizontal. Find the magnitude and direction of the angular momentum of the particle about P at tiem `t= v_0//g`
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part, The horizontal part, is 1.0 metre above the ground lenvel and the top of the track is 2.4 meters above the ground. Find the distance on the ground with respect to the point B (which is vertically below the end of the track as shown i fig.) where the sphere lands. During its flight as a projectlie, does the sphere continue to rotate about its centre of mass? Explain.

View SolutionA thin uniform bar lies on a frictionless horizonta surface and is free to move in any way on th surface. Its mass is 0.16 kg and length `sqrt3`meters. Two particless, each of mass 0.08 kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10 m/s, and other with 6m/s as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distane of 0.5m from the centre of the bar. The particles strike the bar at the same instant of time and stick to the bar on collision. Calculate the loss of the kinetic energy of the system in the above collision process.
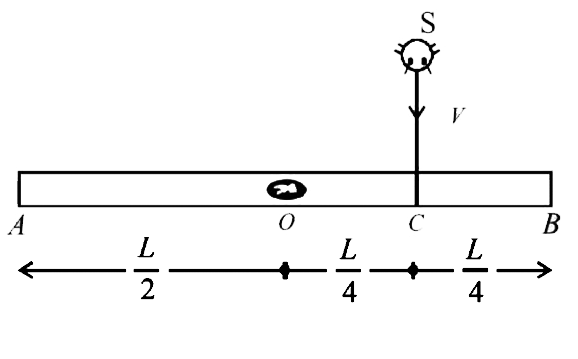
View SolutionA homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity `omega` in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of `90^@`, determine V.

View SolutionA uniform thin rod of mass m and length L is standing vertically along the y-axis on a smooth horizontal surface, with its lower end at the origin (0,0). A slight disturbane at t = 0 causes the lower end t slip on the smooth surface along the positive x-axis, and the rod starts falling.
(i) What is the path followed by the centr of mass of the rod during its fall?
(ii) Find the equaiton to the trajectory of a point on the rod shape of the path of this point?
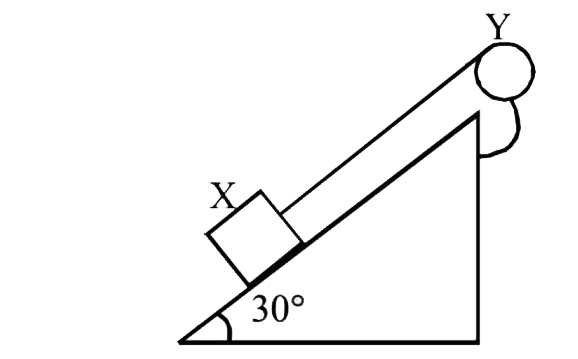
View SolutionA block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination `30^@` to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2kg and of radius 0.2 and of radius 0.2 m as shown in Fingure. The drum is given an initial angular velocity such that the block X starts moving up the plane.
(i) Find the tension in the string during the motion.
(ii) At a certain instant of time the magnitude of the angular velocity of Y s `10 rad s^(-1)` calculate the distance travelled by X from that instant of time until it comes to rest
View SolutionTwo uniform thin rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02kg respectively are rigidly joined end to end. The combination is pivoted at the lighter end, P as shown in fig. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05kg, moving horizontally, hits the lower end of the combination and sticks to it what should be the velocity of the object so that the system could just be reised to the horizontal position.
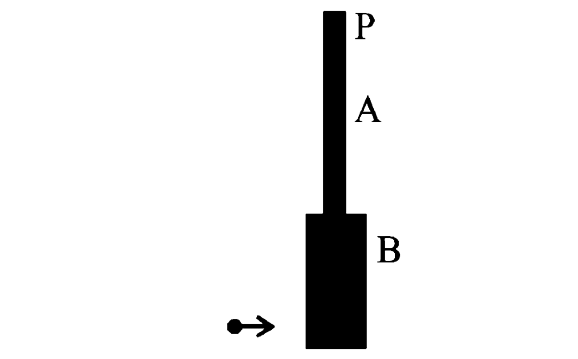
View SolutionA rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radus R is placed horizontally at rest its length parallel to the edge such that the exis of the cylinder and the endg of the block are in the same vertical plane as shown in the figure below. Ther is sufficinet friction present at the edge s that a very small displacement causes the cylinder to roll off the edge without slipping. Determine:

(a) the angle `theta_c` through which the cylinder rotates before it leaves contact with the edge,
(b) the speed of the centre of mass of the cylinder before leaving contact with the edge, and
(c) the ratio of the translational to rotational kinetic energy of the cylinder when its centre of mass is in horizontal line with the edge.
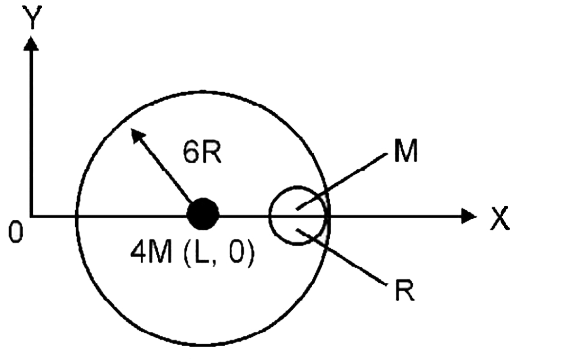
View SolutionA small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively , this arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
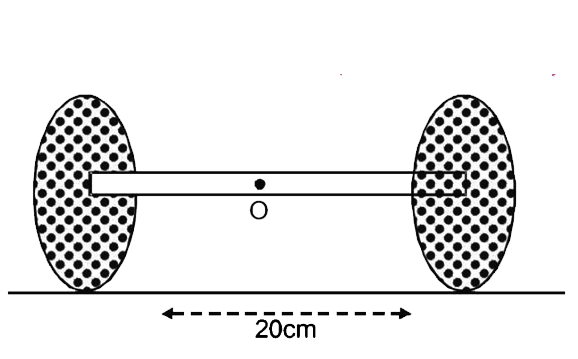
View SolutionTwo thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of `9m//s^2` Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors `hati, hatj and hatk` in the x,y, and z directions.
View SolutionA wedge of mass m and triangular cross- section (AB = BC = CA = 2R) is moving with a constant velocity `-v hat`I towards a sphere of radius R fixed on a smooth horizontal table as shown in figure. The wadge makes an elastic collision with the fixed sphere and returns along the same path without any rotaion. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very shot time. `Deltat,` during which the sphere exerts a constant force F on the wedge.
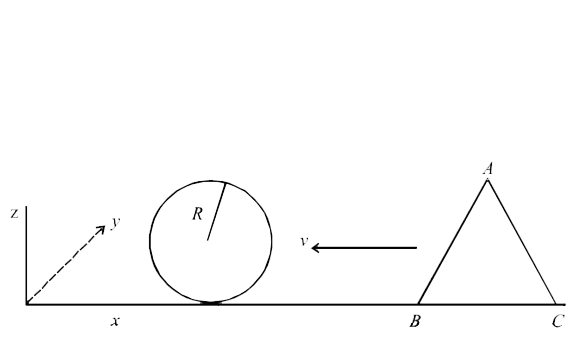
(a) Find the force F and also the normal force N exerted by the table on the wedge during the time `Deltat.`
(b) Ler h denote the perpendicular distance between the centre of mass of the wedge and the line of action of F. Find the magnitude of the torque due to the normal force N about the centre of the wedge, during the interval `Deltat.`
View SolutionA uniform circula disc has radius R and mass m. A particle also of mass m, is fixed at a point A on the edge of the disc as shown in figure. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially, the disc is held vertical with the point A at its highes position.
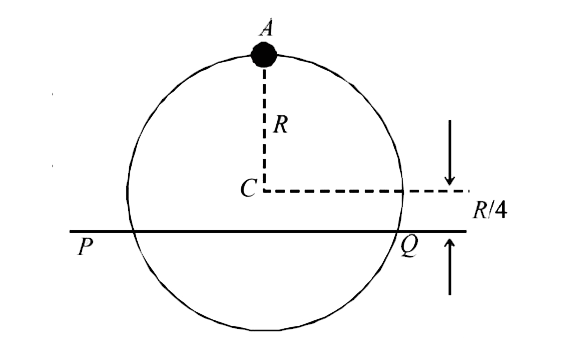
View SolutionA man pushes a cylinder of mass `m_1` with the help of a plank of mass `m_2` as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
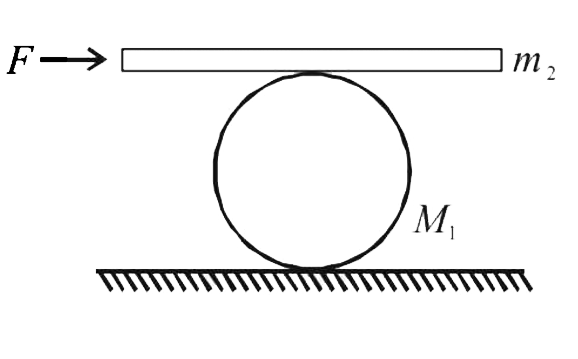
(b) the magnitudes and direction of frictional force at contact points.
View SolutionTwo heavy metallic plates are joined together at `90^@` to each other. A laminar sheet of mass 30kg is hinged at the line AB joining the two heavy metallic plates. The hinges are frictionless. The moment of inertia of the laminar sheet about an axis parallel to AB and passing through its center of mass is 1.2 kg `m^2.` Two rubber obstacles P and Q are fixed, one on each metallic plate at a distance 0.5m from the line AB. This distance is chosen so that the reaction due to the hinges on the laminar sheet is zero during the impact. Initially the laminar sheet hits one of the obstacles with an angular velocity 1 rad/s and turns back. If the impulse on the sheet due to each obstacle is 6 N-s,
(a) Find the location of the center of mass of the laminar sheet from AB.
(b) At what angular velocity does the laminar sheet come back after the first impact?
(c) After how many impacts, does the laminar sheet come to rest?
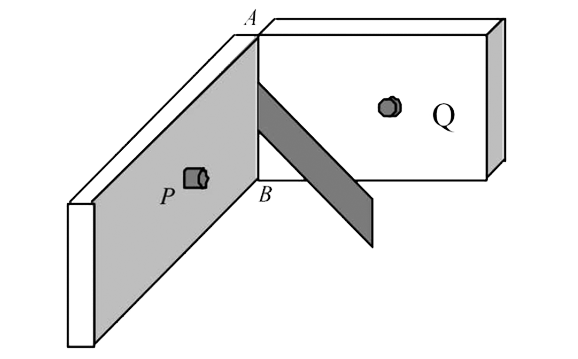
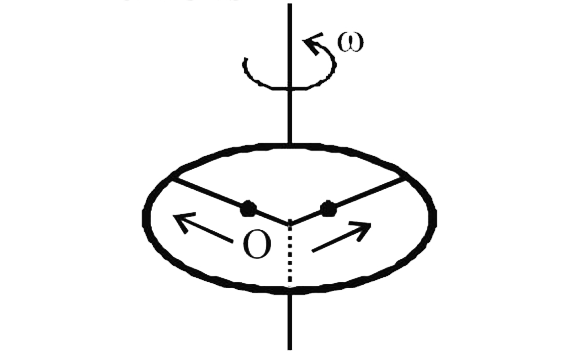
View SolutionThree particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizonta frictionsess table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity `omega`.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.

View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination `theta`. Calculate the linear acceleration of the axis of cylinder.
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
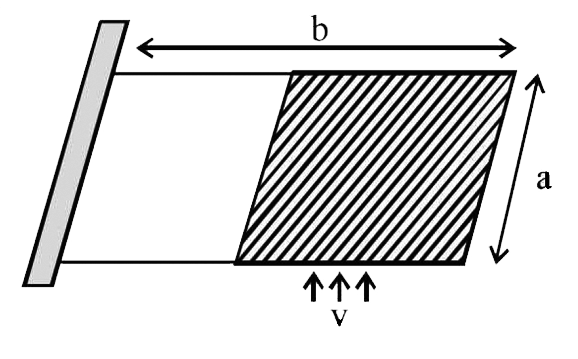
View SolutionA rectangular plate of mass M and dimension `axxb` is held in horizontal position by striking n small balls (each of mass m) per unit area per second. The balls are striking in the shaded half region of the plate. The collision of the balls with the plate is elastic. What is v? (Given n=100, `M =3 kg, m=0.01 kg, b = 2m, a =1m, g = 10m/s^2`).

View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity `2 omega` using the entire potential energy of a spring compressed by a distance `x_1` Disc B is imparted an angular velocity `omega` by a spring having the same spring constant and compressed by a distance `x_2` Both the discs rotate in the clockwise direction.
The ratio `x_1//x_2` is
View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity `2 omega` using the entire potential energy of a spring compressed by a distance `x_1` Disc B is imparted an angular velocity `omega` by a spring having the same spring constant and compressed by a distance `x_2` Both the discs rotate in the clockwise direction.
When disc B is brought in contact with disc A, they acquire a common angular velocity in time t. The average frictional torque on one disc by the other during this period is
View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity `2 omega` using the entire potential energy of a spring compressed by a distance `x_1` Disc B is imparted an angular velocity `omega` by a spring having the same spring constant and compressed by a distance `x_2` Both the discs rotate in the clockwise direction.
The loss of kinetic energy in the above process is
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity `vecV_0 = vacV_0hati.` The coefficinet of friction is `mu.`
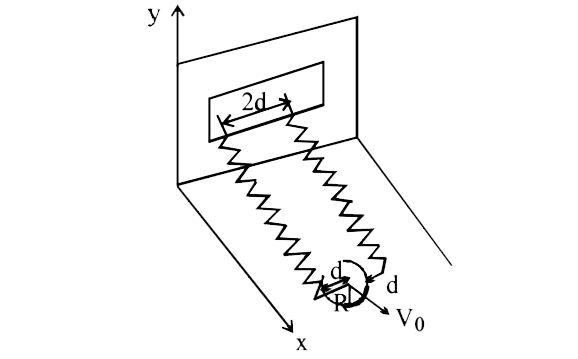
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity `vecV_0 = vacV_0hati.` The coefficinet of friction is `mu.`
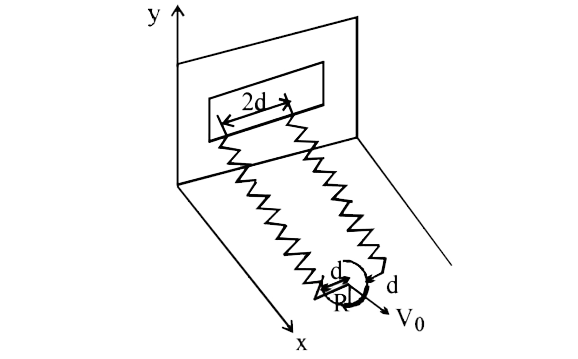
The centre of mass of the disk undergoes simple harmonic motion with angular frequency `omega` equal to -
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity `vecV_0 = vacV_0hati.` The coefficinet of friction is `mu.`

The maximum value of `V_0` for whic the disk will roll without slipping is-
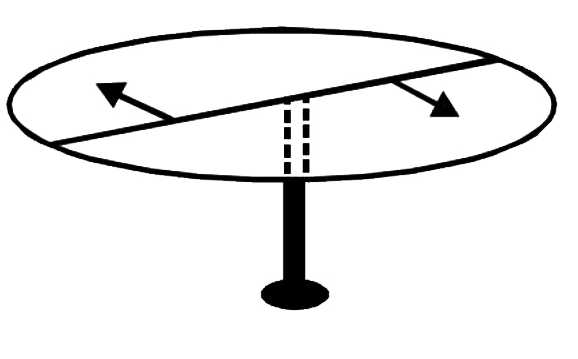
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed `omega` the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed `omega` in this case

Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of `45^@` with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed `omega` about the z-axis.
 .`
.`
Which of the following statements about the instantaneous axis (passing through the centre of mass) is correct?
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed `omega` the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed `omega` in this case
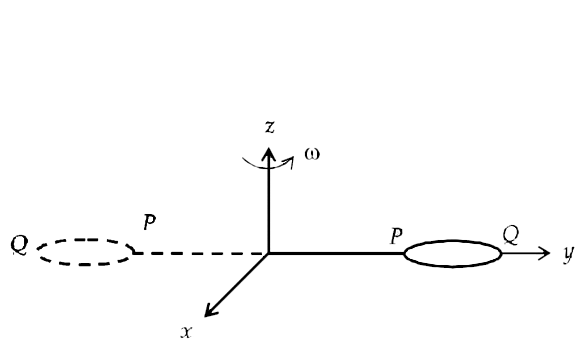
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of `45^@` with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed `omega` about the z-axis.
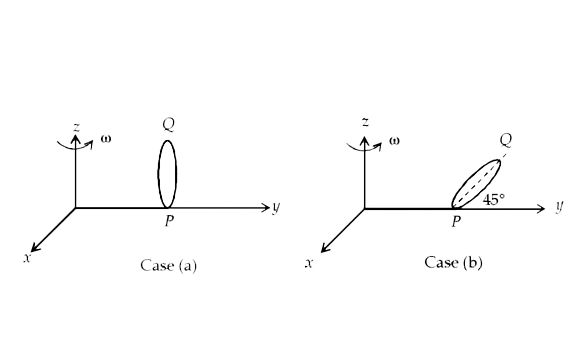
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
View SolutionSatement-1: if there is no external torque on a body about its centre of mass, then the velocity of the center of mass remains constant.
Statement-2: The linear momentum of an isolated system remains constant.
View SolutionSatement-1: two cylinder one hollow (metal) and the other side (wood) with the same mass and identical dimensions are simultaneously allowed to roll wihtout slipping down an inclined plane from the same height. The hollow cylinder will reach the bottom of the inclined plane first.
Statement-2: By the principle of conservation of energy, the total kinetic energies of both the cylinder are identical when they reach the bottom of the incline.
View SolutionA binary star consists of two stars `A(mass 2.2 M_s)` and B `(mass 11 M_s)` where `M_s` is the mass of the sun, they are separted by distane d and are rotating about their center of mass, which is stationary. The ratio of the total angular momentum of the binary to the angular momentum of star B about the centre of mass is
View SolutionA boy is pushing a ring of mass 2kg and radius 0.5 m with a stick as shown in figure. The stick applies a force of 2N on the ring and rolls it without slipping with an acceleration of `0.3 m/s^2.` The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring of (P/10). The value of P is

View SolutionFour solid spheres each of diameter `sqart5`cm and mass 0.5 kg are placed with their centers at the corners of a square of side 4cm. The moment is `Nxx10^(-4)kg - m^2` , then N is .
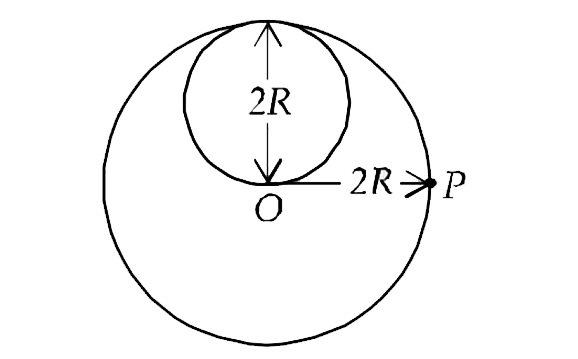
View SolutionA lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is `I_O and I_P` respectively. Both these axes are perpendiucalr to the plane of the lamina. The ratio `I_P/I_O` ot the nearest integer is
View SolutionA uniform circular disc of mass 50kg and radius 0.4 m is rotating with an angular velocity of `10 rad s^(-1)` about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity `(in red s^(-1))` of the system is
View SolutionA horizontal circular platform of radius 0.5 m and mass axis. Two massless spring toy-guns, each carrying a steel ball of mass 0.05 kg are attached to the platform at a distance 0.25m from the centre on its either sides along its diameter (see figure). Each gun simultaneously fires the balls horizontally and perpendicular to the diameter in opposite directions. After leaving the platform, the balls have horizontal speed of `9ms^(-1)` with respect to the ground. The rotational speed of the platform in `rad s^(-1)` after the balls leace the platform is
View SolutionA uniform circular disc of mass 1.5 kg and raius 0.5 m is initially ar rest on a horiozntal frictonless surface. Three forces of equal matgnitude F = 0.5 N are applied simultaneously along the three sides of an equilateral triangle XYZ with its vertices on the perimeter of the disc (see figure). One second after applying the forces the angular speed of the disc in `rad s^(-1)` is

View SolutionTwo identical uniform discs roll without slipping on tow different sufaces AB and CD (see figure) starting at A and C with linear speeds `v_1 and v_2` respectively, and always remain in contact with the surfaces. If they reach B and D with the same linear speed `v_1= 3m//s then v_2 in m//s is (g = 10 m//s^2)`

View SolutionThe densitis of two solid spheres A and B of the same radii R very with radial distance `r as p_A(r ) = k ((r )/(R )) and p_B(r ) = k((r )/(R )^5),` respectively, where k is a constant . The moments of inertia of the inividual spheres about axes passing throgh their centres are `I_A and I_B` respectively. if `(I_B)/(I_A) = (n)/(10),` the value of n is
View SolutionInitial angular velocity of a circualr disc of mass M is `omega_1.` The tow sphere of mass ma re attached gently to diametrically opposite points ont eh edge of the disc. What is the final angular velocity on the disc?
View SolutionThe minimum velocity (in ms^(-1))` with which a car driver must traverse a flat curve of radius 150m and coefficient of friction 0.6 to avoid skidding is
View Solution
JEE Main And Advanced questions and complete solutions for chapter ROTATIONAL MOTION of SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) of Class 11