Complete Solutions to EXAMPLE of chapter TEST 4 of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | TEST 4 |
| AAKASH INSTITUTE | EXAMPLE |
| Number Of Questions | 89 |
| Academic Year | 2023-24 |
The ratio of the density and pressure of a fixed mass of an ideal gas is "5" at 10°C. Then this ratio at 110°C is
View SolutionWhen a wave travels in a medium, the particle displacement is given by, y = psin2`pi`(qt - rx), where p, q and r are constants. The maximum particle velocity will be twice the wave velocity if
View SolutionA mixture of n1 moles of diatomic gas and n2 moles of monatomic gas has Cp/Cv = γ = 3/2, then
View SolutionThe Velocity of four gas molecules are given by 1 km/s, 2 km/s, 6 km/s and 8 km/s respectively. The rms velocity is
View SolutionA cylinder contains 12kg of gas at pressure of `10^7` N/`m^2`. The quantity of gas taken out of the cylinder, if final pressure is `3 xx 10^6 N//m^2` , will be (temperature of gas is constant)
View SolutionWhen sound wave is refracted from air to water, then which of the following quantity will change?
View SolutionThe equation y= A sin2(ωt - kx) represent a wave motion with amplitude and frequency as
View SolutionA closed vessel of volume `0.2m^3` contain hydrogen gas at temperature `300 K` and pressure `10^5 Pa`. Then the heat required to raise temperature to `600 K` is:(molar heat capacity of hydrogen at constant volume is `5 cal//mol-K`)
View SolutionThe molar heat capacity of a certain substance varies with temperature "T" as c = a + bT where a = 27.2 J mol-1 K-2. Then the heat necessary to change the temperature of 2 moles of this substance from 27°C to 427°C is
View SolutionTwo vessel having equal volume contain molecular hydrogen at one atmosphere and helium at two atmospheres respectively. What is the ratio of rms speed of hydrogen molecule to that of helium molecule? ( Assume both the samples are at same temperature)
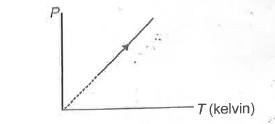
View SolutionThe graph of pressure and temperature for an ideal gas is as shown in figure. The given process is
View SolutionA particle of mass 0.2 kg exectites SHM under a force of F = - 20x N. If speed of particle at mean position is 12 m/s then the amplitude of oscillations is
View SolutionA simple pendulum has time period T_1. The point of suspension is now moved upward according to the relatiori. y = `kt^2` (k = 2 m/`s^2`) where y is the vertical displacement. The time period now becomes `T_2` then the ratio of `T_1^2`/`T_2^2` (g = 10 m/`s^2`)
View SolutionWhich of the following statement is incorrect?
View SolutionIf two SHMs are represented by equations `y_1`= 4 sin[3`pi`t + (`pi`/3)], `y_2`= 4 [sin(3`pi`t) +`sqrt 3` cos (3`pi`t)], then the ratio of their amplitudes is
View SolutionIf at `t = 0`, a travelling wave pulse on a string is described by the function.
`y = (6)/(x^(2) + 3)`
What will be the waves function representing the pulse at time `t`, if the pulse is propagating along positive x-axis with speed `4m//s`?
View SolutionTwo masses `m_(1) and m_(2)` are suspended together by a massless spring of constant k. When the masses are in equilibrium, `m_(1)` is removed without disturbing the system. Then the angular frequency of oscillation of `m_(2)` is
View SolutionA block of mass `m_1` resting on a frictionless horizontal surface is connected to a spring of spring constant k that is anchored in a near by wall. A block of mass `m_2` is placed on the top of the first block. The coefficient of static friction between the two blocks is `mu` Assuming that the two blocks move together as a unit, find the period of oscillation of the system and also find maximum oscillation amplitude that permits the two bodies to move as a unit.
View SolutionA body moves along a straight line OAB simple harmonically. It has zero velocity at the points A and B which are at distances 'a' and `b' respectively from `0' and has velocity 'V' when halfway between them then the period of SHM
View SolutionIf a spring of force constant 'k' is cut into two parts, such that one part is thrice in length of the other part. Then the force constant of each part are
View SolutionIf the fundamental frequency of a closed of pipe is equal to the first overtone of an open organ pipe then the ratio of lengths of closed organ pipe to open organ pipe is
View SolutionA coin is placed on a horizontal platform which undergoes vertical SHM of angular frequency `omega` . The amplitude of oscillation is gradually increased. The coin will leave contact with platform for the first time.
View SolutionA particle at the end of a spring executes SHM with a period `t_(1)`While the corresponding period for another spring is If the period of oscillation with the two springs in series is T, then :
View SolutionIf `v_1` and `v_2` denote the sound velocity'and root mean square velocity of molecules of an ideal gas then select the correct option (γ = adiabatic constant)
View SolutionWhen sound is produced in an aeroplane moving With a velocity of 200. m/s horizontally its echo is heard after 10`sqrt 5` seconds. If velocity of sound in air is 300 m`s^-1` theielevation of aeroplane is
View SolutionA simple harmonic progressive wave is represented by the equation- y = 8sin2`pi`(0.1x — 2t) , where x and y are in cm and t is in second. At any instant the phase difference between two particles separated, by 2.0 cm in the x direction is
View SolutionFor a certain organ pipe, three successive resonance frequencies are observed at 425, 595 and 765 Hz. The speed of sound in air is 340 m/s. The pipe is
View SolutionThe frequency of tuning forks A and B are respectively 5% more and 4% less than the frequency of tuning fork C. When A and B are simultaneously excited, 9 beats per second are produced. Then the frequency of the tuning fork A (in Hz) is
View SolutionTwo wires are in unison. If the tension in one of the wires is increased by 2%, 5 beats are produced per second. The initial frequency of each wire is
View SolutionA transverse wave pulse is generated at the free end of a string which is hanging from a rigid support. The speed of the wave pulse at distance x from the free end is proportional to
View SolutionThe stationary wave y = 2a sin kx cos`omega`t in a closed organ pipe is the result of the superposition of y = a sin( `omega`t — kx) and
View SolutionIn a resonance pipe the first and second resonances are obtained at depths 23.7 cm and 72.3 cm respectively. Then the end correction will be
View SolutionA person feels 2.5% difference of frequency of a motor-car horn. If the motor-car is moving towards the person and the velocity of sound is 320 m/s, then the velocity of motor car will be (approximately)
View SolutionIf the amplitude of sound is doubled and the frequency reduced to one- fourth the intensity of sound at the same point will
View SolutionIntensity level at a distance 200 cm frorn.a point source of sound is 80 dB. If there is it loss of acoustic power in air and intensity of tireshold hearing is `10^-12` W`m^-2`, then the intensity level at a distance of 4000 pm from source is (log 20` = 1.3)
View SolutionTwo cars are moving on two perpendicular roads towards a crossing with uniform speeds of 72 kmph and 36 kmph. If first car blows horn of frequency 300 Hz, then the frequency of horn heard by the driver of second car when line joining the cars make 45° angle with the roads will be (Speed of sound = 330 m/s)
View SolutionIn an experiment, sonometer wire vibrates in 4 loops when a 50 g weight is placed in the pan of weight 15 g. To make the wire vibrates in 6 loops the mass that has to be removed from the pan is approximately [frequency of vibration remains constant]
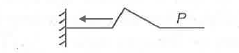
View SolutionGiven figure shows an incident pulse P reflected from a rigid support. Which one of following represents the reflected pulse correctly?
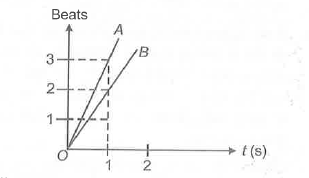
View SolutionTwo tuning forks P and Q are vibrated together. The number of beats produced are represented by the straight line OA in the following graph. After loading Q with wax again these are vibrated together and the beats produced are represented by the line OB. If the frequency of P is 341 Hz, then frequency of Q will be
View SolutionA string is rigidly tied at two ends and its equation of vibration is given by y = cos2`pi`tsin2`pi`x . Then minimum length of string is
View SolutionThe length of a sonometer wire is 0.75 m and density is 9 `xx` `10^3` kg/`m^3`. It can bear a stress of 8.1 `xx` `10^8` N/`m^2` without exceeding the elastic limit. Then the fundamental frequency that can be produced in the wire is
View SolutionThree waves of equal frequency having amplitudes 10 mm, 4 mm and 7 mm superpose at a given point with successive phase difference of `pi`/2 . The amplitude of the resulting wave in mm is given by
View SolutionA line source of sound of length 10 m, emitting a pulse of sound that travels radially outward from the source. The power of the source is P = 1.0.x `10^4` W What is the approximated intensity '/' of the sound when it reaches a distance of 10 m from the source?
View SolutionThe particles of a medium oscillate about their equilibrium position, whenever a wave travels through that medium. The phase difference between the oscillations of two such practices varies
View SolutionThe change in frequency due to Doppler effect does not depend on
View SolutionThe dimensional formula of "Moment of force" is
View SolutionThe direction of the angular velocity vector is along
View SolutionThe rotational inertia of a disc about its geometrical axis does not depend upon its
View SolutionA force with a given magnitude is to be applied to a wheel. The torque can be maximised by
View SolutionA particle, held by a string whose other end is attached to a fixed point C, moves in a circle on a horizontal frictionless surface. If the string is cut, the angular momentum of the particle about the point C
View SolutionA single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is
View SolutionTen seconds after an electric fan is turned on, the fan rotates at 300 rev/min. Its average angular acceleration is
View SolutionThe angular position of a point over a rotating flywheel is changing according to the relation, `theta = (2t^3 - 3t^2 - 4t - 5)` radian. The angular acceleration of the flywheel at time, t = 1 s is
View SolutionKeeping moment of inertia constant, the angular momentum of a body is increased by 20%. The percentage increase in its rotational kinetic energy is
View SolutionThe radius of gyration of a hollow sphere of radius R about an axis along its tangent is
View SolutionThe two arms of a balanced are of unequal length. An object when placed in the left pan of the balance weighs 4 kg. The same object when placed in the right pan of the balance weighs 9 kg. The actual (or) true mass of the object is
View SolutionTwo discs are mounted on frictionless bearings on a common shaft. The first disc has rotational inertia / and is spinning with angular velocity `omega`. The second disc has rotational inertia 2/ and is spinning in opposite direction with angular velocity `3omega`, as shown in figure. The two discs are slowly forced towards each other along the shaft until they couple and have a final common angular velocity of

View SolutionFrom a complete ring of mass `M` and radius `R`, a `30^@`sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,
,
View SolutionA rod is pivoted about its centre. A 10 N force is applied 4 m from the pivot and another force of 5 N is applied 2 m from the pivot, as shown. The magnitude of the total torque about the pivot is

View SolutionFind the moment of inertia of a uniform square plate of mass `M` and edge a about one of its diagonals.
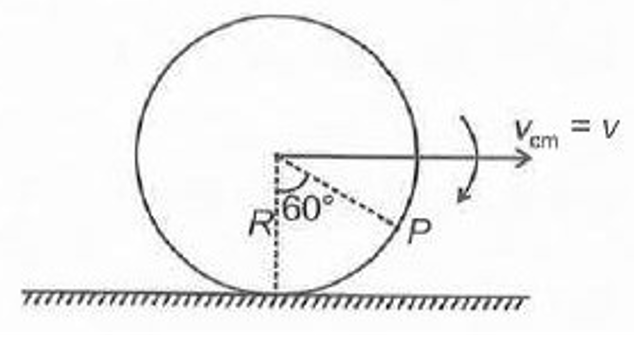
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
View SolutionThe moment of inertia of a thin square plate ABCD, fig, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
where `l_1, l_2, l_3 and l_4` are respectively the moments of intertial about axis 1,2,3 and 4 which are in the plane of the plate.
View SolutionA boy of mass 30 kg is standing at one end on a stationary boat over a lake. The boat has a mass 70 kg and length 10 m. Now the boy walked to the other end of the boat. Relative to the ground
View SolutionA uniform plank is supporeted by two equal 120 N forces at x and y as shown in figure. If the support at x is moved to z, then the supporting forces at y and z are
View SolutionA thin uniform wire of mass m and length l is bent into to shape of a semicircle. The moment of inertia of that wire about an axis passing through its free ends is
View SolutionA ring rolls down an inclined plane and acquires a velocity v upon reaching the bottom of the inclined plane. If another body rolls down from the same height over the same inclined plane and acquires a velocity `sqrtfrac{6}{5}v` upon reaching the bottom of the inclined plane, then that body is
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If `v_0` is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA 16 kg block is attached to a cord that is wrapped around the rim of a flywheel of diameter 0.4 m and hangs vertically, as shown in figure. The rotational inertia of the flywheel is 0.5 kg `m^2`. When the block is released and the cord unwinds, the acceleration of the block is

View SolutionA ring is rolling without slipping. The ratio of translational kinetic energy to rotational kinetic energy is
View SolutionA pulley with a radius of 3 cm and rotational inertia of `4.5xx10^-3` kg `m^2` is suspended from the ceiling. A rope passes over it with a 2 kg block attached to one end and a 4 kg block attached to the other. The rope does not slip on the pulley. At any instant after the blocks start moving, the object with the greatest kinetic energy is
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionThe moment of inertia of a solid sphere of radius R about an axis passing through its diameter is /. The sphere is melted and recast into a circular disc of thickness `frac{R}{3}`. The moment of inertia of this disc about an axis perpendicular to plane and passing through its centre of mass is
View SolutionA hollow sphere rolls down a rough inclined plane whose angle of inclination is `theta`, with horizontal. For the hollow sphere to undergo pure rolling, without slipping, the condition is [`mu` = coefficient of friction between the hollow sphere and inclined plane]
View SolutionA body of mass m is projected with a velocity u at an angle `theta` with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View SolutionThe centre of mass shifts by a distance S, when a square of side `frac{R}{2}` is cut from a uniform disc of radius R as shown in figure. The value of S is

View SolutionA particle of mass 300 g is moving with a speed of 20 `ms^-1` along the straight line y = x - `4sqrt2`. The angular momentum of the particle about the origin is (where y & x are in metres)
View SolutionA cubical block of edge length 1 m and density 800 kg `m^-3` rests on a rough horizontal surface with coefficient of friction `mu`. A horizontal force F is applied on the block as shown in figure. If the coefficient of friction is sufficiently large so that the block does not slide bofore toppling, then the minimum value of F to topple the block is [Take g = 10 `ms^-2`]

View SolutionA body is thrown from ground for horizontal range 100 m. If the body breaks into two fragments of mass in the ratio `1 : 2` at the highest point and smaller mass stops there and comes vertically downward, then horizontal range of the centre of mass of the body is
View SolutionA body is in pure rolling over a horizontal surface. If the rotational kinetic energy of that body is 40% of its total kinetic energy, then the body is
View SolutionA particle is rotating about a fixed axis with angular acceleration `vecalpha = hati + 2hatj + 3hatk` rad/`s^2`. Find the tangential acceleration of a point having radius vector `(2hati-3hatj+hatk)`m from axis of rotation in (in m/`s^2`)
View SolutionTwo discs A and B have same mass and same thickness. If `d_1` and `d_2` are the densities of the materials of the discs A and B respectively, then the ratio of the moment of inertia of the discs A and B about their geometrical axis is
View SolutionThe rotational inertia of a disc about its axis is 0.70 kg `m^2`. When a 2.0 kg mass is added to its rim, 0.40 m from the axis, the rotational inertia becomes
View SolutionA force `vecF = (hati+hatj-hatk)N` acts at a point P(3 m, 6 m, 9 m). The torque exerted by this force about a point Q(2 m, 7 m, 8 m) is
View SolutionA pulley with a radius of 3 cm and rotational inertia of `4.5xx10^-3` kg `m^2` is suspended from the ceiling. A rope passes over it with a 2 kg block attached to one end and a 4 kg block attached to the other. The rope does not slip on the pulley. At any instant after the blocks start moving, the object with the greatest kinetic energy is
View SolutionThe angular velocity of a wheel rotating with constant angular acceleration, changes from 2 rad/s to 6 rad/s in a time interval of 31.4 s. The number of rotations made by the wheel in this interval of time is
View SolutionA man stands on a rotating platform with his arms stretched holding a 5 kg weight in each hand. The angular speed of the platform is `1.2 rev s^(-1)`. The moment of inertia of the man together with the platform may be taken to be constant and equal to `6 kg m^(2)`. If the man brings his arms close to his chest with the distance of each weight from the axis changing from 100 cm to 20 cm . The new angular speed of the platform is
View SolutionA wheel initially has an angular velocity of 18 rad/s. It has a costant angular acceleration of 2 rad/`s^2` and is slowing at first. What time elapses before its angular velocity is 22 rad/s in the direction opposite to its initial angular velocity?
View SolutionFor a body to be in equilibrium under the combined action of several forces
View SolutionThe SI unit of "Angular Impulse" is
View Solution
EXAMPLE questions and complete solutions for chapter TEST 4 of AAKASH INSTITUTE ENGLISH of Class 12