Complete Solutions to Illustration of chapter CHEMICAL KINETICS of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | CHEMICAL KINETICS |
| CENGAGE CHEMISTRY | Illustration |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The decompoistion of `N_(2)O_(5)` in `C CI_(4)` solution at `318 K` has been studied by monitoring the concentration of `N_(2)O_(5)` in the solution. Initially, the concentration of `N_(2)O_(5)` is `2.33 M` and after `184 min`, it is reduced to `2.08 M`. The reaction takes place according to the equation:
`2N_(2)O_(5) rarr 4NO_(2) + O_(2)`
Calculate the average rate of this reaction in terms of hours, minutes, and seconds. What is the rate of Production of `NO_(2)` during this period?
View SolutionExpress the rate of the following reactions:
(a) `PCl_(5) rarr PCl_(3) + Cl_(2)`
(b) `2NO_(2) rarr 2NO + O_(2)`
in terms of the concentrations of reactants and Products.
View SolutionFor each of the following reactions, express the given rate of change of concentration of the reactants or Products in that reaction:
a.`H_(2)O_(2) + 2H^(o+) + 3l^(ɵ) rarr I_(3)^(ɵ) + 2H_(2)O`, `(-d[I^(ɵ)])/(d t) = ?`, `(-d[H^(o+)])/(d t) ? `
(b) `16H^(o+) + 2Mn_(4)^(ɵ) + 101^(ɵ) rarr 2Mn^(2+) + 8H_(2)O + 5I_(2)`, `(-d[MNO_(4)^(ɵ)])/(d t) = ?`
( c) `4NH_(3) + 5O_(2) rarr 4NO_(2) + 6H_(2)O` , `(-d[NH_(3)])/(d t) = ?`
View SolutionFor the reaction `4NH_(3) + 5O_(2) to 4NO + 6H_(2) O`, if the rate of disappearance of `NH_(3)` is `3.6 xx 10^(-3)` mol `L^(-1) s^(-1)`, what is the rate of formation of `H_(2) O`
View SolutionThe following reaction was carried out in water :
`Cl_(2) + 2I^(ɵ) rarr I_(2) + 2Cl^(ɵ)`
The initial concentration of `I^(ɵ)` was `0.25 mol L^(-1)` and the concentration after `10 min` was `0.23 mol L^(-1)`. Calculate the rate of disappearance of `I^(ɵ)` and rate of appearance of `I_(2)`.
View SolutionFor a reaction `Rto P`, the concentration of a reactant changes from 0.03 M to 0.02M in 25 minutes. Calculate the average rate of the reaction using the units of seconds.
View SolutionIn the following reaction, how is the rate of appearance of the underlined Product related to the rate of disappearance of the underlined reactant ?
`BrO_(3)^(ɵ)(aq) + 5underline(Br)^(ɵ)(aq) + 6H^(o+) (aq) rarr 3underline(Br_(2))(l) + 3H_(2)O(l)`
View SolutionFor the reaction
`H_(2) (g)+I_(2)(g) rarr 2HI(g)`, the rate of disappearance of `H_(2)` is `1.0 xx 10^(-4) mol L^(-1) s^(-1)`. The rate of appearance of `HI` will be
View SolutionThe rate of a reaction is expressed in different ways as follows:
`+(1)/(2)(d[C])/(dt)=-(1)/(3)(d[D])/(dt)=+(1)/(4)(d[A])/(dt)=-(d[B])/(dt)`
the reaction is
View SolutionThe term `-dx//dt` in the rate expresison refers to the
View SolutionIn a catalyst experiment involving the Haber process `N_(2) + 3H_(2) rarr 2NH_(3)`, the rate of reaction was measured as
Rate `= (Delta[NH_(3)])/(Delta t) = 2.0 xx 10^(-4) mol L^(-1) s^(-1)`
What is the rate of reaction expressed in terms of (a) `N_(2)` (b) `H_(2)` ?
View SolutionThe approach to the following equilibrium was observed kinetically form both directions:
`[PtCl_(4)]^(2-) +H_(2)O hArr [Pt(H_(2)O)Cl_(3)]^(ɵ)+Cl^(ɵ)`
At `25^(@)C` it was found that at `0.3` inoic strength `- (Delta [PtCl_(4)]^(2-))/(Delta t) = (3.9 xx 10^(-5)s^(-1))[PtCl_(4)]^(2-)`
`- (2.1 xx 10^(-3) L mol^(-1) s^(-1))[Pt(H_(2)O)Cl_(3)]^(ɵ)[Cl_(3)^(ɵ)]`
What is the value of `k` for the complexation of the fourth `Cl^(ɵ)` by `Pt(II)` at `0.3` ionic strength.
View SolutionWhich of the following expression can be used to describe the instantaneous rate of the reaction ?
`2A+B rarr A_(2)B`
(a) `(1)/(2)(-d[A])/(d t)`
(b) `(-d[A])/(d t)`
(c) `(1)/(2) (d[A_(2)B])/(d t)`
(d) `(1)/(2) (-d[A])/(d t).(d[B])/(d t)`
View SolutionWhich of the following will react at the highest rate ?
View SolutionThe reaction between `Cr_(2)O_(7)^(2-)` and `HNO_(2)` in an acidic medium is
`Cr_(2)O_(7)^(2-) + 5H^(o+) + 3HNO_(2) rarr 2Cr^(3+) + 3NO_(3)^(ɵ) + 4H_(2)O`.
The rate of disappearance of `Cr_(2)O_(7)^(2-)` is found to be `2.4 xx 10^(-4) mol L^(-1) s^(-1)` during measured time interval. What will be the rate of disappearance of `HNO_(2)` during the same time interval?
(a) `2.4xx10^(-4)`
(b) `7.2xx10^(-4)`
(c) `4.8xx10^(-4)`
(d) `0.8xx10^(-4)`
View SolutionThe complexation of `Fe^(2+)` with the chelating agent dipyridyl has been studied Kinetically in both the forward and reverse direction, For the complexation reaction `Fe^(2+)+3` dipy `rarr [Fe(dipy)_(3)]^(2+)`, the rate of formation of the complex at `25^(@)C` is given by
Rate `= (1.45 xx 10^(13) L^(3) mol^(-3) s^(-1)) [Fe^(2+)][dipy]^(3)` and for the reverse of the above eqaution, the rate of disappearance of the complex is
`(1.22 xx 10^(-4) s^(-1)) [Fe(dipy)_(3)]^(2+]`
What is `K_(s)`, the stability constant for the complex ?
View SolutionFor the reaction at `273 K`
`NO(g) + O_(3)(g) rarr NO_(2)(g) + O_(2)(g)`
It is observed that the pressure of `NO(g)` falls form `700 mm Hg` to `500 mm Hg` in `250 s`. Calculate the average rate of reaction in (a) `atm s^(-1)` , (b) `mol L^(-1) s^(-1)`.
View SolutionThe hydrogenation of vegetable ghee at `25^(@)C` reduces the pressure of `H_(2)` form `2 atm` to `1.2 atm` in `50min`. Calculate the rate of reaction in terms of change of
(a) Pressure per minute
(b) Molarity per second
View SolutionFor gaseous reactions, the rate is expressed in terms of `dP//dt` instead of `dc//dt` or `dn//dt` (where `c` is the concentration and `n` the number of `mol`). What is the relation among these expresisons ?
View SolutionIn the reaction, `2H_(2)O_(2) rarr 2H_(2)O + O_(2)` The rate of decomposition of `H_(2)O_(2)` is `0.68 kg hr^(-1)`. What is the rate of formation of `O_(2)` ?
View SolutionCalculate the overall order of a reaction which has the rate expresison.
(a) Rate`= k[A]^((1)/(2))[B]^((3)/(2))` , (b) Rate `= k[A]^((3)/(2))[B]^(-1)`
View SolutionFrom the rate laws for the reactions given below, determine order with order to each species and the overall order:
`2HCrO_(4)^(ɵ) + 6l^(ɵ) + 14H^(o+) rarr 2Cr^(3+) + 3I_(2) + 8H_(2)O`
Rate `= k[HCrO_(4)^(ɵ) ][I^(ɵ) ]^(2) [H^(o+)]^(2)`
View SolutionThe rate constant for the reaction, `2N_(2)O_(5) to 4NO_(2) + O_(2)` is `2 xx 10^(-5) s^(-1)`. If rate of reaction is `1.4 xx 10^(-5) mol L^(-1), s^(-1)` What will be the concentration of `N_(2)O_(5)` in mol `L^(-1)`?
View SolutionThe decompoistion of ammonia on platinum surface follows the change
`2NH_(3) rarr N_(2) + 3H_(2)`
If the decomposition is zero order then what are the rates of Production of `N_(2)` and `H_(2)` if `k = 2.5 xx 10^(-4) M s^(-1)` ?
View SolutionThe rate constant for the reaction:
`CO_(2) + overset(ɵ)(OH) rarr HCO_(3)^(ɵ)`
in the aqueous solution is `4 xx 10^(-3) L mol^(-1) s^(-1)`. The number of mole per volume of `CO_(2)` and `overset(ɵ)(OH)` are `10^(-6)` and `10^(-1) mol L^(-1)`. Also predict the mole of `HCO_(3)^(ɵ)` formed per second.
View SolutionFor a reaction `3A rarr` Products, it is found that the rate of reaction doubles. If the concentration of `A` is increased four times, calculated the order of reaction.
View SolutionThe rate of a reaction starting with initial concentration of `2 xx 10^(-3)` and `1 xx 10^(-3) M` are equal to `2.40 xx 10^(-4)` and `0.60 xx 10^(-4) M s^(-1)`, respectively. Calculate the order or reaction w.r.t. reactant and also the rate constant.
View SolutionThe reaction `2A + B + C rarr D + 2E` is found to be first order in `A`, second order in `B` and zero order in `C`.
(a) Write the rate expresison.
(b) What is the effect on rate on increaisng the concentration of `A, B`, and `C` two times ?
View SolutionFor `2A underset((excess)+ B + C rarr` Products, calculate:
(a) Rate expresison, uisng rate law.
(b) Units of rate and rate constant.
(c ) Effect on rate, if the concentration of `A` is doubled and that of `B` is tripled.
View SolutionThe rate of reaction: `2NO(g) + Cl_(2) (g) rarr 2NOCl (g)`, becomes doubled when the concentration of `Cl_(2)` is doubled. However, when the concentration of both the reactants are doubled, the rate becomes eight times. What is the order w.r.t. `NO` and w.r.t. chlorine ? What is the total order?
View SolutionShow by uisng rate laws how much the rate of reaction `2NO(g) + O_(2)(g) rarr 2NO(g)` will change if the volume of the reaction vessel is diminished to `1//3` of its initial volume.
View SolutionWhat would be the effect on the rate of reaction due to the four-fold increase in a reactant concentration, if the order of reaction were the following:
(a) Zero order , (b) First order
( c) `1//2` order , (d) Fourth order
View SolutionThe experiment rate law for the reaction `S_(2)O_(8)^(2-)(aq) + 2I^(ɵ)(aq) rarr 2SO_(4)^(2-) (aq) + I_(2)(aq)` is `k[S_(2)O_(8)^(2-)] [I^(ɵ)]`. How would the rate change if
(a) Concentration of `S_(2)O_(8)^(2-)` is halved.
(b) Concentration of `S_(2)O_(8)^(2-)` and `I^(ɵ)` are halved.
View SolutionFor the reaction `A + B rarr C + D`, doubling the concentration of both the reactants increases the reaction rate by `8` times and doubling the initial concentration of only `B` ismply doubles the reaction rate. What is the rate law for the reaction ?
View SolutionFor the non-equilibrium process, `A + B rarr` Product, the rate is first-order w.r.t. `A` and second order w.r.t. `B`. If `1.0 mol` each of `A` and `B` were inrofuced into `1.0 L` vessel and the initial rate was `1.0 xx 10^(-2) mol L^(-1) s^(-1)`, calculate the rate when half the reactants have been turned into Products.
View SolutionThe rate constant in numerically the same for the theee reaction of first, second, and third order. Which reaction should be the fastest and it this true for all ranges of concentrations?
View SolutionThe rate law for the following reactions:
`Ester + H^(o+) rarr "Acid" + "Alcohol"`, is
`dx//dt = k(ester)[H_(3)O^(o+)]^(0)`
What would be the effect on the rate if
(a) concentration of ester is doubled.
(b) concentration of `H^(o+)` ion is doubled.
View SolutionMechanism of the reaction is:
`A_(2) underset(k')overset(k)hArr 2A`
`A + B_(2) overset(k_(2))rarr C + B`
`B + A_(2) overset(k_(2))rarr C + A`
What is`(-d[A_(2)])/(dt)`
View SolutionMechanism of the reaction is:
`A overset(k_(1))rarrB, 2Aoverset(k_(2))rarr C + D`
What is `(-d[A])/(dt)` ?
View SolutionMechanism of the reaction is:
What is `(-d[A])/(dt)` ?
View SolutionMechanism of the reaction is:
`A underset(k_(1))overset(k_(2))hArr B` ...(i)
`B+A overset(k_(3))hArr C` ...(ii)
`ul(bar(2A rarr C))` ...(iii)
What is (a) `(-d[A])/(dt)`, (b ) `(d[C])/(dt)`
View SolutionMechanism of the reaction is:
`A_(2) overset(k_(2))hArr 2A`
`A + B overset(k_(2))rarr C`
`A_(2) + C overset(k)rarr D + A`
What is `(d[D])/(dt)` ?
View SolutionThe rate of the reaction
`2N_(2)O_(5) to 4NO_(2) + O_(2)`
can be written in three ways:
`(-d[N_(2)O_(5)])/(dt)=k[N_(2)O_(5)]`
`(d[NO_(2)])/(dt)=k'[N_(2)O_(5)]`
`(d[O_(2)])/(dt)=k''[N_(2)O_(5)]`
The relationship between k and k′ and between k and k′′ are-
View Solution`2SO_(2) + O_(2) underset(k_(2))overset(k_(1))hArr 2SO_(3)`
What are the expresison for the rate law of the forward and backward reactions?
View SolutionMechanism of the reaction is:
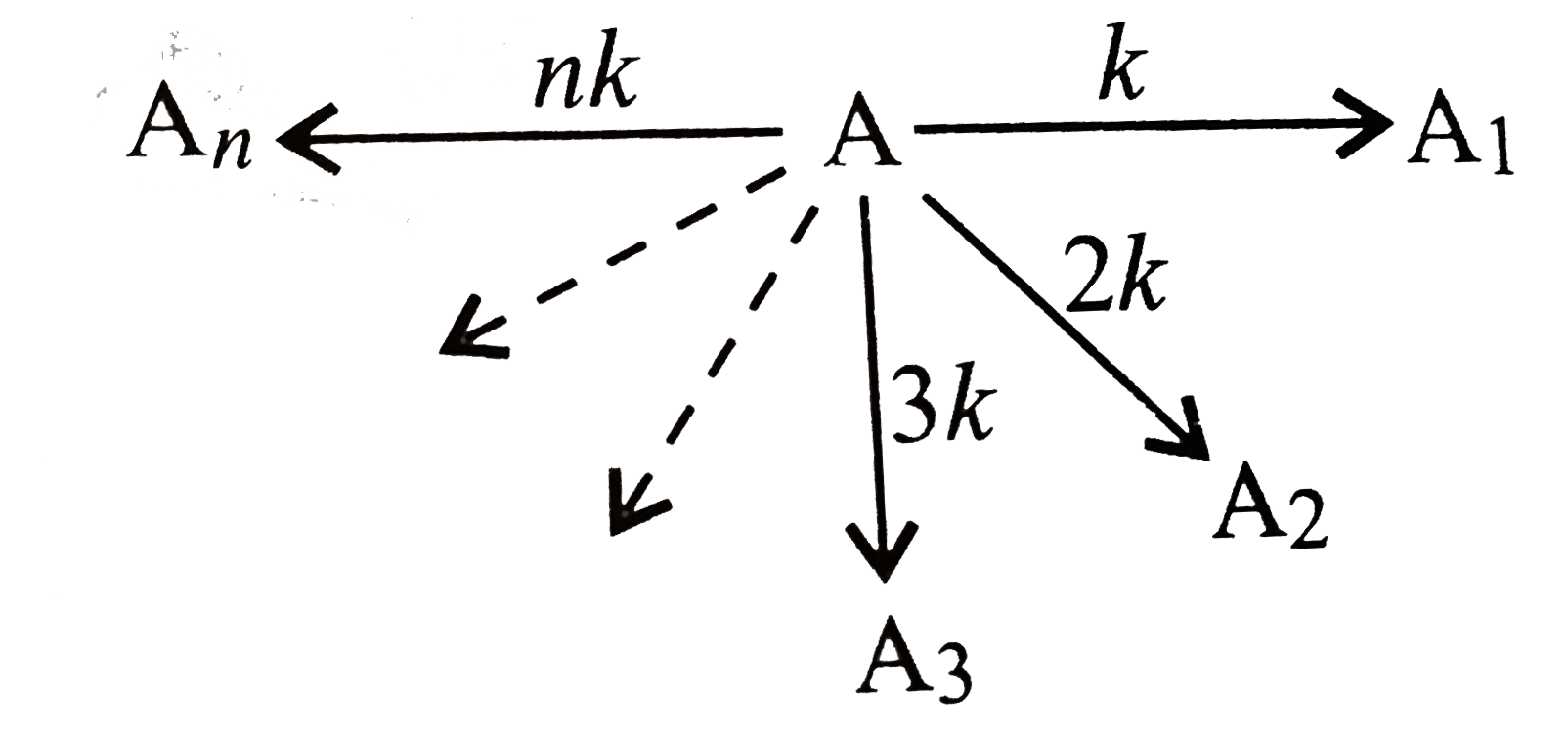
What is (a) `(-d[A])/(dt)`, (b) `(d[A_(1)])/(dt)`
View SolutionThe following equilibria are given by
rho`N_(2)+3H_(2)hArr2NH_(3):K_(1)`
`N_(2)+O_(2)hArr2NO,K_(2)`
`H_(2)+1/2O_(2)hArrH_(2)O,K_(3)`
The equlibrium constant of the reaction
`2NH_(3)+5/2O_(2)hArr2NO+3H_(2)O`
in terms of `K_(1) and K_(3)` is
View SolutionThe termolecular reaction
`2NO(g) + H_(2)(g) rarr 2NOH(g)` is found to be third order obeying the rate law `r = k[NO]^(2)[H_(2)]`. Show that it is conisstent with either of the following mechanisms:
(a) `2NO(g) overset(k_(eq))hArr N_(2)O_(2)(g) ("fast equilibrium")`
`N_(2)O_(2)(g) + H_(2)(g) overset(k')rarr 2NOH(g)` (slow)
(b) `2NO(g) +H_(2)(g) overset(k'_(eq))hArr NOH_(2)(g) ("fast equilibrium")`
`NOH_(2)(g) + NO(g) overset(k'')rarr 2NOH(g)` (slow)
View SolutionFor and elementary reaction
`2A underset(k_(2))overset(k_(1))hArr B`, the rate of disappearance of `A` iss equal to
(a) `(2k_(1))/(k_(2))[A]^(2)`
(b) `-2k_(1)[A]^(2) + 2k_(2)[B]`
( c) `2k_(1)[A]^(2) - 2k_(2)[B]`
(d) `(2k_(1) - k_(2))[A]`
View SolutionConisder the following reactions:
I. `A+B underset(k_(-1))overset(k_(1))hArr C`
II. `C + B overset(k_(2))rarr D`
Then `k_(1)[A][B]-k_(-1)[C]-k_(2)[C][B]` is equal to
(a) `(-d[A])/(dt)`
(b)`(-d[B])/(dt)`
(c)`(d[C])/(dt)`
(d)`(d[D])/(dt)`
View SolutionThe rate expression of some reactions are given below. Propose a probable mechanism of each of the following reactions:
(a) `2N_(2)O_(5) rarr 4NO_(2) + O_(2)`, Rate `= k[N_(2)O_(5)]`
(b) `2NO_(2) + F_(2) rarr 2NO_(2)F`, Rate `= k [NO_(2)][F_(2)]`
View SolutionIn the following reaction:
`2NO(g)+O_(2)(g) overset(k')rarr2NO_(2)(g)`
What is the predicted rate law, if the mechanism is
`NO+O_(2)(g) overset(k_(eq))hArr NO_(3) ("fast")` (fast)
`NO_(3) + NO overset(k_(1))rarr NO_(2) + NO_(2)` (slow)
View SolutionA reaction is found to proceed in two steps as `A + B rarr E` (slow),, `A+E rarr C+D` (fast). Write the law expresison and overall balanced equation.
View SolutionA chemical reaction proceeds as follows:
`A + C rarr D + F` (Slow)
`F + B rarr G` (Fast)
`G + C rarr E` (Fast)
Suggest rate law,units for rate constant, and overall reaction.
View SolutionFor the chemical reaction:
`5Br^(ɵ) + BrO_(3)^(ɵ) + 6H^(o+) rarr 3Br_(2) + 3H_(2)O`
Rate `= k[Br^(ɵ)] [BrO_(3)^(ɵ)] [H^(o+)]`
What is the molecularity and order of reaction with respect to `[Br^(ɵ)]` ?
View SolutionFor the chemical reaction
`I^(ɵ) + OCl^(ɵ) rarr Cl^(ɵ) + OI^(ɵ)`
Rate `= (k[OCl^(ɵ)] [I^(ɵ)])/([overset(ɵ)(OH)]`
What is the order and molecularity of the reaction ?
View SolutionThe chemical reaction, `2O_(3) to 3O_(2)` proceeds as
`O_(3) hArr O_(2) + [O]` (fast)
`[O] + O_(3) to 2O_(2)` (slow)
The rate law expression will be
View SolutionUsing the following data, calculate the value of equilibrium constant for the following reaction at `298K`
`underset("Acetylene")(3HC-=CH)hArr underset("Benzene")(C_(6)H_(6)(g))`
Assuming ideal behaviour
`Delta_(f)G^(Theta) (HC-= CH) = 2.09 xx 10^(5) J mol^(-1)`
`Delta_(f)G^(Theta) (C_(6)H_(6)) = 1.24 xx 10^(5) J mol^(-1)`,
`R = 8.314 J K^(-1) mol^(-1)`
Can the reaction be recommended for the synthesis of benzene?
View SolutionThe `E_("cell")` of the reaction
`MnO_(4)^(-)+Fe^(+2)+H^(+)rarrMn^(2+)+H_(2)O` is 0.59 V at `25^(@)C` The equilibrium constant for the reaction is
View SolutionDeduce the rate law for the converison of `H_(2)` and `I_(2)` to `HI` at `440^(@)C` corresponding to the following proposed mechanism:
step I: `I(2) hArr 2I^-1 ("fast") (k_(1))`
Step II: `I^-1+H_(2) hArr IH_(2) ("fast") (k_(2))`
Step III: `IH_(2) + I^-1 rarr 2HI` (slow) `(k)`
View SolutionFigure shows two shells of masses `m_1` and `m_2` . The shells are concentric. At which point, a particle of mass m shall experience zero force?
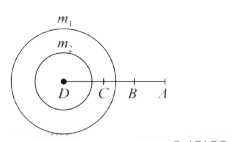
View SolutionThe initial concentration of `N_(2)O_(5)` in the following first order reaction ltBRgt `N_(2)O_(5)(g) rarrNO_(2)(g)+2O_(2)(g)` Was `1.24xx10^(-2) ''mol''L^(-1) "at" 318 k.` The concentration of `N_(2)O_(5)` after 60 min was `0.20xx10^(-2)molL^(-1)` The
Calculate the rate constant of the reaction art 318 K.
View SolutionA first order reaction is found to have a rate constant, `k = 5.5 × 10^(-14) s^(-1)`. Find the half-life of the reaction.
View SolutionShow that in case of a first order reaction, the time required for `99.9%` of the reaction to take place is about `10` times that the required for half the reaction.
View SolutionFor a first order reaction, time taken for half of the reaction to complete is `t_(1)and 3/4` of the reaction to complete is `t_(2)`. How are `t_(1)and t_(2) related?
View SolutionIdentify the reaction order form each of the following rate constants:
a. `k = 7.06 xx 10^(-3) mol L^(-1) s^(-1)`
b. `k = 5.6 xx 10^(-5) s^(-1)`
c. `k = 1.25 xx 10^(-2) mol^(-1)l s^(-1)`
d. `k = 1.25 xx 10^(-2) mol L^(2)s^(-1)`
e. `k = 5.0 xx 10^(-6) atm^(-1)s^(-1)`
View SolutionFor the reaction:
`2A+Bto A_(2)B`
the rate = `k[A][B]^(2)` with k `= 2.0xx10^(-6) mol^(-2) L^(2)s^(-1)`. Calculate the initial
rate of the reaction when `[A] =0.1 mol L^(-1),[b] = 0.2mol L^(-1)`. Calculate
the rate of reaction after [A] is reduced to `0.06 mol L^(-1)`
View SolutionA drug becomes ineffective after `30%` decompoistion. The original concentration of a sample was `5 mg mL^(-1)` which becomes `4.2 mg mL^(-1)` during `20` months. Assuming the decompoistion of first order, calculate the expiry time of the drug in month. What is the half life of the Product?
View SolutionThe half life of a first order reaction is `60 min`. How long will is take to consume `90%` of the reactant?
View SolutionThe rate constant of a first order reaction is `15 xx 10^(-3) s^(-1)`. How long will 5.0g of this reactant take to the reduce to 3.0 g?
View SolutionIf in a reaction `A rarr` Products, the concentrations of reactant `A` are `c_(0), ac_(0), a^(2)c_(0) a^(3)c_(0)`, …after time interval `0,t,2t,3t`…. Where `a` is constant, given, `0 lt alt 1`, show that the reaction is of first order. Also calculate the relation in `k, a`, and `t`.
View SolutionFigure shows a wire ring of radius a that is perpendicular to the general direction of a radially sysmmetric, diverging magnetic field. The magnetic field at the ring is everywhere of the same magnitude B, and its direction at the ring everywhere makes an angle `theta` with a normal to the plane of the ring. thge twisted lead wires have no effect on the problem. Find the magnitude of the force the field exerts on the ring if the ring carries a current i.

View SolutionFor the reaction of I, II and III orders, `k_(1) = k_(2) = k_(3)` when concentrations are expressed in mole `L^(-1)`. What will be the relation in `k_(1), k_(2), k_(3)`, if the concentration are expressed in `mol mL^(-1)`?
View SolutionStarting with one mole of a compound `A`, it is found that the reaction is `3//4` completed in `1 hr`. Calculate the rate constant if the reaction is of
a. First order , b. Second order
View SolutionIn the pure inductive circuit, the curves between frequency f and reciprocal of inductive reactance `1//X_(L)` is
View SolutionA drop of solution (volume `0.05 mL`) contains `3 xx 10^(-6) "mole" H^(o+)` ions. If the rate constant of disappearance of `H^(o+)` ions is `1 xx 10^(7) mol L^(-1) s^(-1)`, how long would it take for `H^(o+)` ions in the drop of disappear?
View SolutionFor a reaction , a graph was plotted between reactant concentration `c` and time as shown in the figure below.

Identify the order of the reaction with respect to the reactant. Can the concentration of the reactant be theoretically zero after infinite time?
View Solution`2A + 3B rarr `Product
a. What is the molecularity of the reaction?
b. What is order w.r.t. `A` and `B` in the following cases:
When `((dx)/(dt)) = k[A]` and `B` is in excess.
View SolutionFor the hypothetical reaction
`2A + B rarr` Products
following data obtained:
`|{:("Experiment number","Initial conc of (A)" (mol L^(-1)),"Initial conc of (B)" (mol L^(-1)),"Initial rate mol" L^(-1) s^(-1),),(1,0.10,0.20,3 xx 10^(2),),(2,0.30,0.40,3.6 xx 10^(10^(3)),),(3,0.30,0.80,1.44 xx 10^(4),),(4,0.10,0.40,...,),(5,0.20,0.60,...,),(6,0.30,1.20,...,):}|`
Find out how the rate of the reaction depends upon the concentration of `A` and `B` and fill in the blanks given in the table.
View SolutionThe data for the reaction: `A + B overset(k)rarr C`.
`|{:("Experiment",[A]_(0),[B]_(0),"Initial rate"),(1,0.012,0.035,0.10),(2,0.024,0.070,0.80),(3,0.024,0.035,0.10),(4,0.012,0.070,0.80):}|`
The rate law corresponding to the above data is
(a) Rate `= k[B]^(3)` , (b) Rate `= k[B]^(4)`
( c) Rate `= k[A][B]^(3)` , (d) Rate `= k[A]^(2)[B]^(2)`
View SolutionRate of a reaction `A + B rarr` Product, is given as a function of different initial concentration of `A` and `B`.
`|{:([A] (mol L^(-1)),(B) (mol L^(-1)),"Initial rate" (mol L^(-1) min^(-1)),),(0.01,0.01,0.005,),(0.02,0.01,0.010,),(0.01,0.02,0.005,):}|`
Determine the order of the reaction with respect to `A` and with respect to `B`. What is the half life of `A` in the reaction ?
View SolutionFor a reaction in which `A` and `B` form `C`, the following data were obtained form theee experiments:
What is the rate equation of the equation and what is the value of rate constant ?
View SolutionThe chemical reaction between mercuric chloride and potasisum oxalate proceeds as under:
`2HgCl_(2) + K_(2)C_(2)O_(4) rarr KCl + 2CO_(2) + Hg_(2)Cl_(2)`
The mass of `Hg_(2)Cl_(2)` precipitated form different solutions in a given time at `100^(@)C` was as follows:
`|{:("Experiment number",HgCl_(2) (mol L^(-1)),K_(2)C_(2)O_(4) (mol L^(-1)),"Time (min)",Hg_(2)Cl_(2) "precipitated (mole)"),(1,0.0836,0.404,65,0.0068),(2,0.0836,0.202,120,0.0031),(3,0.0418,0.404,60,0.0032):}|`
form the data calculate order of the reaction.
View SolutionA certain radio isotope `._(Z)X^(A)` (half life `= 10 ` days) decays to give `._(Z-2)Y^(A-4)` . If `1.0 g` atom of `X` is kept in a sealed vessel, find the volume of helium accumulated at `STP` in `20` days ?
View SolutionThe population of India in 1998 was `800` million. What will be the population in `2000` if there is no change in the present growth rate which is `25` per `1000` per year?
View SolutionThe experiment data for the reaction `2A + B_(2) rarr 2AB` is
`|{:("Experiment",[A] M,[B_(2)] M,"Initial rate" (mol L^(-1) s^(-1)),),(I,0.50,0.5,1.6 xx 10^(-4),),(II,0.50,1.0,3.2 xx 10^(-4),),(III,1.00,1.0,3.2 xx 10^(-4),):}|`
Write the most probable rate equation for the reacting giving reason for you answer.
View Solutionform the gaseous reaction
`2A + B_(2) rarr 2AB`, the following rate data were obtained at `300 K`.

Calculate the rate constant for the reaction and the rate of formation of `AB` when `[A]` is `0.02` and `[B_(2)]` is `0.04 mol L^(-1)` at `300K`.
View SolutionFor a chemical reaction `A rarr` Products, the rate of reaction doubles when the concentration of `A` is increased by `4` times. The order of reaction is
View SolutionFor a hypothetical reaction `A + B rarr C`, suggest the rate law and order form the following data:
`|{:("Experiment",[A] (mol L^(-1)),[B] (mol L^(-1)),"Refer of reaction" (mol L^(-1) s^(-1)),),(I,0.25,0.25,3.0 xx 10^(-3),),(II,0.50,0.25,6.0 xx 10^(-3),),(III,0.50,0.50,1.20 xx 10^(-2),):}|`
View SolutionFor the chemical reaction
`A + B + C rarr E`,
The rate of reaction is doubled when the concentration of `B` was doubled, and when the concentration of both `A` and `B` were doubled the rate becomes doubled and when the concentration of both `B` and `C` were doubled the rate becomes quardrupled. What is order with respect `A, B`, and `C` and total order?
View SolutionFor the chemical reaction `A + 2B rarr C`, the rate of reaction is increased by `2.82` times when the concentration of `A` is doubled and increased by `9` times when the concentration of `B` was tripled. What is the order with respect to `B` and `A` and total order ?
View SolutionThe rate of a gaseous reaction is given by the expression `k[A]^(2)[B]^(3)`. The volume of the reaction vessel is reduced to one half of the initial volume. What will be the reaction rate as compared to the original rate a?
View SolutionFor a chemical reaction, `X to Y` the rate of reaction increases by a factor of 1.837 when the concentration of X is increased by 1.5 times, the order of the reaction with respect to X is
View SolutionThe rate of the reaction
`3A + 2B rarr` Products
is given by the rate expresison: Rate `= k[A][B]^(2)`
If `A` is taken in excess, the order of the reaction would be
View SolutionFor the decompoistion of `HI` at `1000 K(2HI rarr H_(2)+I_(2))`, following data were obtained:
`|{:([HI] (M),"Rate of decomposition of HI" (mol L^(-1) s^(-1))),(0.1,2.75 xx 10^(-8)),(0.2,11 xx 10^(-8)),(0.3,24.75 xx 10^(-8)):}|`
The order of reaction is
View SolutionWhat will be the initial rate of a reaction if its rate constant is `10^(-3) min^(-1)` and the concentration of reactant is `0.2 mol dm^(-3)` ? How much of reactant will be converted into Products in `200 min`?
View SolutionWhich of the following graph is correct for a zero order reaction ?
View SolutionUsing the given graph showing concentration of reactants and Products as a function of times for the reaction:
`A_(3) rarr 3A`
The time `t_(1)` corresponds to
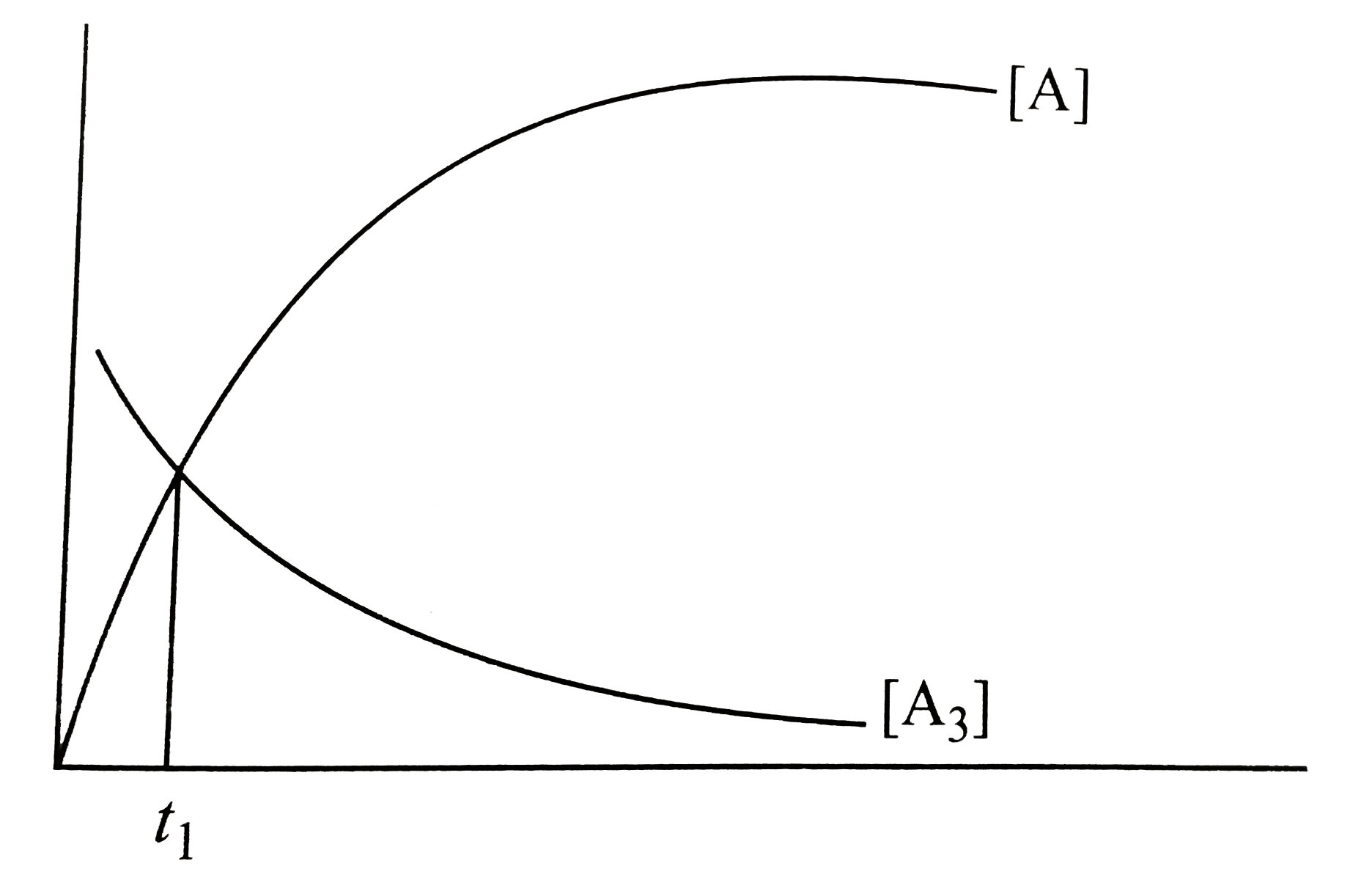
View SolutionThe plot of In `(c_(0))/(c_(0)-x)` against `t` is a straight line, showing the reaction to be a
View SolutionIf a soup has pH 6.7. What would be its taste?
View SolutionThe half-life period and initial concentration for a reaction are as follows. What is order of reaction ?
`|{:("Initial concentration (M)",350,540,158),(t_(1//2) (hr),425,275,941):}|`
View Solution
Illustration questions and complete solutions for chapter CHEMICAL KINETICS of CENGAGE CHEMISTRY (ENGLISH) of Class 12
All Exercises from CENGAGE CHEMISTRY Class 12 CHEMISTRY CHEMICAL KINETICS
- Archives Fill In The Blanks
- Archives Integer
- Archives Multiple Correct
- Archives Single Correct
- Archives Subjective
- Archives True/False
- Ex 4.1 (Objective)
- Ex 4.2 (Objective)
- Ex 4.3 (Objective)
- Ex 4.3 More Than One Correct
- Ex4.4 Objective
- Exercises Assertion-Reasoning
- Exercises Fill In The Blanks
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises True/False
- Illustration
- Solved Example