Complete Solutions to Illustrations of chapter GRAPHS OF TRIGONOMETRIC FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | GRAPHS OF TRIGONOMETRIC FUNCTIONS |
| CENGAGE NEW | Illustrations |
| Number Of Questions | 46 |
| Academic Year | 2023-24 |
Plot `y=sinxa n dy=sin2xdot`
02:30View SolutionPlot `y=sinxa n dy=sinx/2`
02:30View SolutionDraw the graph of `y=tan(3x)`.
02:09View SolutionDraw the graph of `y=sec^(2)x-tan^(2)x.` Is `f(x)` periodic? If yes, what is its fundamental period?
02:24View SolutionDraw the graph of `y=(tanx)/(tanx).` Is `f(x)` periodic? If yes, what is its fundamental period?
02:16View SolutionWhich of the following is highest?
`(a) " cosec " 1" "(b) " cosec " 2`
`( c ) " cosec " 4" "(d) " cosec " (-6)`
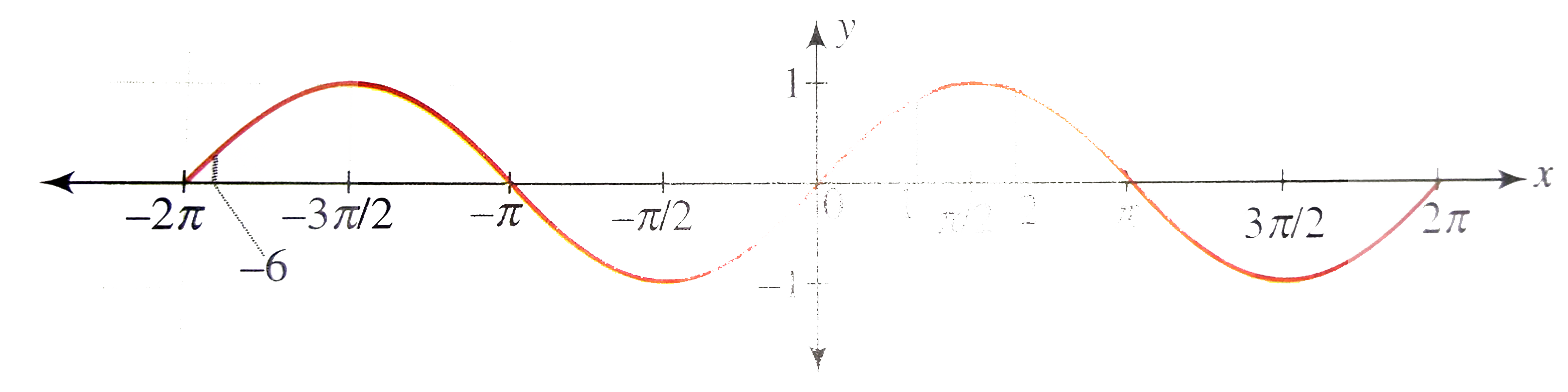 04:33View Solution
04:33View SolutionDraw the graph of the function `y=f(x)=lim_(ntooo) cos^(2n)x` and find its period.
03:10View SolutionFind the number of solution to the equation `x^(2)tanx=1,x in [0,2pi].`
01:19View SolutionSolve `tanx >cotx ,` where `x in [0,2pi]dot`
02:24View SolutionLet `f(x)=xsinpix ,\ x >0` . Then for all natural numbers `n ,\ f^(prime)(x)` vanishes at A unique point in the interval `(n ,\ n+1/2)` a unique point in the interval `(n+1/2,\ n+1)` a unique point in the interval `(n ,\ n+1)` two points in the interval `(n ,\ n+1)`
05:09View SolutionIf `0 lt alpha lt (pi)/(3)`, then prove that `alpha (sec alpha) lt (2pi)/(3).`
02:18View SolutionDraw the graph of `y = [sin x], x in [0, 2pi], ` where `[*]` represents the greatest integer function.
04:41View SolutionDraw the graph of `f(x) = [tan x], 0 le x le 5pi//12`, where `[*]` represents the greatest integer function.
05:03View SolutionDraw the graph of `f(x) = e^(sin x).`
04:06View SolutionDraw the graph of `y = sin 2^(x).`
03:20View SolutionDraw the graph of `y=(sin2x)sqrt(1+tan^2x)` , find its domain and range.
06:30View SolutionDraw the graph `y = sin^(2)x.`
02:03View SolutionDraw the graph of `y = sin^(3)x.`
03:05View SolutionDraw the graph of `f(x) = |sinx| + |cos x|, x in R`.
03:11View SolutionDraw the graph of `f(x) = sqrt(sin x)`.
02:36View SolutionDraw the graph of `y = (cos(|x| + (pi)/(2)))/(sin x).` Is the function periodic ?
02:28View SolutionDraw the graph of `f(x) = cos pi[x]`, where `[*]` represents the greatest integer function. Find the period of the function.
02:26View SolutionDraw the graph of `f(x) = sec x + "cosec " x, x in (0, 2pi) - {pi//2, pi, 3pi//2}`
Also find the values of 'a' for which the equation `sec x + "cosec " x = a` has two distinct root and four distinct roots.View SolutionDraw the graph of `f(x) = (sin x)/(sqrt(1 + tan^(2)x))- (cos x)/(sqrt(1 + cot^(2)x))`. Then find the range of f(x).
View SolutionFind the area bounded by the following curve :
(i) `f(x) = sinx, g(x) = sin^(2)x, 0 le x le 2pi`
(ii) `f(x) = sinx, g(x) = sin^(4)x, 0 le x le 2pi`View SolutionWrite the equivalent (piecewise) definition of `f(x)=sgn(sinx)dot`
03:36View SolutionDraw the graph of `f(x) = {sin x},` where `{*}` represents the fractional part function.
05:06View SolutionDraw a graph of `f(x) = sin {x}`, where `{x}` represents the greatest integer function.
View SolutionDraw the graph of `f(x) " maximum " {2 sin x, 1 - cos x}, x in (0, pi)`. Also find the range of `g(x) " min " {2 sin x, 1 - cos x}, x in (0, pi)`
View SolutionDraw the graph of `y = log_(e) (sin x).`
View SolutionDraw the graph of `[y] = sin x, x in [0,2pi]` where `[*]` denotes the greatest integer function
View SolutionDraw the graph of y = x sin x.
View SolutionDraw the graph of `y = e^(x) sin 2pix`.
View SolutionLet [x] denotes the greatest integer less than or equal to x. If `f(x) =[x sin pi x]`, then `f(x)` is
10:52View SolutionEvaluate : `[lim_(x to 0) (sin x)/(x)]`, where `[*]` represents the greatest integer function.
03:16View SolutionDiscuss maxima/minima of `f(x) = (x)/(1 + x tan x), x in (0, (pi)/(2))`
View SolutionFind the values of `a` if equation `1-cosx=(sqrt(3))/2|x|x a ,x in (0,pi),` has exactly one solution.
04:58View SolutionFind the number of solution to the equation `sin x = x^(2) + 2x + 1.`
View SolutionProve that `sinx+2xgeq(3x(x+1))/pi, AA x in [0,pi/2]` (Justify the inequality, if any used).
05:02View SolutionFind the ratio of the areas of two regions of the curve `C_(1) -= 4x^(2) + pi^(2)y^(2) = 4pi^(2)` divided by the curve `C_(2) -= y = -(sgn(x - (pi)/(2)))cos x` (where sgn (x) = signum (x)).
View SolutionSolve `tan x lt 2`.
02:08View SolutionSolve `sinx >-1/2or` find the domain of `f(x)=1/(sqrt(1+2sinx))`
04:20View SolutionSolve : `2 cos^(2)theta + sin theta le 2`, where `pi//2 le theta le 3pi//2.`
03:10View SolutionSolve `sintheta+sqrt(3)costhetageq1,-pi
04:22View SolutionLet `f(x) = {{:(x^(2) + 3x",", -1 le x lt 0),(-sin x",", 0 le x lt pi//2),(-1 - cos x",", (pi)/(2) le x le pi):}` . Draw the graph of the function and find the following
(a) Range of the function
(b) Point of inflection
(c) Point of local minima05:46View SolutionIf `
04:10View Solution
Illustrations questions and complete solutions for chapter GRAPHS OF TRIGONOMETRIC FUNCTIONS of CENGAGE MATHS (HINGLISH) of Class 12
