Complete Solutions to Linked Comprehension of chapter GEOMETRICAL OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GEOMETRICAL OPTICS |
| CENGAGE PHYSICS | Linked Comprehension |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
Consider a transparent hemispher `(n=2)` in front of which a small object is placed in air `(n=1)` as shown in figure.
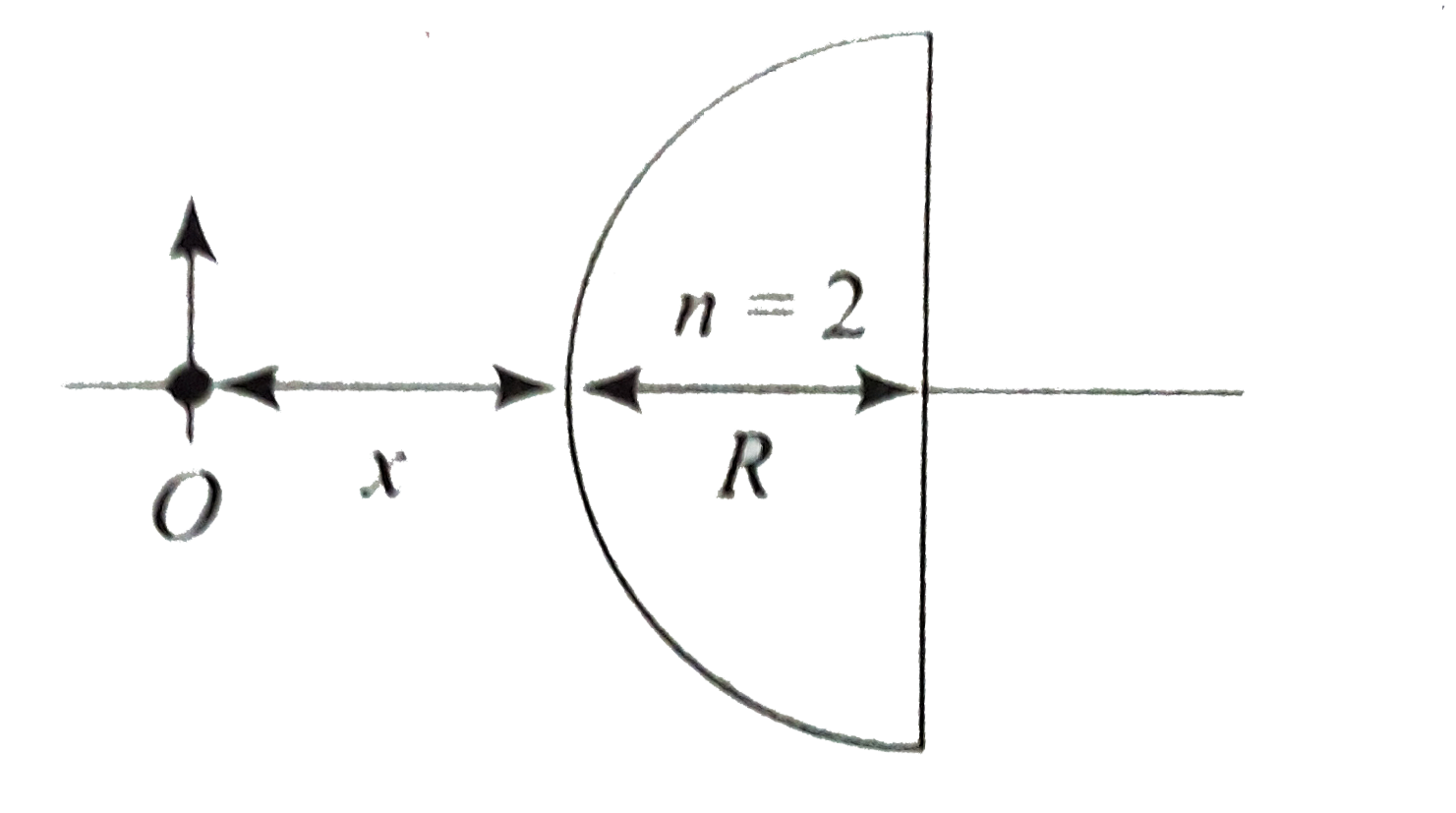
Q. Consider a ray starting from O which strikes the spherical surface at grazing incident `(i=90^(@))`. Takin `x=R`, what will be the angle (from normal) at which the ray may emerge from the plane surface.
View SolutionThis question concerna a symmetrical lens shown, along with its two focal points. It is made of plastice with `n=1.2` and has focal length f. Four different regions are shown:
Here,
A. `-oox lt -f` B. `-f lt x lt 0`
C. `0 lt x lt f` D. `f lt x lt oo`
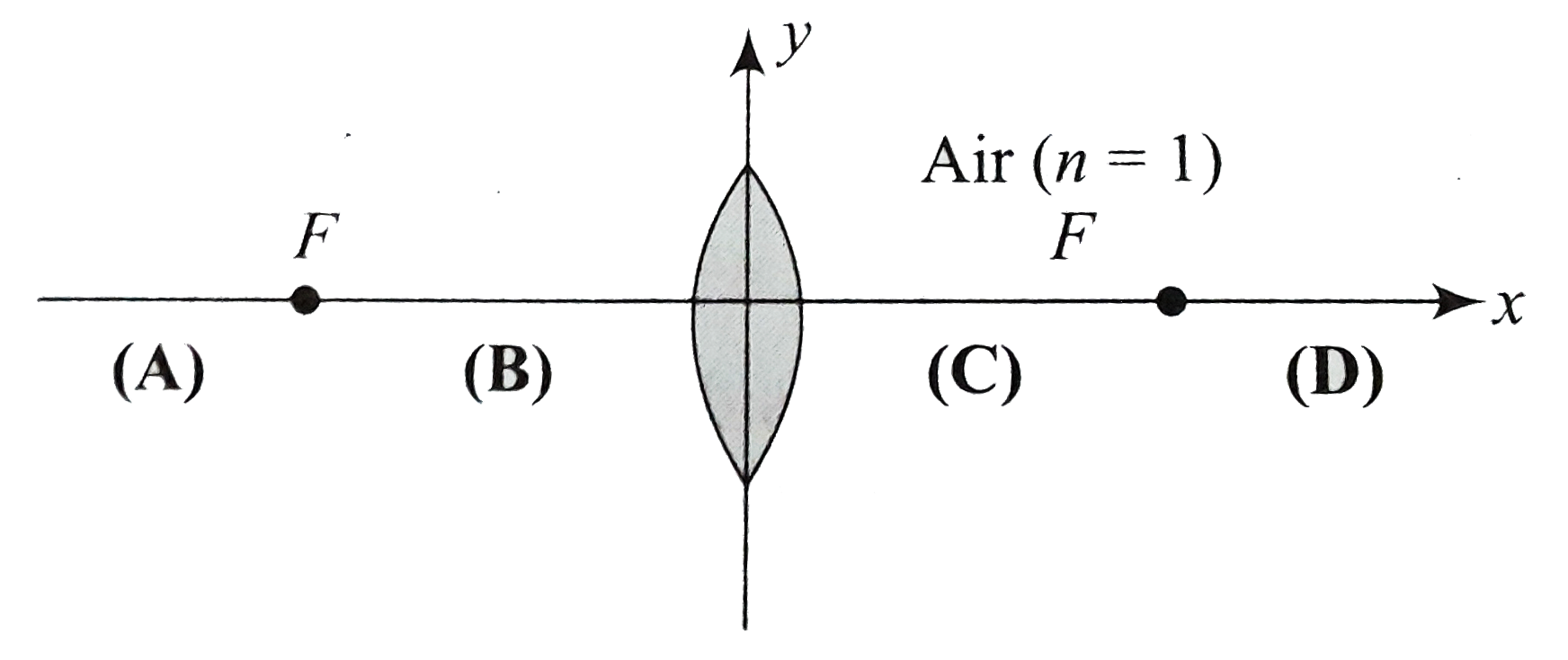
Q. If incident rays are converging, then in which region does the image appear?
View SolutionThis question concerna a symmetrical lens shown, along with its two focal points. It is made of plastice with `n=1.2` and has focal length f. Four different regions are shown:
Here,
A. `-oox lt -f` B. `-f lt x lt 0`
C. `0 lt x lt f` D. `f lt x lt oo`

Q. If incident rays are converging, then in which region does the image appear?
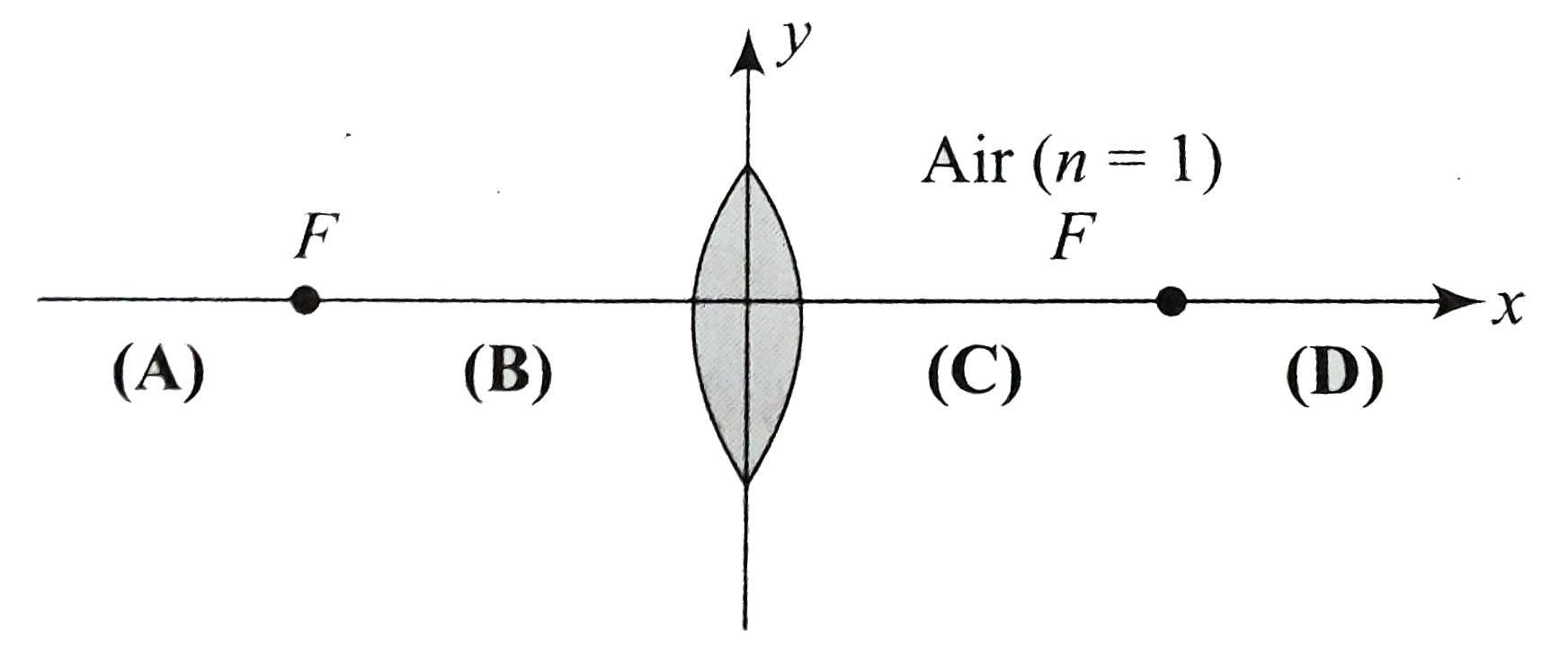
View SolutionThis question concerns a symmetrical lens shown, along with its two focal points. It is made of plastic with `n=1.2` and has focal length f. Four different regions are shown:
A. `-oo lt x lt -f`
B. `-f lt x lt 0`
C. `0 lt x lt f`
D. `f lt x lt oo`
A second lens is now placed adjacent to the first in contact with it. The new lens is concave, with a focal length `f=-3f`. In what region does the focal length of the two-lens system lie? Treat the lenses as thin.
View SolutionA point object O is placed in front of a concave mirror of focal length 10cm. A glass slab of refractive index `mu=3//2` and thickness 6cm is inserted between the object and mirror.

Q. Find the position and nature of the final image when the distance x shown in figure, is 5cm.
View SolutionA point object O is placed in front of a concave mirror of focal
length `10 cm`. A glass slab of refractive index `mu=3/2` and thickness `6cm` is
inserted between object and mirror. Find the position of final image when the
distance x shown in figure is

(a) `5cm` , (b) `20cm`
View SolutionA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.

Q. When viewer is ono left side of the hollow sphere, what will be the shift in position of the object?
View SolutionA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.
Q. When viewer is on right side of the hollow sphere, what will be apparent change in position of the object?

View SolutionA thin equiconvex lens of refractive index `3//2` is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index `4//3` . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. The radius of curvature of the convex surface is
View SolutionA thin biconvex lens of refractive index `3//2` is placed on a horizontal plane mirror as shown in Figure . The space between the lens and the mirror is then fille with water or refractive index `4//3`. It is found that when a point object is placed 15 cm above the lens on its principal axis, the object coincides with its own image. On representing with another liquid, the object and the image again coincide at a distance 25 cm from the lens. Calculate the refractive index of the liquid.

View Solution
A point object is placed at a distance of 0.3 m from a convex lens (focal length 0.2 m) cut into two halves each of which is displaced by 0.0005 m as shown in the figure. Find the position of the image . If more than one image is formed find their number and the distance between them.
View Solution
A point object is placed at a distance of 0.3 m from a convex lens (focal length 0.2 m) cut into two halves each of which is displaced by 0.0005 m as shown in the figure. Find the position of the image . If more than one image is formed find their number and the distance between them.
View Solution
A point object is placed at a distance of 0.3 m from a convex lens (focal length 0.2 m) cut into two halves each of which is displaced by 0.0005 m as shown in the figure. Find the position of the image . If more than one image is formed find their number and the distance between them.
View SolutionThe convex surface of a thin concave-convex lens of glass of refractive index 1.5 has a radius of curvature 20 cm. The concave surface has a radius of curvature 60 cm. The convex side is silvered and placed on a horizontal surface as shown in figure. (a) Where should a pin be placed on the axis so that its image is formed at the same place ? (b) If the concave part is filled with water (mu = 4/3), find the distance through which the pin should be moved so that the image of the pin again coincides with the pin.

View SolutionThe convex surface of a thin concave-convex lens of glass of refractive index 1.5 has a radius of curvature 20 cm. The concave surface has a radius of curvature 60 cm. The convex side is silvered and placed on a horizontal surface as shown in figure. (a) Where should a pin be placed on the axis so that its image is formed at the same place ? (b) If the concave part is filled with water (mu = 4/3), find the distance through which the pin should be moved so that the image of the pin again coincides with the pin.

View SolutionTwo thin convex lenses of focal lengths `f_(1)` and `f_(2)` are separated by a horizontal distance d (where`dltf_(1)`,`dltf_(2)`) and their centres are displaced by a vertical separation `triangle` as shown in the fig.
Taking the origin of coordinates O, at the centre of the first lens the x and y coordinates of the focal point of this lens system, for a parallel beam of rays coming form the left, are given by: `
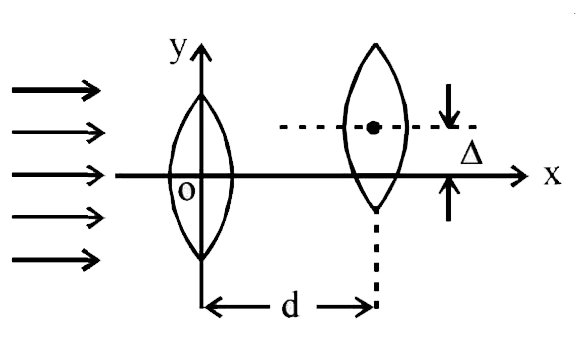
View SolutionTwo thin convex lenses of focal lengths `f_(1)` and `f_(2)` are separated by a horizontal distance d (where`dltf_(1)`,`dltf_(2)`) and their centres are displaced by a vertical separation `triangle` as shown in the fig.
Taking the origin of coordinates O, at the centre of the first lens the x and y coordinates of the focal point of this lens system, for a parallel beam of rays coming form the left, are given by: `
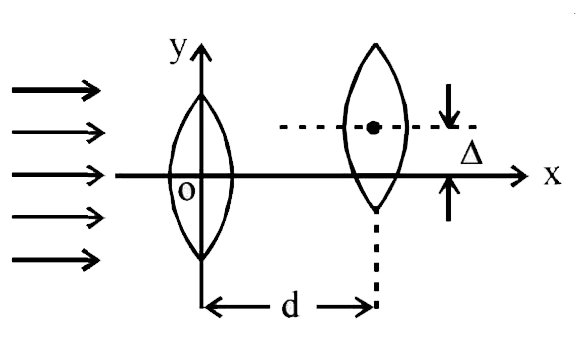
View SolutionA parallel beam of light falls successively on a thin convex lens of focal length 40 cm and then ono a thin convex lens of focal length 10cm as shown in figure.
In figure, the second lens is an equi-concave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm.
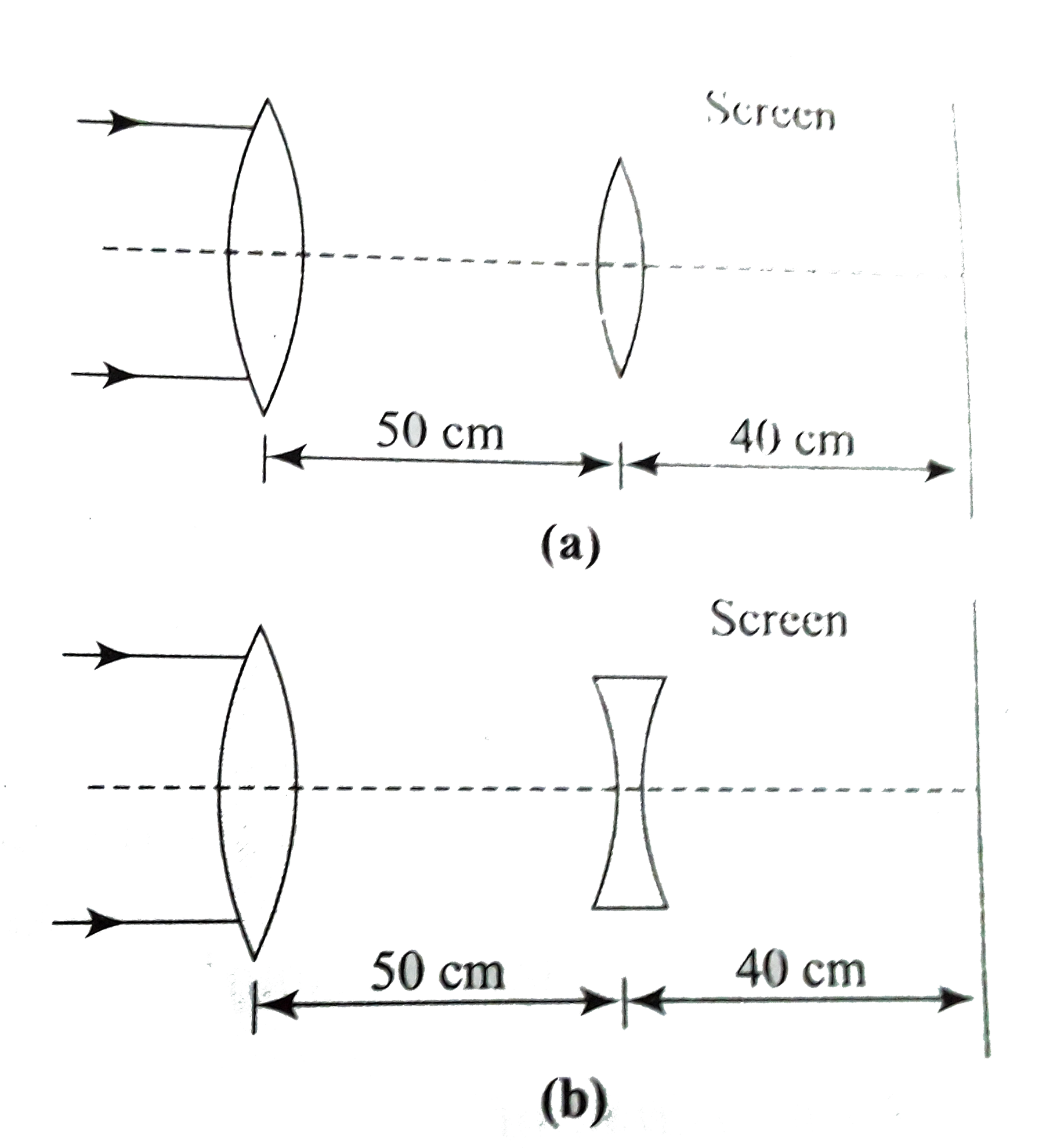
Q. Compare the area illuminated by the beam of light on the screen, which passes through the second lens in the two cases. The ratio `(A_(2)//A_(1))` will be
View SolutionA parallel beam of light falls successively on a thin convex lens of focal length 40 cm and then ono a thini convex lens of focal length 10cm as shown in figure.
In figure, the second lens is an equiconcave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm.
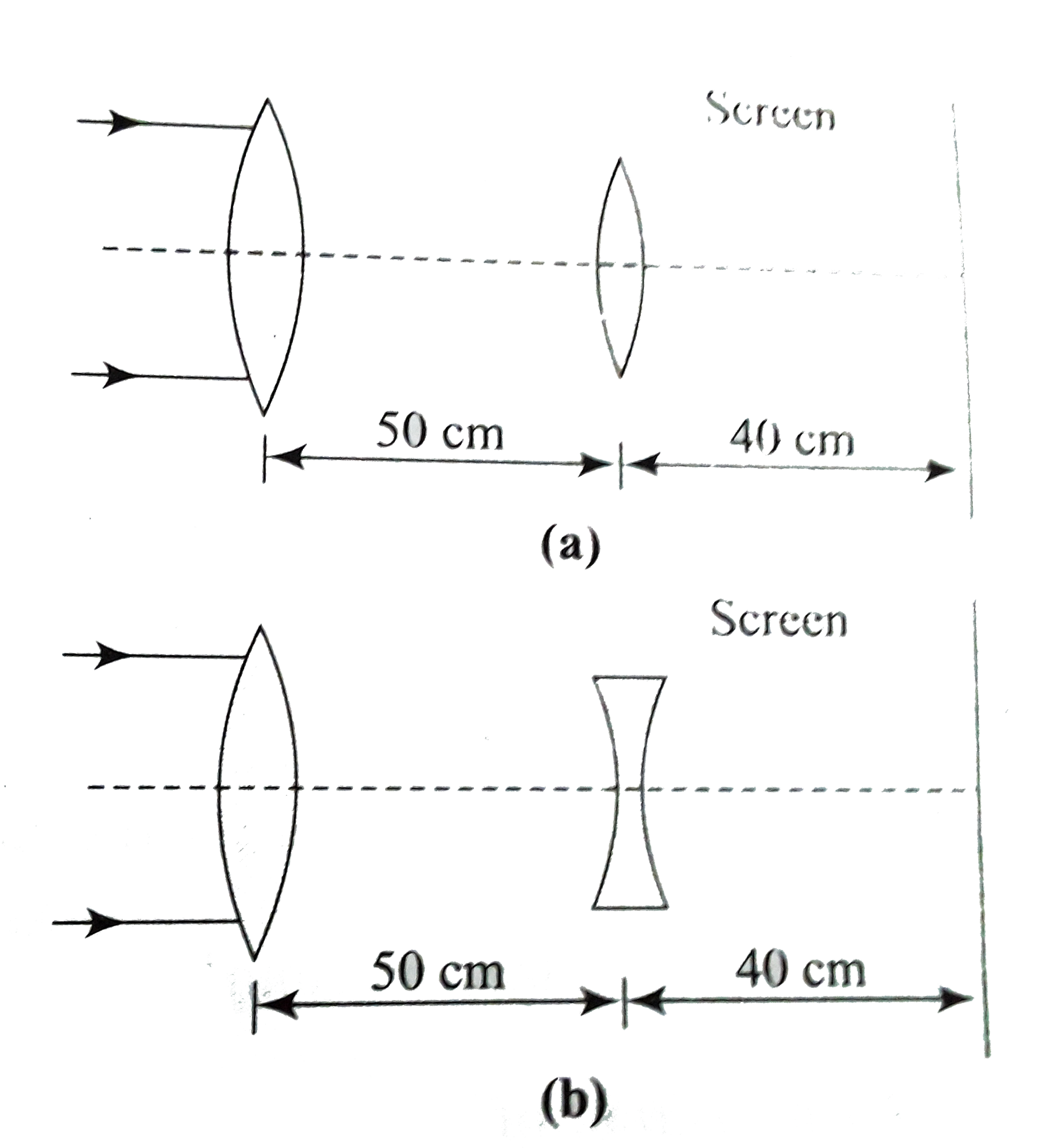
Q. Now, a liquid of refractive index `mu` is filled to the right of the second lens in case B such that the area illuminated in both the cases is the same. Determing the refractive index of the liquid.
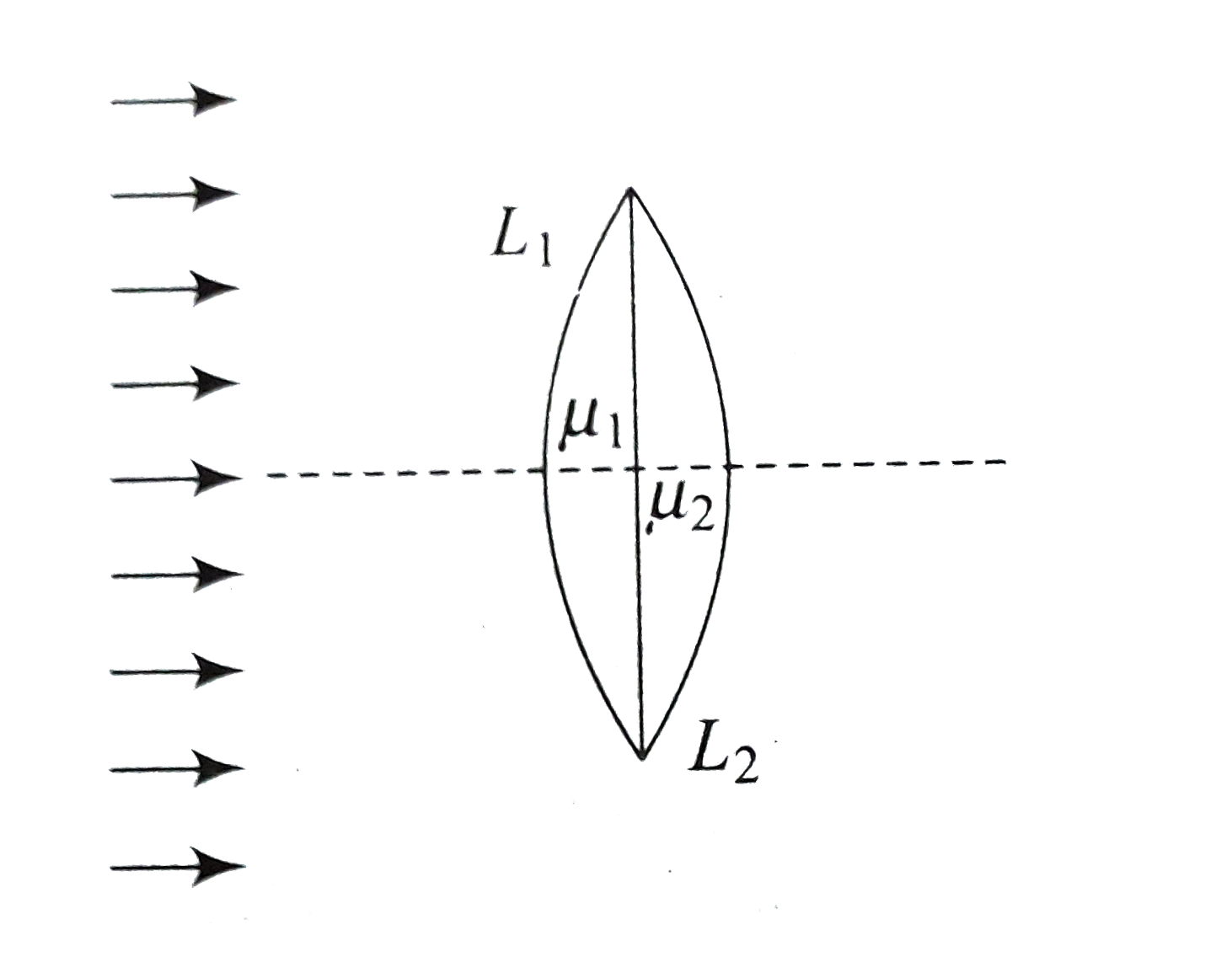
View SolutionTwo identical plano-convex lenses `L_(1)(mu_(1)-1.4)` and `L_(2)(mu_(2)-1.5)`
of radii of curvature `R=20cm` are placed as shown in Figure.
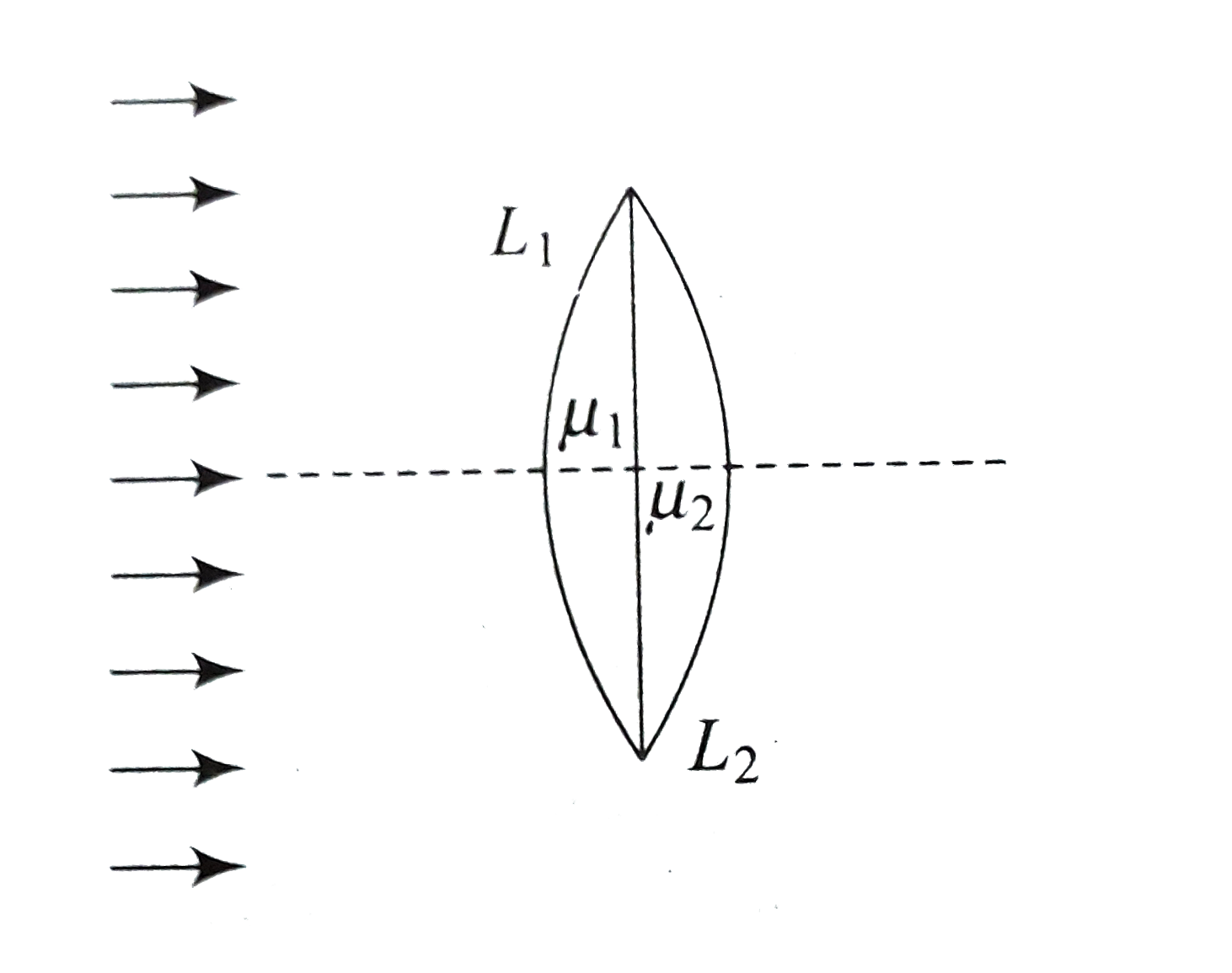
Q. Find the position of the image of the parallel beam of light relative to the common principal axis.
View SolutionTwo identical plano-convex lenses `L_(1)(mu_(1)-1.4)` and `L_(2)(mu_(2)-1.5)` of radii of curvature `R=20cm` are placed as shown in Figure.
Q. Now, the secocnd lens is shifted vertically downward by a small distance 4.5mm and the extended parts of `L_(1)` and `L_(2)` are blackened as shown in figure. Find the new position of the image of the parallel beam.
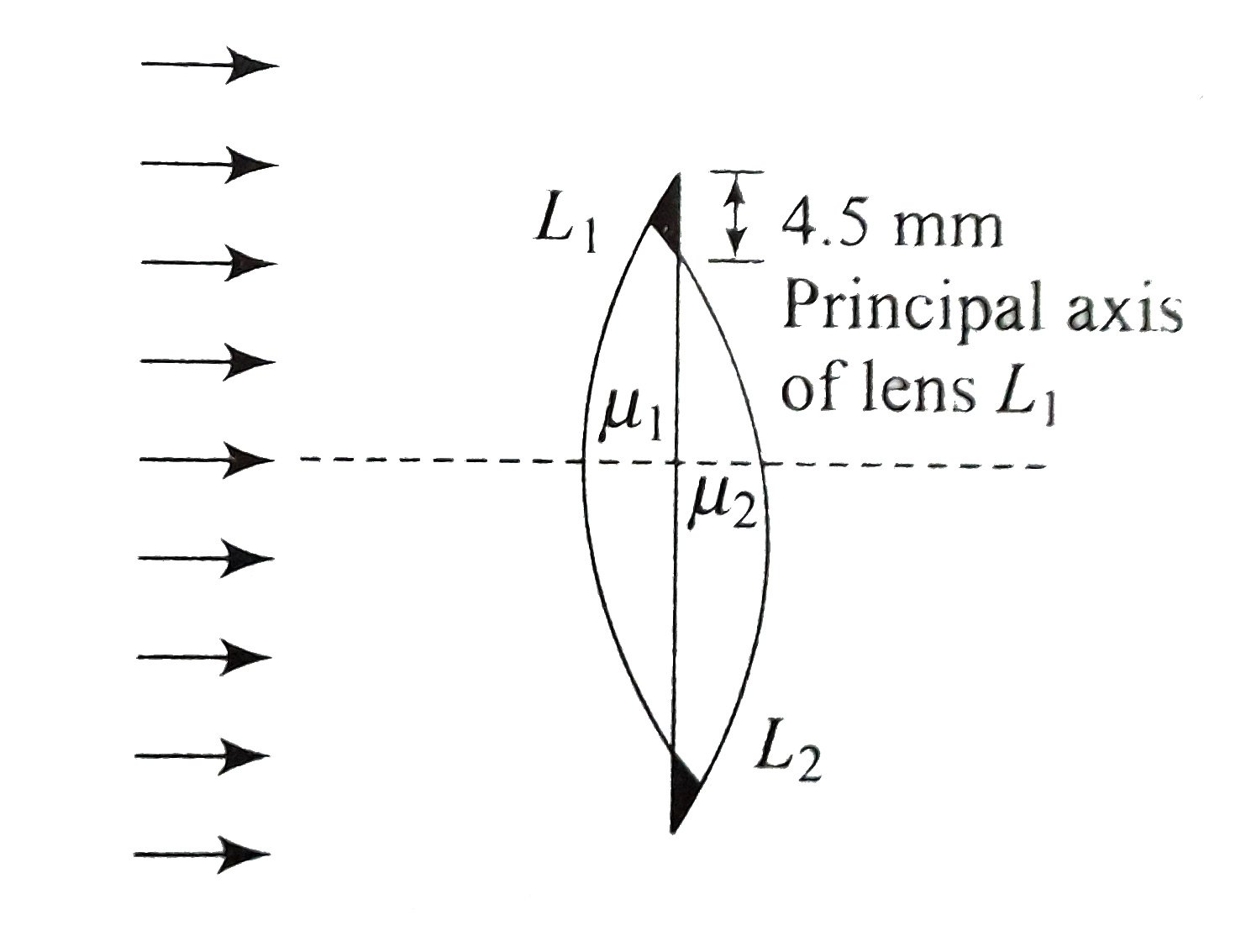
View SolutionA beam of light converges towards a point O, behind a convex mirror of focal length 20cm.
Q. Find the magnification and nature of the image when point O is 10cm behind the mirror.
View SolutionA beam of light converges towards a point O, behind a convex mirror of focal length 20cm.
Q. Similarly, as in above question when point O is 30cm behind the mirror.
View SolutionA ray of light enters a spherical drop of water of refractive index `mu` as shown in figure.
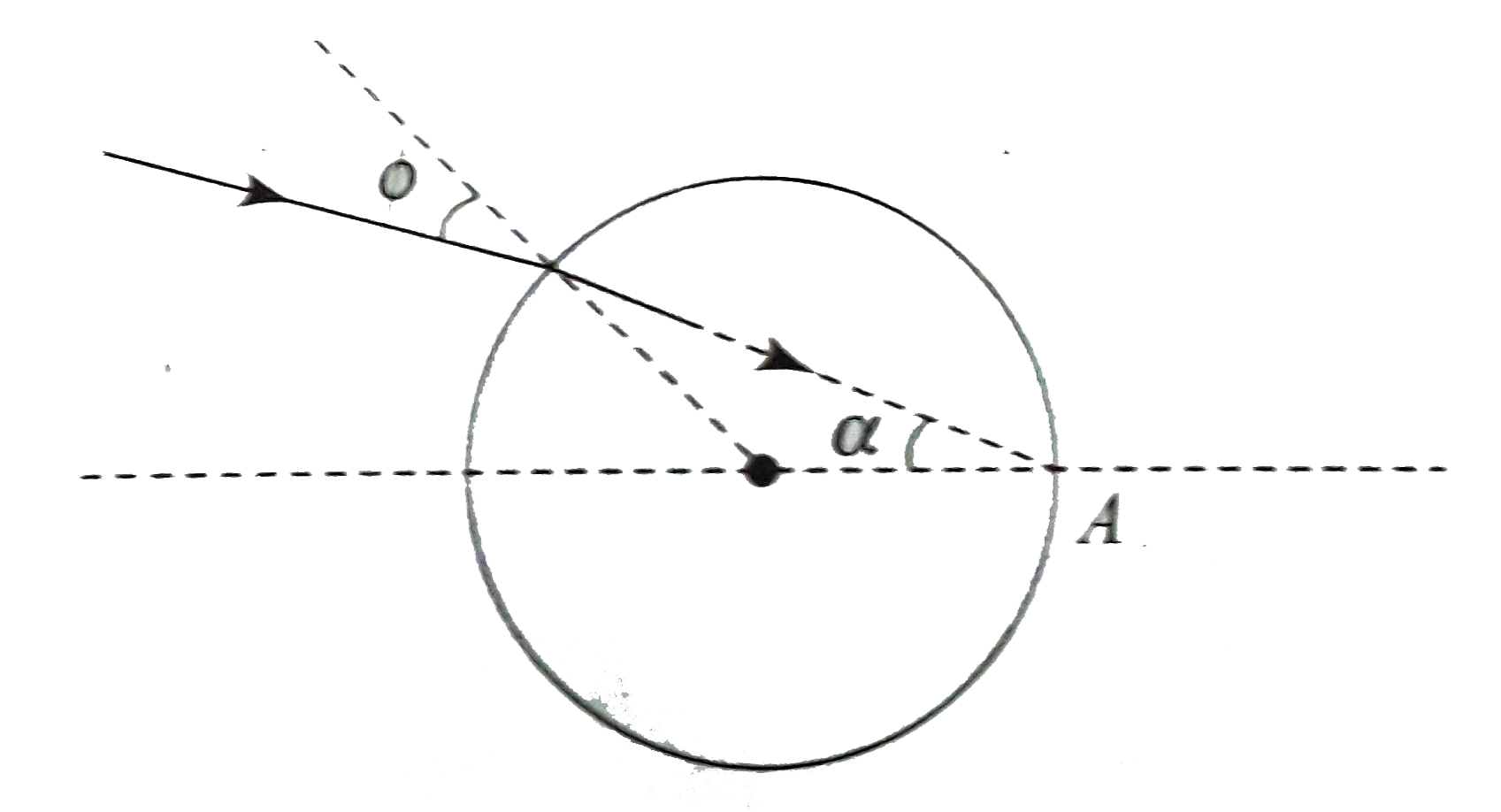
Q. Select the correct statement:
View SolutionA ray of light enters a spherical drop of water of refractive index `mu` as shown in figure.
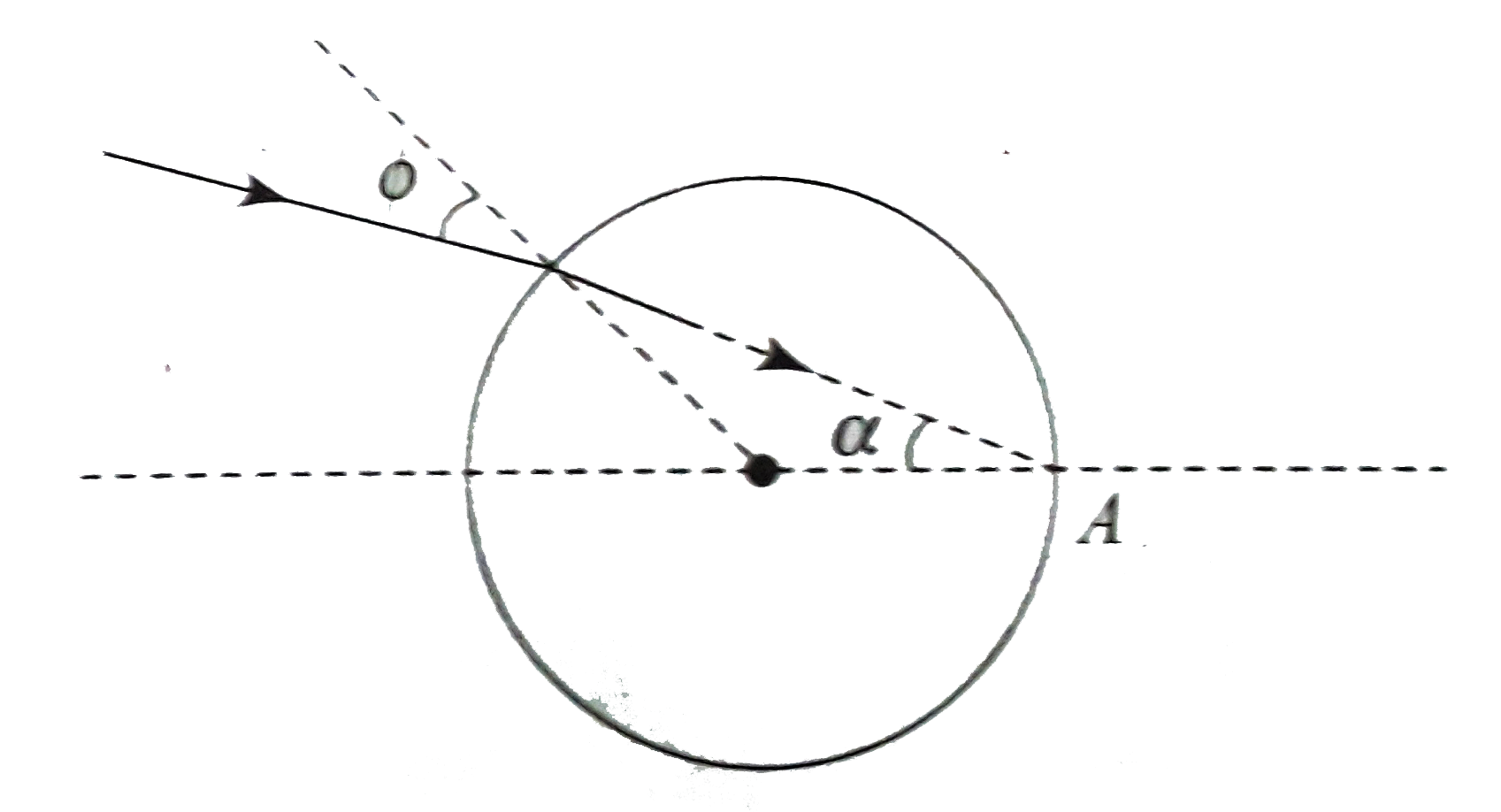
Q. An expression of the angle between incident ray and emergent ray (angle of deviation) as shown in figure.

View SolutionA ray of light enters a spherical drop of water of refractive index `mu` as shown in figure.
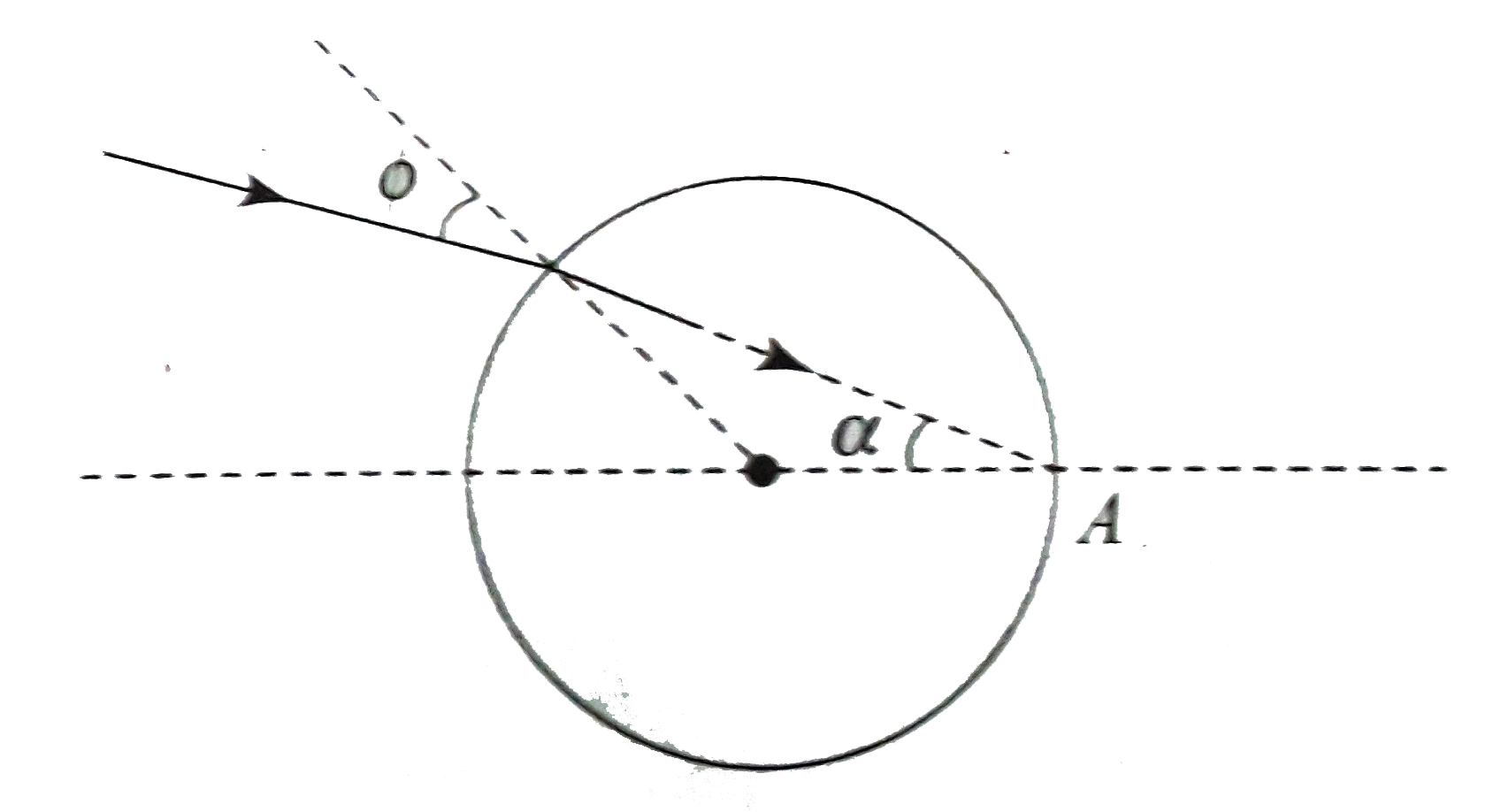
Q. Considert eh figure of question 60, the angle `phi` for which minimum deviation is produced will be given by
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is `+3D` (converging lens of focal length `100//3cm` ), then number of lens will be `+3`.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
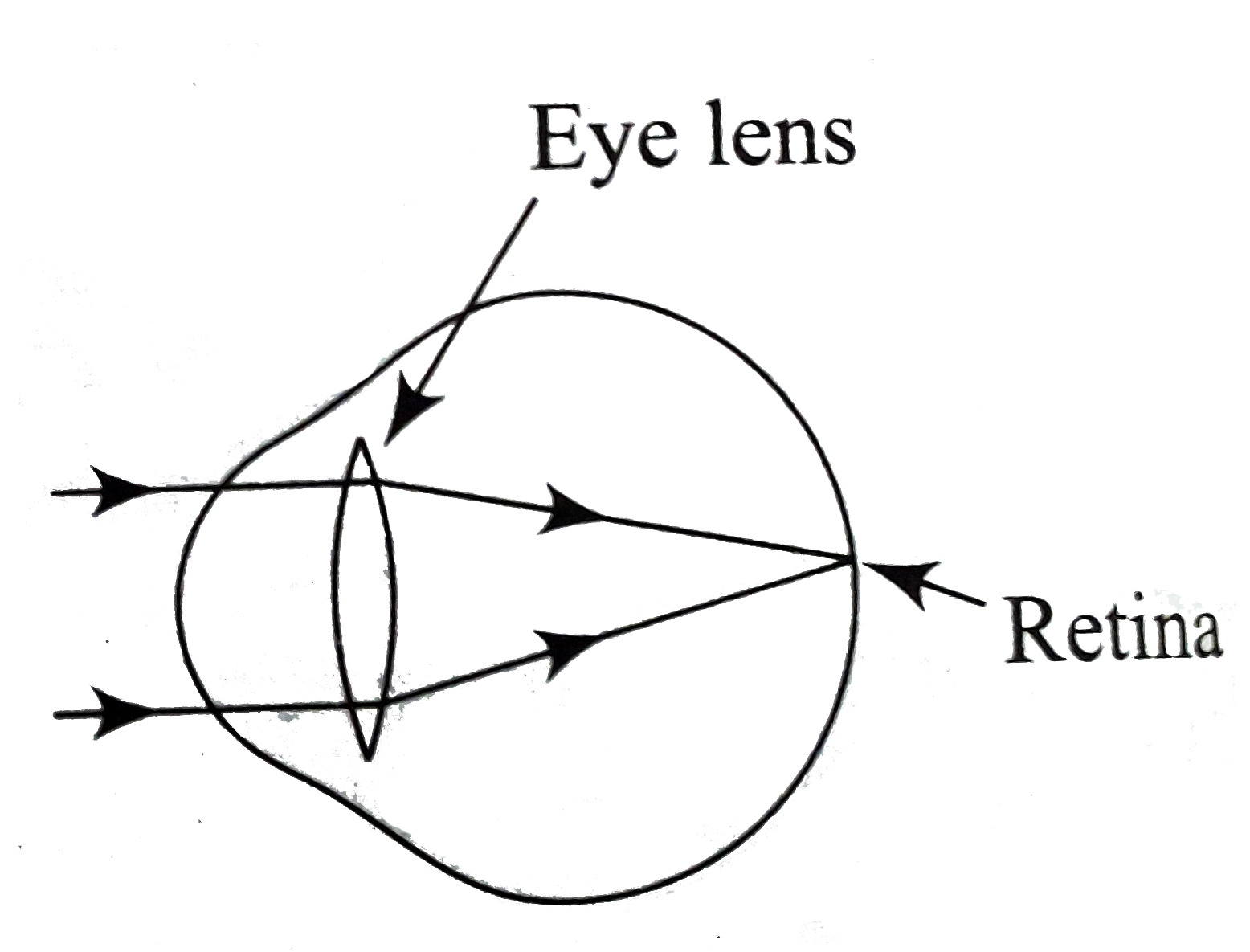
Q. Minimum focal length of eye lens of a normal peson is
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is `+3D` (converging lens of focal length `100//3cm` ), then number of lens will be `+3`.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
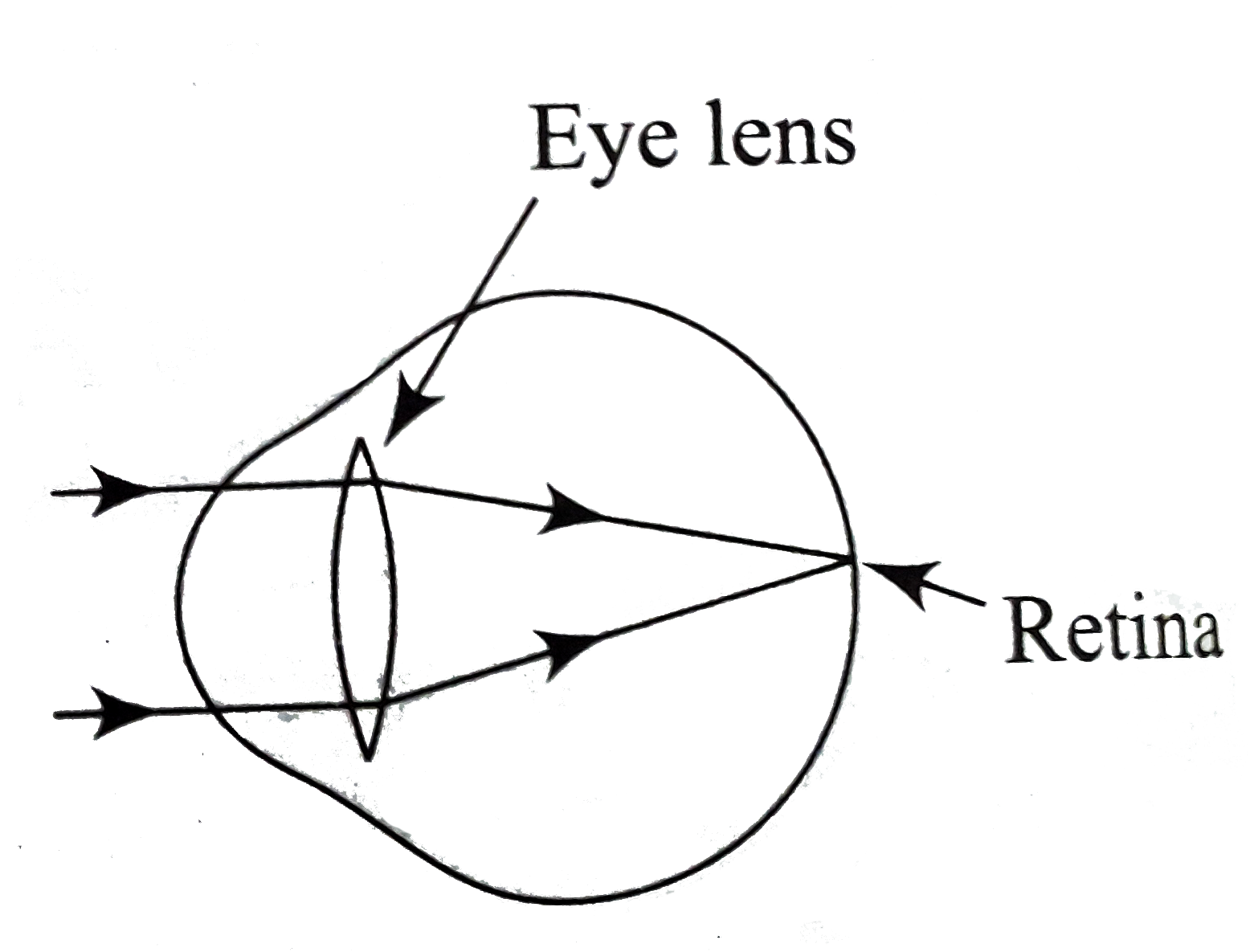
Q. Maximum focal length of a eye lens of a normal person is
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is `+3D` (converging lens of focal length `100//3cm` ), then number of lens will be `+3`.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
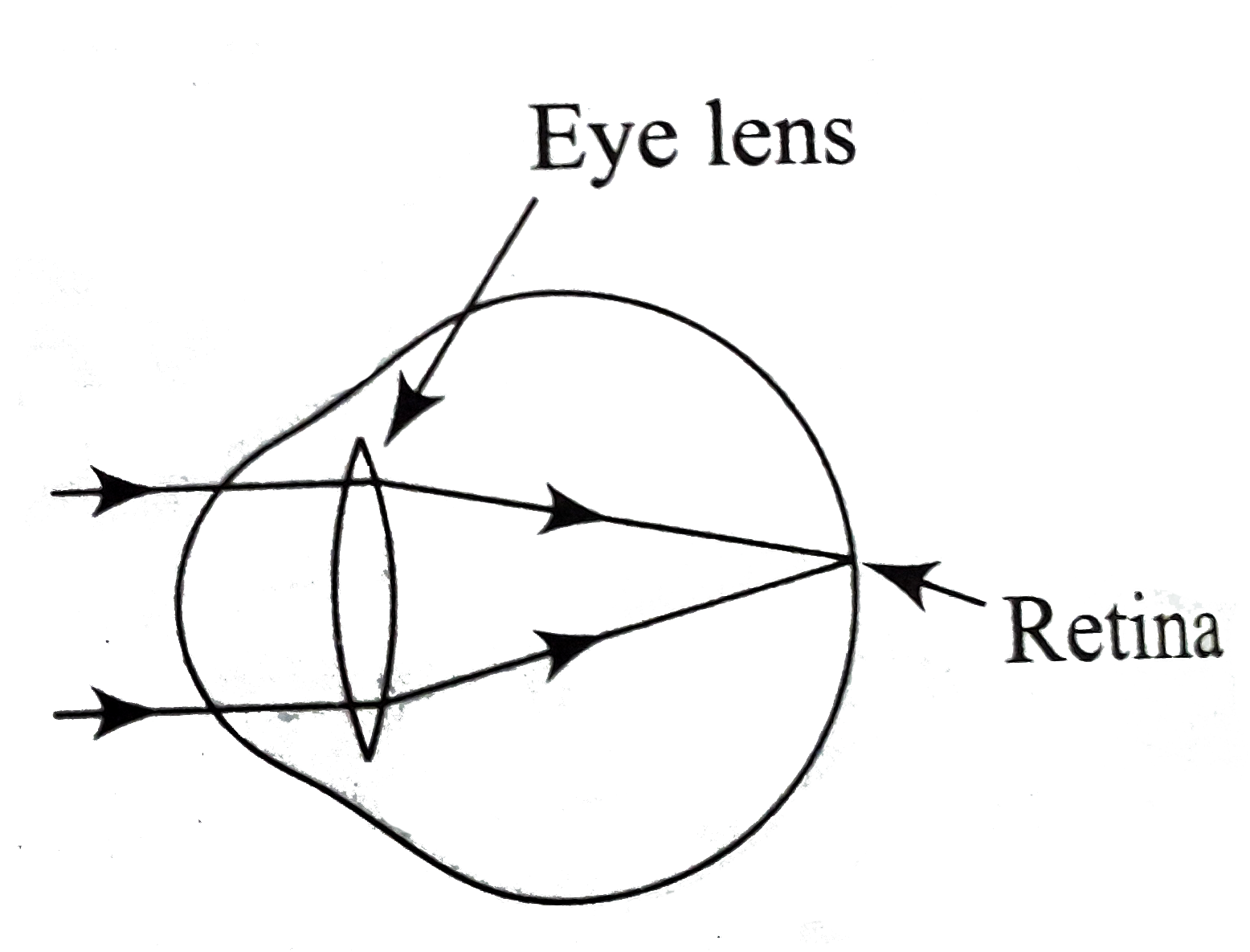
Q. A near sighted man can clearly see ojects only upto a distance of 100cm and not beyond this. The number of the spectacle lenses necessary for the remedy of this defect will be
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is `+3D` (converging lens of focal length `100//3cm` ), then number of lens will be `+3`.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
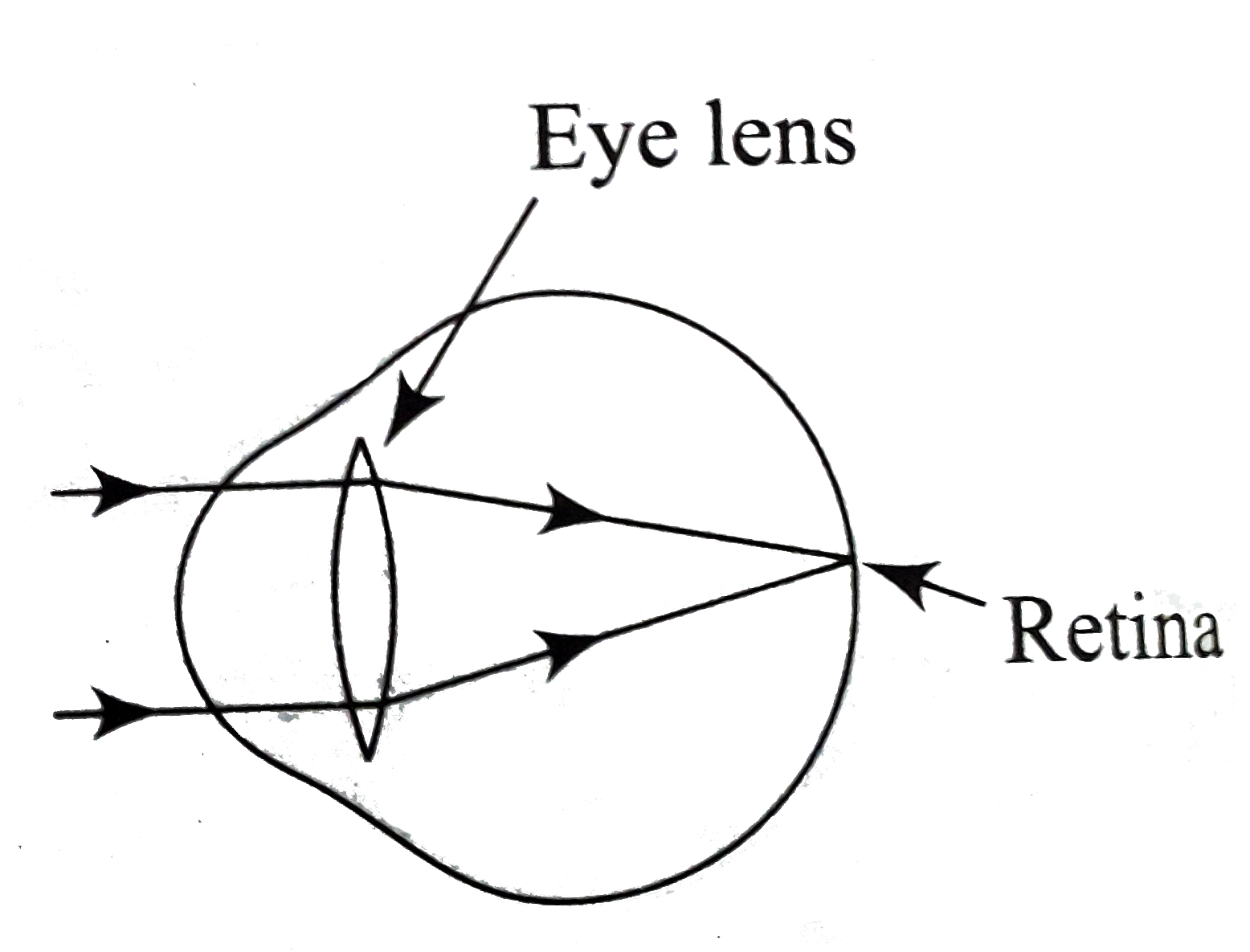
Q. A far sighted man connot see objects clearly unless they are at least 100cm from his eyes. The number of the spectacle lenses that will make his range of clear vision equal to an average grown up person will be
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is `+3D` (converging lens of focal length `100//3cm` ), then number of lens will be `+3`.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
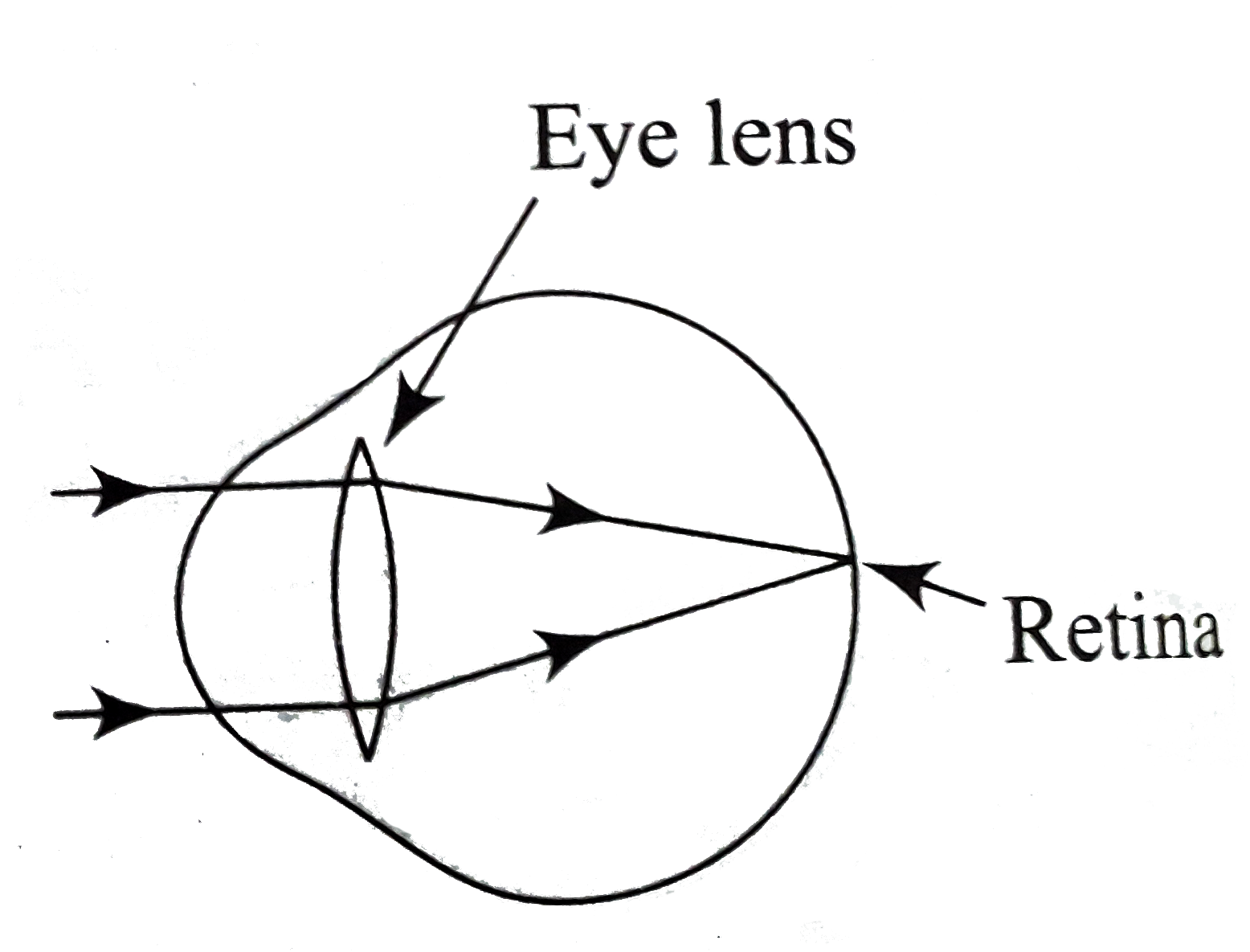
Q. A person can see objects clearly from distance 10cm to `oo`. Then, we can say that the person is
View SolutionA parallel beam of light falls on a solid tranparent sphere.
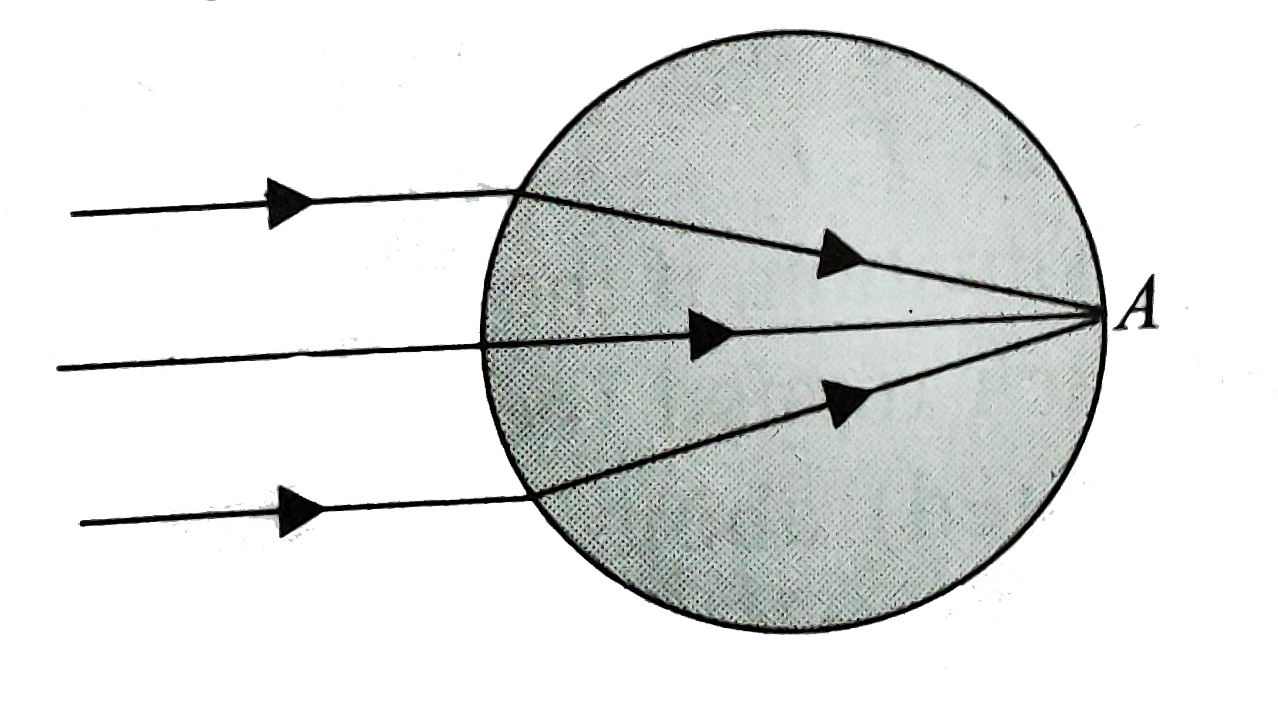
Q. Which is corret?
View SolutionA parallel beam of light falls on a solid tranparent sphere.
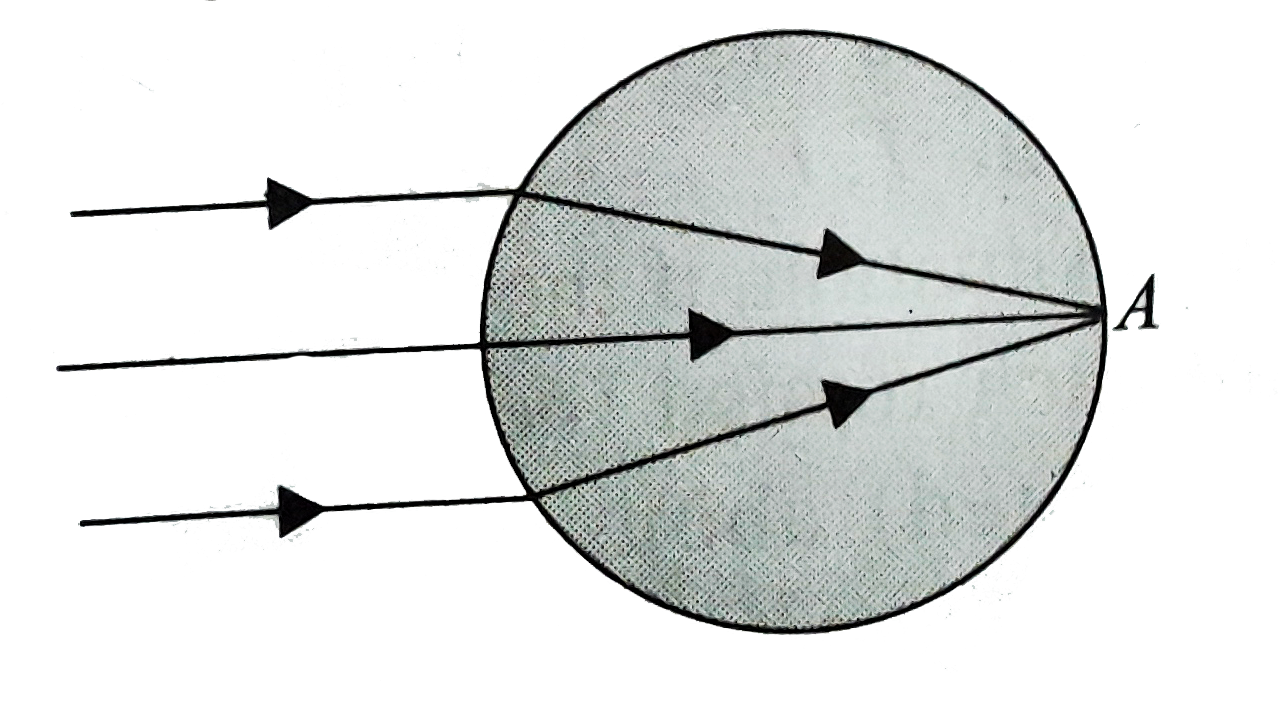
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionA parallel beam of light falls on a solid tranparent sphere.

Q. For what value of refractive index `mu`, the thin beam can be focussed at centre of sphere.
View SolutionPulfrich refractometer is used to measure the refractive index of solids and liquid. It consist of right angled prism. A having its two faces perfectly plane. One of the face is horizontal and the other is vertical as shown is figure. The solid B whose refractive index is to be determined is taken having two faces cut perpendicular to one another. Light is incident in a direction parallel to the horizontal surface so that the light entering the prism A is at critical angle C. Finally, it emerges from the prism at an angle i. Let the refractive index of the solid be `mu` and that of the prism A be `mu_(0)` (which is known). Here `mu_(0)gtmu` and by measuring i, `mu` can be determinged.
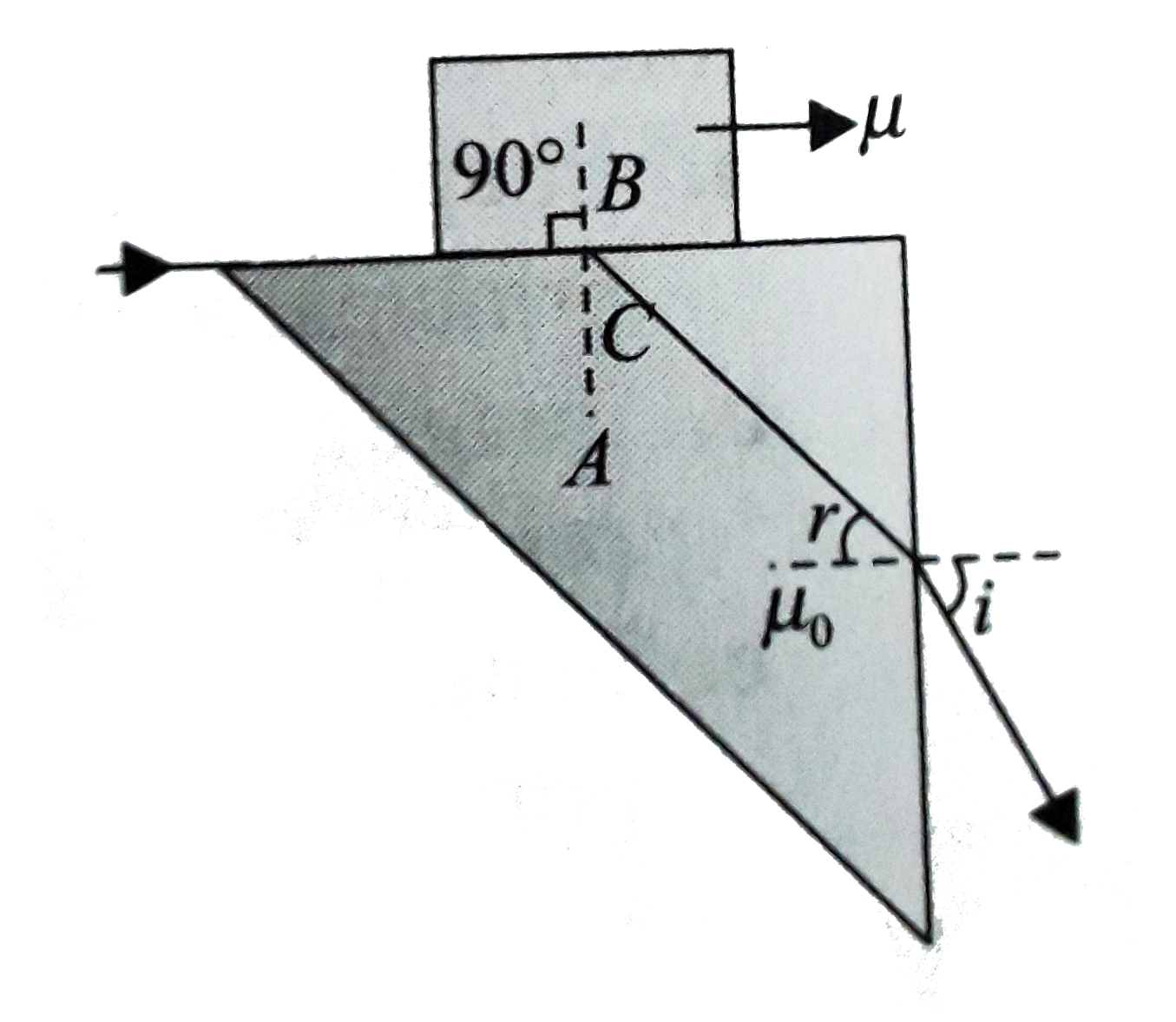
Q. Refractive index of the solid `(mu)` in terms of `mu_(0)` and i is
View SolutionPulfrich refractometer is used to measure the refractive index of solids and liquid. It consist of right angled prism. A having its two faces perfectly plane. One of the face is horizontal and the other is vertical as shown is figure. The solid B whose refractive index is to be determined is taken having two faces cut perpendicular to one another. Light is incident in a direction parallel to the horizontal surface so that the light entering the prism A is at critical angle C. Finally, it emerges from the prism at an angle i. Let the refractive index of the solid be `mu` and that of the prism A be `mu_(0)` (which is known). Here `mu_(0)gtmu` and by measuring i, `mu` can be determinged.

Q. Refractive index of the solid `(mu)` in terms of `mu_(0)` and i is
View SolutionPulfrich refractometer is used to measure the refractive index of solids and liquid. It consist of right angled prism. A having its two faces perfectly plane. One of the face is horizontal and the other is vertical as shown is figure. The solid B whose refractive index is to be determined is taken having two faces cut perpendicular to one another. Light is incident in a direction parallel to the horizontal surface so that the light entering the prism A is at critical angle C. Finally, it emerges from the prism at an angle i. Let the refractive index of the solid be `mu` and that of the prism A be `mu_(0)` (which is known). Here `mu_(0)gtmu` and by measuring i, `mu` can be determinged.

Q. Refractive index of the solid `(mu)` in terms of `mu_(0)` and i is
View SolutionAn object is present on the principal axis of a concave mirror at a distance 30cm from it. Focal length of mirror is 20cm.
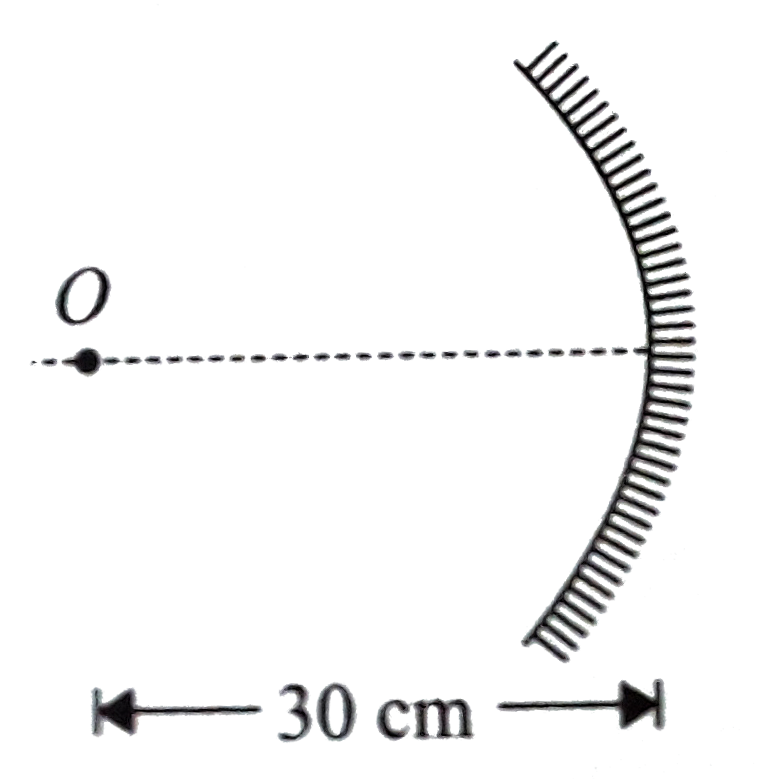
Q. Image formed by mirror is
View SolutionAn object is placed between a plane mirror and a concave mirror of focal length 15 cm as shown in Figure . Find the position of the images after two reflections.

View SolutionAn object is present on the principal axis of a concave mirror at a distance 30cm from it. Focal length of mirror is 20cm.
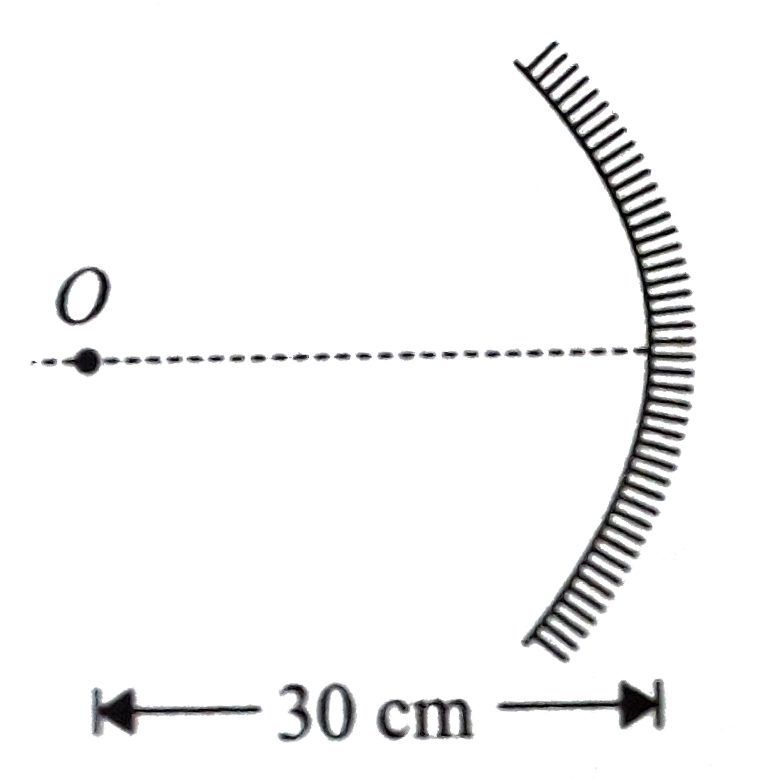
Q. If object starts moving with `2cms^(-1)` perpendicular to principal axis above the principal axis then,
View SolutionAn object kept near a convex lens of focal length f, executes SHM between P and Q according to the equation `y=A sinomegat`, O being the mean position. Take x-axis as the principal axis of the lens and `A lt lt D` to answer the following questions:
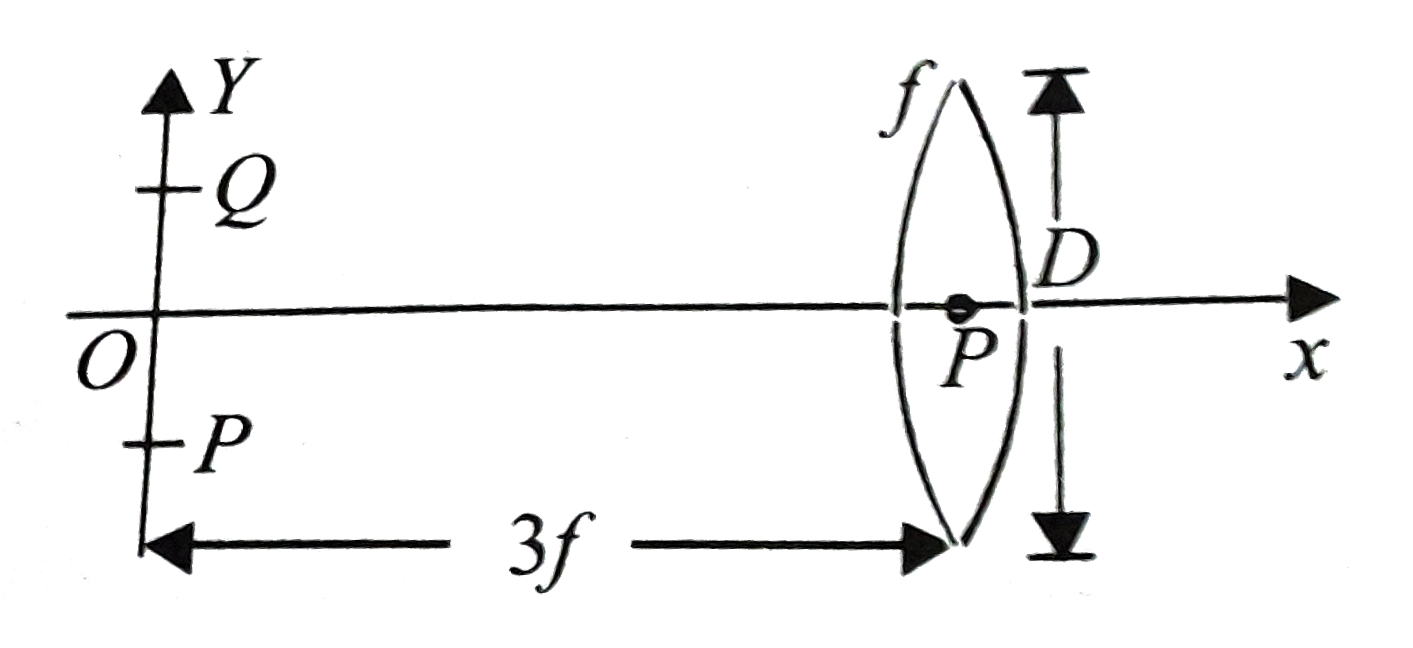
Q. The phase difference between the object and the image oscillations is
View SolutionAn object kept near a convex lens of focal length f, executes SHM between P and Q according to the equation `y=A sinomegat`, O being the mean position. Take x-axis as the principal axis of the lens and `A lt lt D` to answer the following questions:
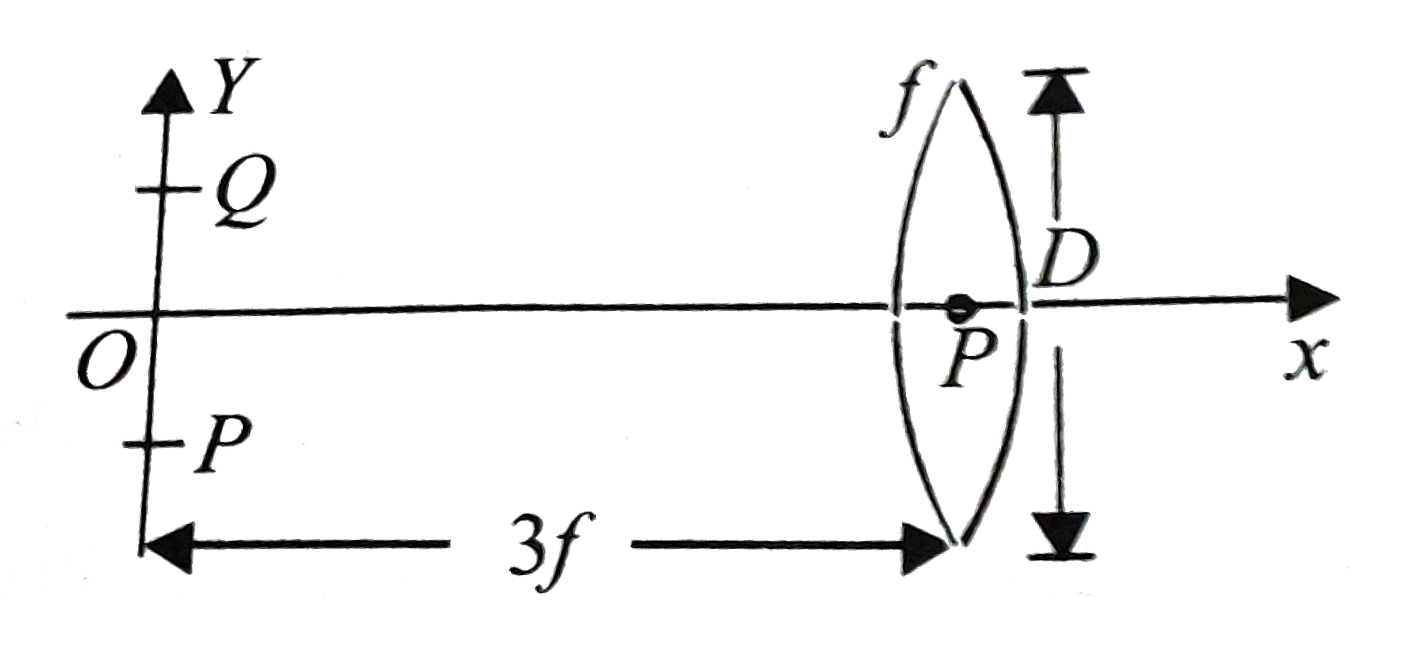
Q. The amplitude of oscillation of the image is
View SolutionAn object kept near a convex lens of focal length f, executes SHM between P and Q according to the equation `y=A sinomegat`, O being the mean position. Take x-axis as the principal axis of the lens and `A lt lt D` to answer the following questions:
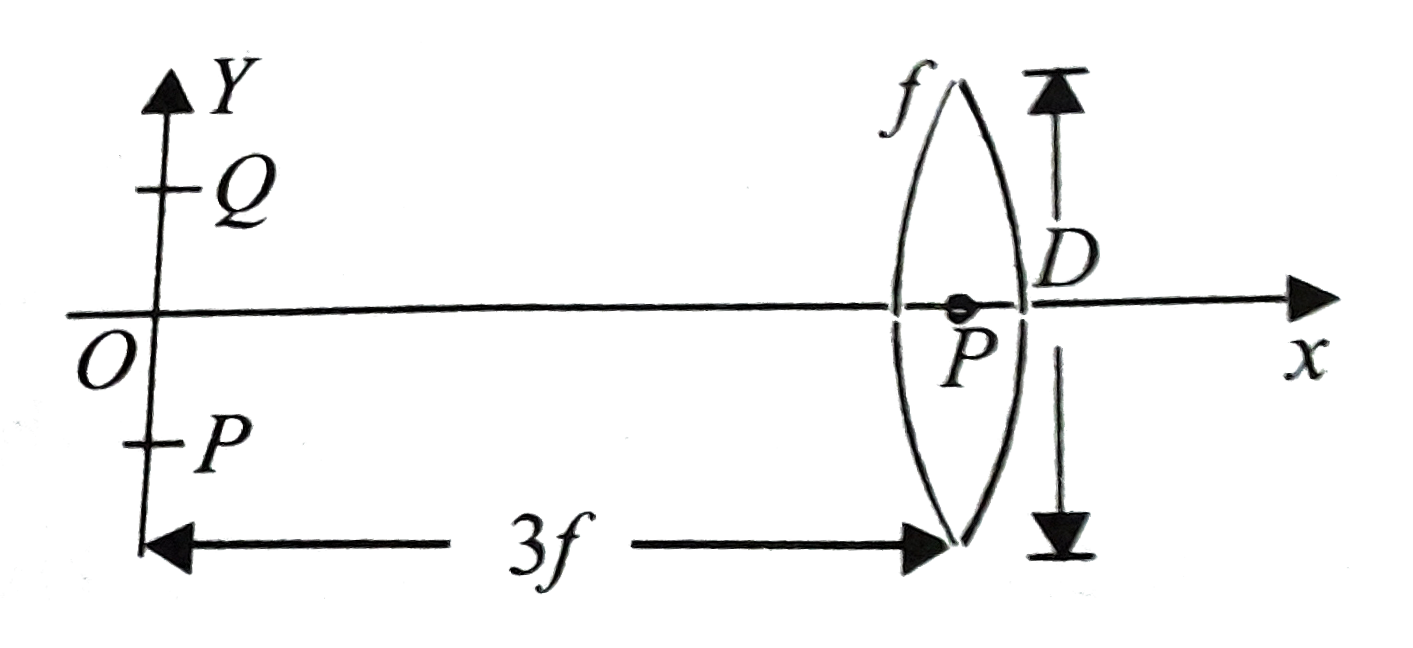
Q. The velocity of the image when the object crosses the mean position and goes toward Q is
View SolutionA convex lens of focal length 40cm is held at a distance 12cm coaxially above a concave mirror of focale length 18cm.
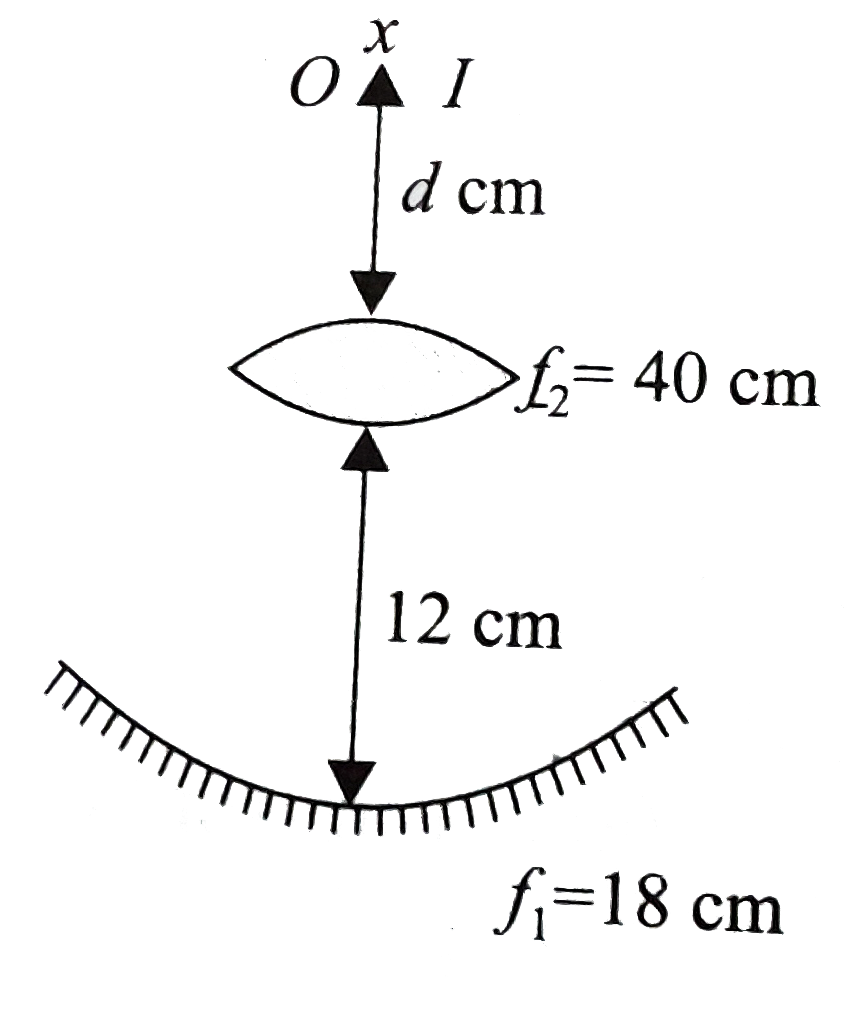
Q. A luminous point object placed d cm above the lens on its axis gives rise to an imag coincident iwth itself, then the value of d is equal to
View SolutionA convex lens of focal length 40cm is held at a distance 12cm coaxially above a concave mirror of focale length 18cm.
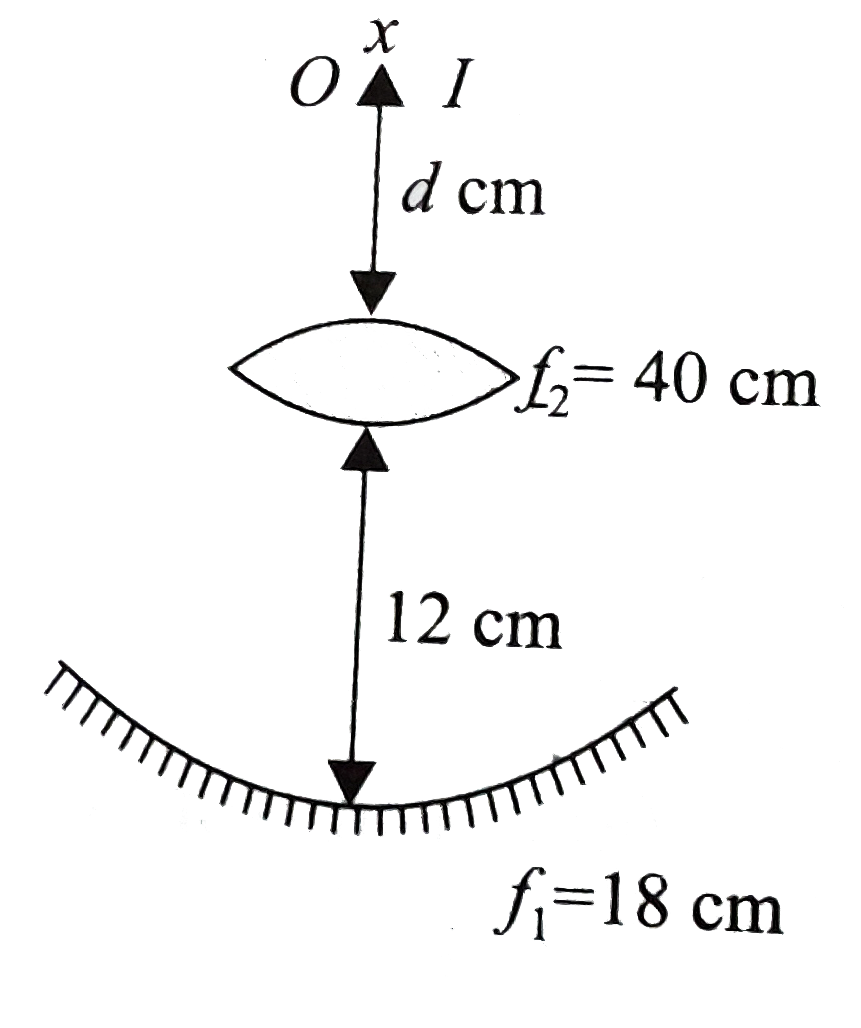
Q. If the convex lens is replaced by a glass plate of thickness 6cm, refractive index `mu=(3)/(2)` and gives rise to an image coincident with itself, then the value of d is equal to
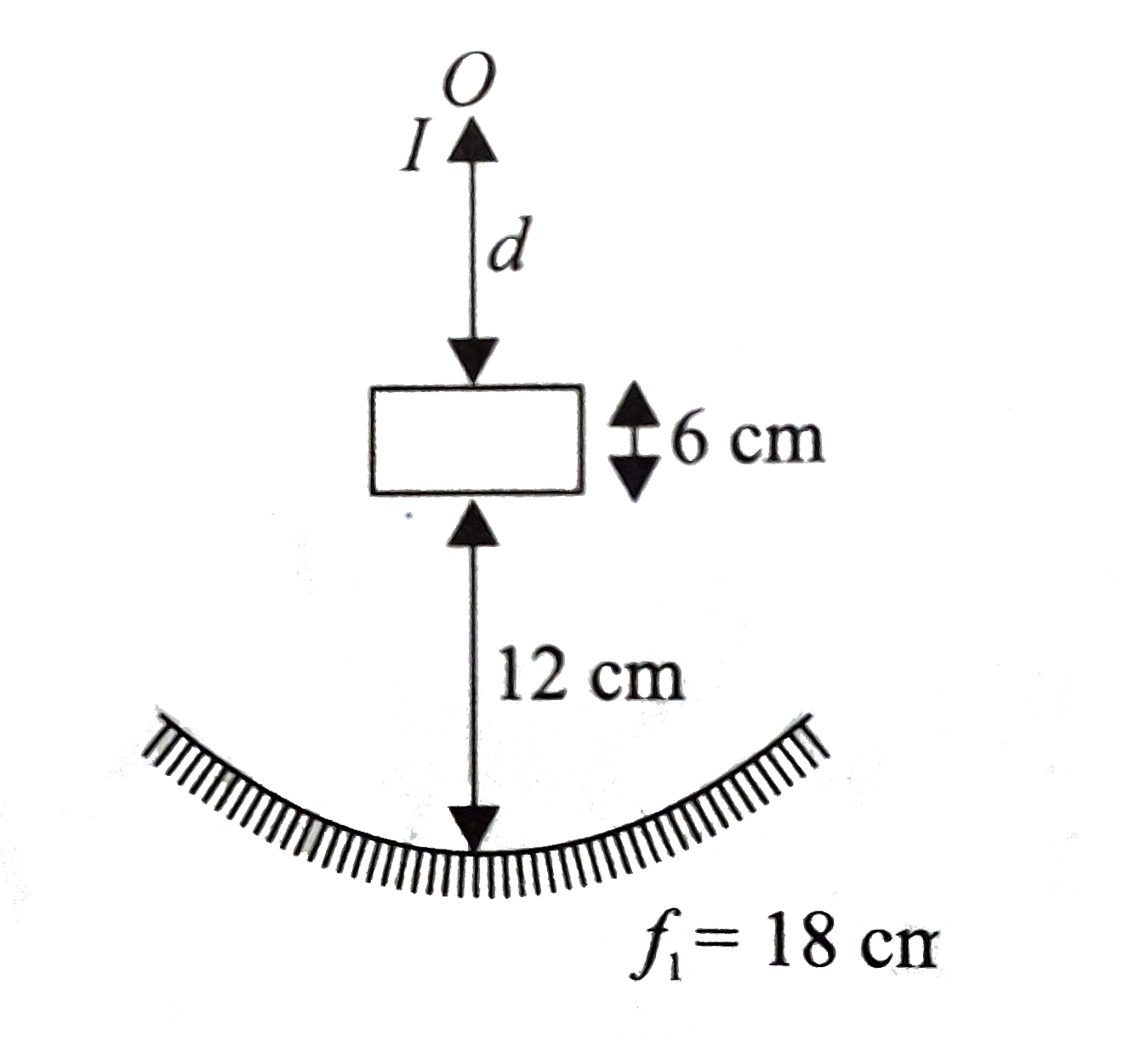
View SolutionA convex lens of focal length 40cm is held at a distance 12cm coaxially above a concave mirror of focale length 18cm.

Q. If the convex lens is replaced by a glass plate of thickness 6cm, refractive index `mu=(3)/(2)` and gives rise to an image coincident with itself, then the value of d is equal to

View SolutionA concave mirror forms real image of a point source lying on the optical axis at a distance of 50cm from the mirror. The focal length of the mirror is 25cm. The mirror is cut in two, and its halves are drawn at a distance of 1 cm apart in a direction perpendicular to the optical axis.

Q. The distance between the two images formed by the two halves of the mirror is
View SolutionA concave mirror forms real image of a point source lying on the optical axis at a distance of 50cm from the mirror. The focal length of the mirror is 25cm. The mirror is cut in two, and its halves are drawn at a distance of 1 cm apart in a direction perpendicular to the optical axis.

Q. Two statements are provided. Choose which is true and which is false.
Statement I: Image formed by half cut mirror has just half the intensity as that of the intensity of image formed by complete mirror.
Statement II: More the lateral separation between the two halves of the mirror, less will be the separation between the two images, as show in the given situation.
View SolutionA concave mirror forms real image of a point source lying on the optical axis at a distance of 50cm from the mirror. The focal length of the mirror is 25cm. The mirror is cut in two, and its halves are drawn at a distance of 1 cm apart in a direction perpendicular to the optical axis.

Q. In the given situation, if the two halves are each rotated (before being separated) about S by `90^(@)`, with reference to original position, then the distance between the two images will be

View SolutionAn object AB of height 1cm lying on the axis of convex mirror of focal length20cm, at a distance of 30cm from its pole as shown in figure. Now the object starts moving with a constant speed `1 cm//sec` towards the pole. Calculate

Q. Magnitude of velocity of image at the given instant
View SolutionAn object AB of height 1cm lying on the axis of convex mirror of focal length20cm, at a distance of 30cm from its pole as shown in figure. Now the object starts moving with a constant speed `1 cm//sec` towards the pole. Calculate
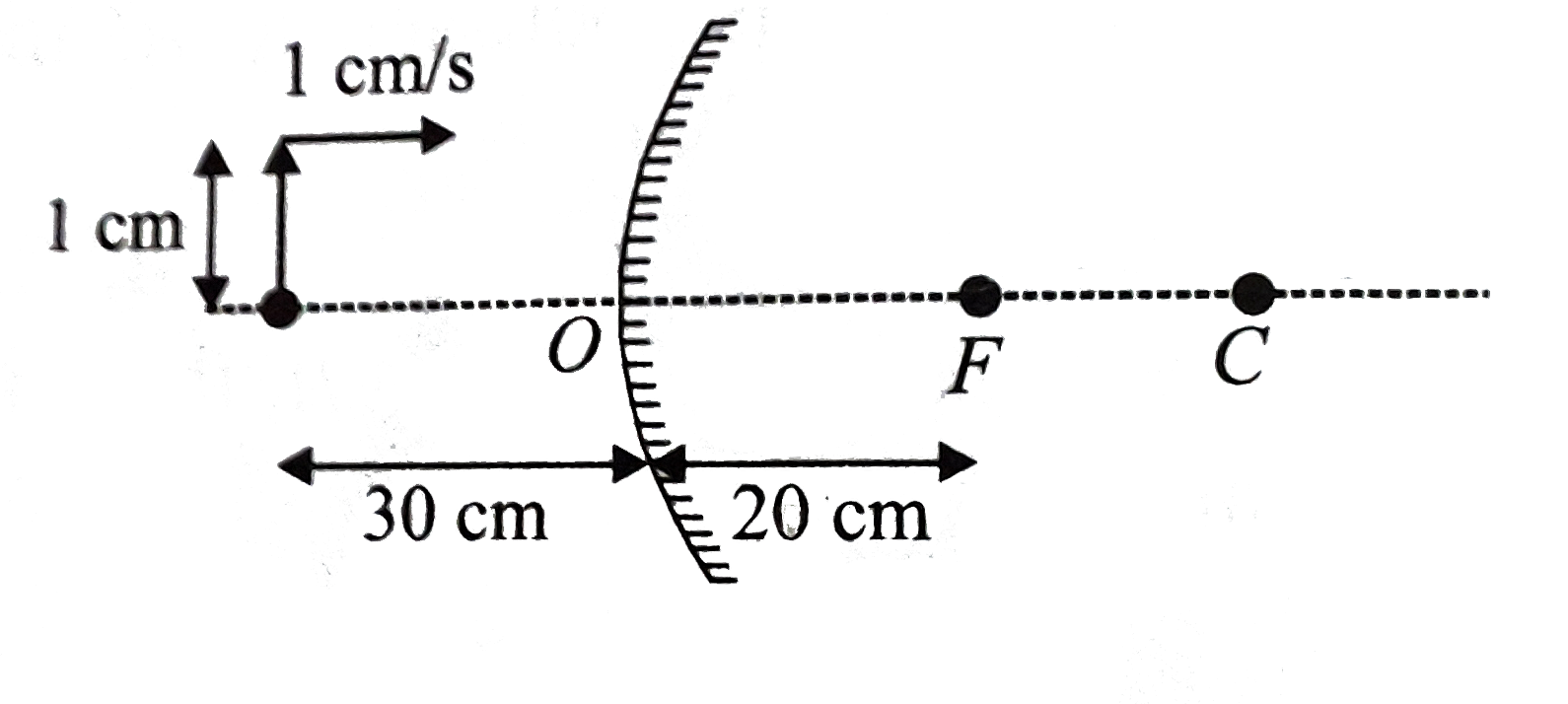
Q. Rate of change of height of image.
View Solution
Linked Comprehension questions and complete solutions for chapter GEOMETRICAL OPTICS of CENGAGE PHYSICS (ENGLISH) of Class 12