Complete Solutions to Elastic Deformation Of Asolid Body of chapter PHYSICAL FUNDAMENTALS OF MECHANICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | PHYSICAL FUNDAMENTALS OF MECHANICS |
| IE IRODOV | Elastic Deformation Of Asolid Body |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
What pressure has to be applied to the ends of a steel cylinder to keep its length constant on raising its temperature by `100.^@C` ?
03:35View SolutionWhat internal pressure (in the absence of an external presure) can be sustained
(a) by a glass tube, (b) by a glass spherical flask, if in both cases the wall thickness is equal to `Deltar=1.0mm` and the radius of the tube and the flask equals `r=25mm`?View SolutionA horizontally orientied unifrom copper rod of length `l` is rotating about a vertical axis passing through its centre. Calculate the rotated frequency at which the rod ruptures. Breaking or rupture strength of copper is `sigma` and density of copper is `rho`.
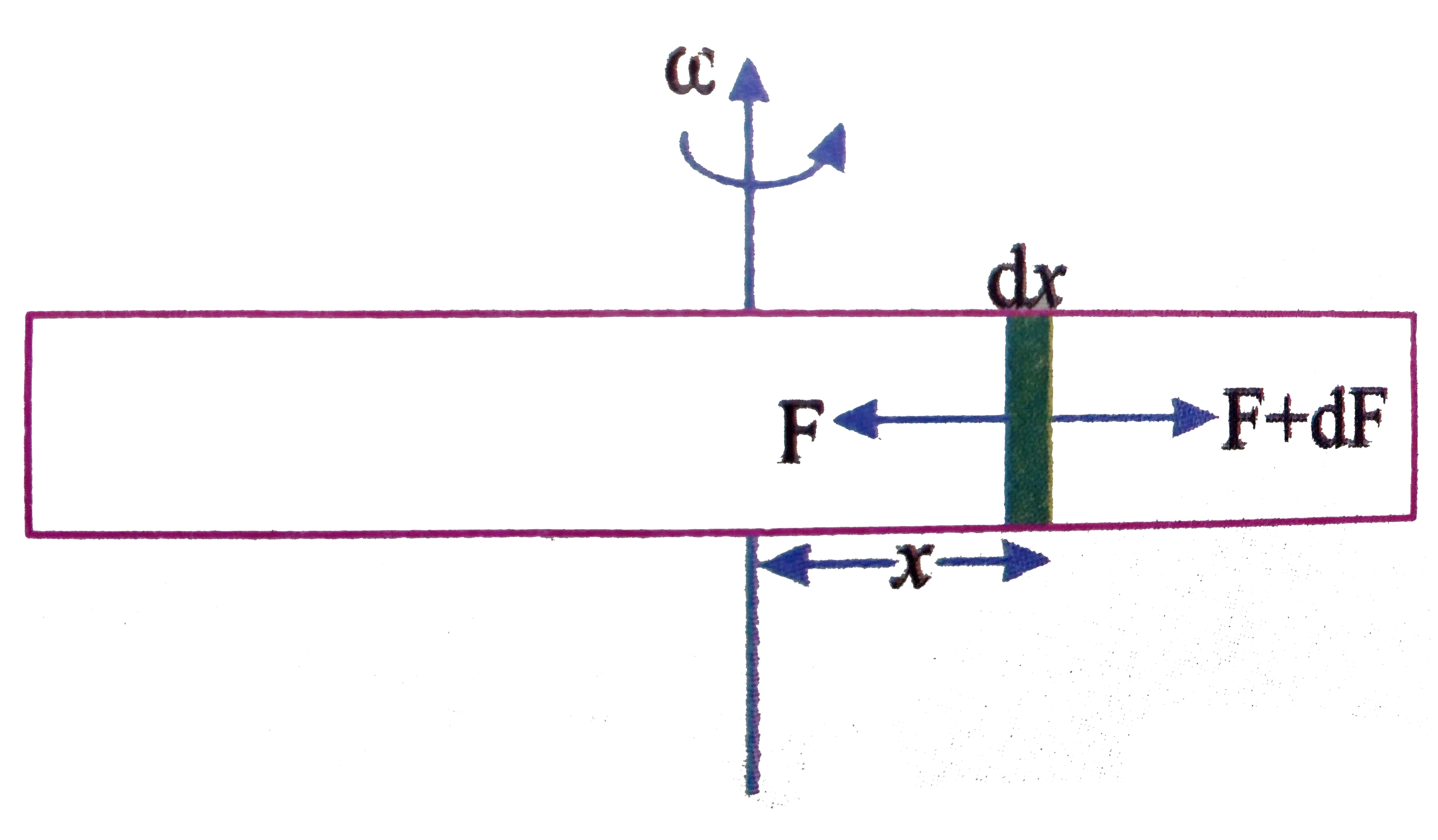 09:21View Solution
09:21View SolutionA ring of radius `r=25cm` made of lead wire is rotated about a stationary vertical axis passing through its centre and perpendicular to the plane of the ring. What is the number of rps at which the ring ruptures?
View SolutionA steel wire of diameter `d=1.0mm` is stretched horizontally between two clamps located at the distance `l=2.0m` from each other. A weight of mass `m=0.25kg` is suspended from the mid-point O of the wire. What will the resulting descent of the point O be in centrimetres?
05:08View SolutionA uniform elastic plank moves due to a constant force `F_(0)` applied at one end whose area is `S`. The Young's modulus of the plank is `Y`. The strain produced in the direction of force is
05:04View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity `omega` in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
05:11View SolutionA solid copper cylinder of length `l=65cm` is placed on a horizontal surface and subjected to a vertical compressive force `F=1000N` directed downward and distributed uniformly over the end face. What will be the resulting change of the volume of the cylinder in cubic millimeters?
03:52View SolutionA copper rod of length l is suspended from the ceiling by one of its ends. Find:
(a) the elongation `Deltal` of the rod due to its own weight ,
(b) the relative increment of its volume `DeltaV//V`.04:40View SolutionA bar made of material whose Young's modulus is equal to E and Poisson's ratio to `mu` is subjected to the hydrostatic pressure p. Find:
(a) the fractional decrement of its volume,
(b) the relationship between the compressibility `beta` and the elastic constants E and `mu`.
Show that Poisson's ratio `mu` cannot exceed `1//2`.View SolutionOne end of a steel rectangular girder is embedded into a wall (figure). Due to gravity it sags slightly. Find the radius of curvature of the neutral layer (see the dotted line in the figure) in the vicinity of the point O if the length of the protruding section of the girder is equal to `l=6.0m` and the thickness of the girder equals `h=10cm`.
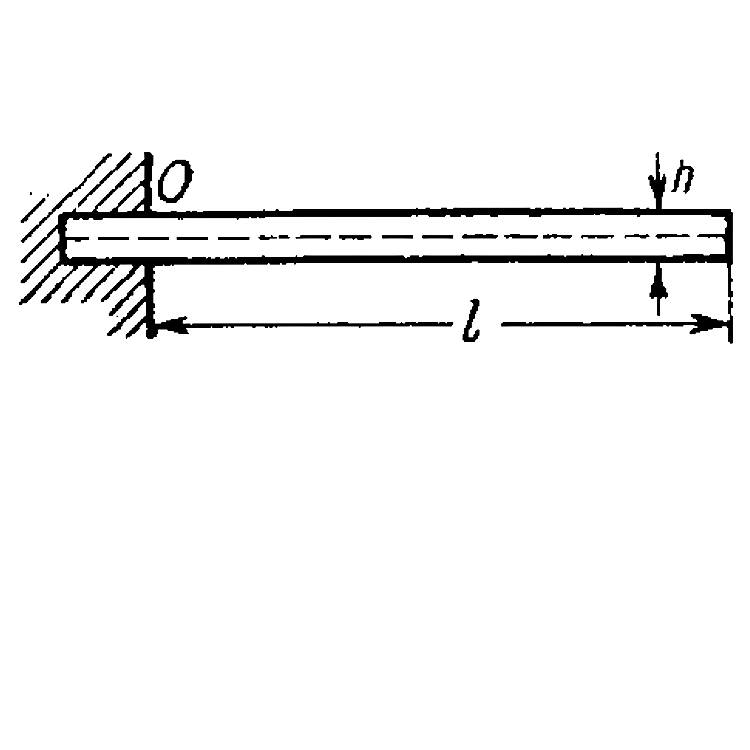 View Solution
View SolutionThe bending of an elastic rod is described by the elastic curve passing through centres of gravity of rod's cross-sections. At small bendings the equation of this curve takes the form
`N(x)=EI(d^2y)/(dx^2)`,
where `N(x)` is the bending moment of the elastic forces in the cross-section corresponding to the x coordinate, E is Young's modulus, I is the moment of inertia of the cross-section relative to the axis pasing through the neutral layer `(I=intz^2dS`, figure)

Suppose one end of a steel rod of a square cross-section with side a is embedded into a wall, the protruding section being of length l (figure). Assuming the mass of the rod to be negligible, find the shape of the elastic curve and the deflection of the rod `lambda`, if its end A experiences
(a) the bending moment of the couple `N_0`, ,
(b) a force F oriented along the y axis.
 View Solution
View SolutionA steel girder of length l rests freely on two supports (figure). The moment of inertia of its cross-section is equal to I (see the foregoing problem). Neglecting the mass of the girder and assuming the sagging to be slight, find the deflection `lambda` due to the force F applied to the middle of the girder.
 View Solution
View SolutionThe thickness of a rectangular steel girder equals h, find the deflection `lambda` caused by the weight of the girder in two cases:
(a) one end of the girder is embedded into a wall with the length of the protruding section being equal to l (figure)

(b) the girder of length `2l` rests freely on two supports (figure).
 View Solution
View SolutionA steel plate of thickness h has the shape of a square whose side equals l, with `h lt lt l`. The plate is rigidly fixed to a vertical axle OO which is rotated with a constant angular acceleration `beta` (figure). Find the deflection `lambda`, assuming the sagging to be small.
 View Solution
View SolutionDetermine the relationship between the torque N and the torsion angle `varphi` for
(a) the tube whose wall thickness `Deltar` is considerably less than the tube radius,
(b) for the solid rod of circular cross-section. Their lengh l, radius r, and shear modulus G are supposed to be known.View SolutionCalculate the torque N twisting a steel tube of length `l=3.0m` through an angle `varphi=2.0^@` about its axis, if the inside and outside diameters of the tube are equal to `d_1=30mm` and `d_2=50mm`.
03:41View SolutionFind the maximum power which can be transmitted by means of a steel shaft rotating about its axis with an angular velocity `omega=120rad//s`, if its length `l=200cm`, radius `r=1.50cm`, and the permissible torsion angle `varphi=2.5^@`.
03:13View SolutionA uniform ring of mass `m`, with the outside radius `r_2`, is fitted tightly on a shaft of radius `r_1`. The shaft is rotated about its axis with a constant angular acceleration `beta`. Find the moment of elastic forces in the ring as a function of the distance r from the rotation axis.
View SolutionFind the elastic deformation energy of a steel rod of mass `m=3.1kg` stretched to a tensile strain `epsilon=1.0*10^-3`.
02:58View SolutionA steel cylindrical rod of length `l` and radius `r` is suspended by its end from the ceiling.
(a) Find the elastic deformation energy U of the rod.
(b) Define U in terms of tensile strain `Deltal//l` of the rod.07:01View SolutionWhat work has to be performed to make a hoop out of a steel band of length `l=2.0m`, width `h=6.0cm`, and thickness `delta=2.0mm`? The process is assumed to proceed within the elasticity range of the material.
View SolutionFind the elastic deformation energy of a steel rod whose one end is fixed and the other is twisted through an angle `varphi=6.0^@`. The length of the rod is equal to `l=1.0m`, and the radius to `r=10mm`.
03:08View SolutionFind how the volume density of the elastic deformation energy is distributed in a steel rod depending on the distance r from its axis. The length of the rod is equal to l, the torsion angle to `varphi`.
View SolutionFind the volume density of the elastic deformation energy in fresh water at the depth of `h=1000m`.
02:50View Solution
Elastic Deformation Of Asolid Body questions and complete solutions for chapter PHYSICAL FUNDAMENTALS OF MECHANICS of IE IRODOV PHYSICS (HINGLISH) of Class 12
