Complete Solutions to Dynamics Of A Solid Body of chapter PHYSICAL FUNDAMENTALS OF MECHANICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | PHYSICAL FUNDAMENTALS OF MECHANICS |
| IE IRODOV | Dynamics Of A Solid Body |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
A thin uniform rod AB of mass `m=1.0kg` moves translationally with acceleration `w=2.0m//s^2` due to two antiparallel forces `F_1` and `F_2` (figure). The distance between the points at which these forces are applied is equal to `a=20cm`. Besides, it is known that `F_2=5.0N`. Find the length of the rod.
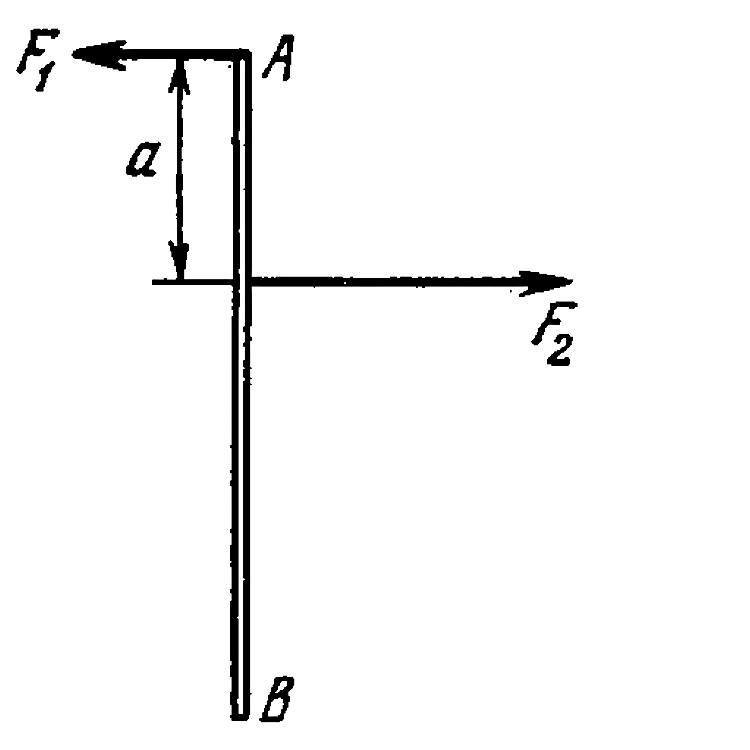 04:46View Solution
04:46View SolutionA force `F=Ai+Bj` is applied to a point whose radius vector relative to the origin of coordinates O is equal to `r=ai+bj`, where a, b, A, B are constants, and i,j are the unit vectors of the x and y axes. Find the moment N and the arm l of the force F relative to the point O.
05:04View SolutionA force `F_1=Aj` is applied to a point whose radius vector `r_1=ai`, while a force `F_2=Bi` is applied to the point whose radius vector `r_2=bj`. Both radius vectors are determined relative to the origin of coordinates O, i and j are the unit vectors of the x and y axes, a, b, A, B are constants. Find the arm l of the resultant force relative to the point O.
06:12View SolutionThree forces are applied to a square plate as shown in Figure. Find the modulus, direction, and the point of application of the resultant force, if this point is taken on the side BC.
 09:37View Solution
09:37View SolutionFind the moment of inertia
(a) of a thin uniform rod relative to the axis which is perpendicular to the rod and passes through its end, if the mass of the rod is m and its lengh l,
(b) of a thin uniform rectangular plate relative to the axis passing perpendicular to the plane of the plate through one of its vertices, if the sides of the plate are equal to a and b, and its mass is m.12:31View SolutionCalculate the moment of inertia
(a) of a copper uniform disc relative to the symmetry axis perpendicular to the plane of the disc, if its thickness is equal to `b=2.0mm` and its radius to `R=100mm`,
(b) of a uniform solid cone relative to its symmetry axis, if the mass of the cone is equal to m and the radius of its base to R.12:49View SolutionDemonstrate that in the case of a thin plate of arbitrary shape there is the following relationship 1, 2, and 3 define three mutually perpendicular axes passing through one point, with axes 1 and 2 lying in the plane of the plate. Using this relationship, find the moment of inertia of a thin uniform round disc of radius R and mass m relative to the axis coinciding with one of its diameters.
View SolutionA uniform disc of radius `R=20cm` has a round cut as shown in figure. The mass of the remaining (shaded) portion of the disc equals `m=7.3kg`. Find the moment of inertia of such a disc relative to the axis passing through its centre of inertia and perpendicular to the plane of the disc.
 12:18View Solution
12:18View SolutionUsing the formula for the moment of inertia of a uniform sphere, find the moment of inertia of a thin spherical layer of mass m and radius R relative to the axis passing through its centre.
12:10View SolutionA light thread with a body of mass `m` tied to its end is wound on a uniform solid cylinder of mass `M` and radius `R`. At a moment `t=0` the system is set in motion. Assuming the friction in the axle of the cylinder to be negligible, find the time dependence of
(a) the angular velocity of the cylinder and
(b) the kinetic energy of the whole system ( `M=2m`).
 06:43View Solution
06:43View SolutionThe ends of thin threads tightly wound on the axle of radius r of the Maxwell disc are attached to a horizontal bar. When the disc unwinds, the bar is raised to keep the disc at the same height. The mass of the disc with the axle is equal to m, the moment of inertia of the arrangement relative to its axis is I. Find the tension of each thread and the acceleration of the bar.
05:36View SolutionA thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment the end B starts experiencing a constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizonatal plane. Find the angular velocity of the rod as a function of its rotation angle `varphi` counted relative to the initial position.
06:00View Solution
In the arrangement shown in figure the mass of the uniform solid cylindrical pulley of radius `R` is equal to `m` and the masses of two bodies are equal to `m_(1)` and `m_(2)`. The thread slipping and the friction in the axle of the pulley are supposed to be absent. Find the angular acceleration of the cylinder and the ratio of tensions `(T_(1))/(T_(2))` of the vertical sections of the thread in the process of motion.07:47View SolutionIn the system shown in figure the masses of the bodies are known to be `m_1` and `m_2`, the coefficient of friction between the body `m_1` and the horizontal plane is equal to `k`, and a pulley of mass m is assumed to be a uniform disc. The thread does not slip over the pulley. At the moment `t=0` the body `m_2` starts descending. Assuming the mass of the thread and the friction in the axle of the pulley to be negligible, find the work performed by the friction forces acting on the body `m_1` over the first t seconds after the beginning of motion.
 13:52View Solution
13:52View SolutionA uniform cylinder of radius `R` is spinned about it axis to the angular velocity `omega_(0)` and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is `mu_(k)` How many turns will the cylinder accomplish before it stops?
 06:56View Solution
06:56View SolutionA uniform disc of radius R is spinned to the angular velocity `omega` and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be neglected as uniform.
08:47View SolutionA flywheel with the initial angular velocity `omega_0` decelerates due to the forces whose moment relative to the axis is proportional to the square root of its angular velocity. Find the mean angular velocity of the flywheel averaged over the total decleration time.
07:47View SolutionA uniform cylinder of radius `r` and mass `m` can rotate freely about a fixed horizontal axis. A thin cord of length l and mass `m_(0)` is would on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length `x` of the hanging part of the end. the wound part of the cord is supposed to have its centre of gravity on the cylinder axis is shown in figure.
 04:49View Solution
04:49View SolutionA uniform sphere of mass `m` and radius `R` rolls without slipping down an inclined plane set at an angle `theta` to the horizontal. Find
(`a`) the friction coefficient at which slipping is absent,
(`b`) the kinetic energy of the sphere `t` seconds after the beginning of motion.17:08View SolutionA uniform cylinder of mass `m` and radius `R` starts descending at a moment `t=0` due to gravity, Neglecting the mass of the thread, find
(a) the tension of each thread and the angular acceleration of the cylinder,
(b) the time dependence of the instantaneous power developed by the gravitational force.
 09:02View Solution
09:02View SolutionThin threads are tightly wound on the ends of a uniform solid cylinder of mass m. The free ends of the threads are attached to the ceiling of an elevator car. The car starts going up with an acceleration `w_0`. Find the acceleration `w^'` . Find the acceleration `w^'` of the cylinder relative to the car and the force F exerted by the cylinder on the ceiling (through the threads).
View SolutionA spool with a thread wound on it is placed on an inclined smooth plane set an angle `alpha=30^@` to the horizontal. The free end of the thread is attached to the wall as shown in figure. The mass of the spool is `m=200g`, its moment of inertia relative to its own axis `I=0.45g*m^2`, the radius of the wound thread layer `r=3.0cm`. Find the acceleration of the spool axis.
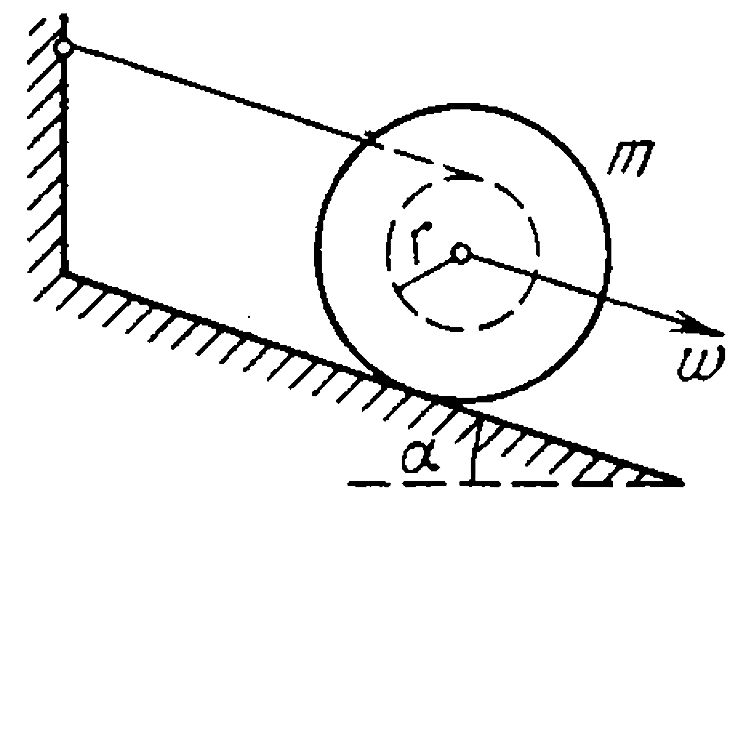 04:30View Solution
04:30View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F(figure).
Find the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to k. What is the acceleration `w_(max)` of the axis of the cylinder rolling down the inclined plane?
 09:24View Solution
09:24View SolutionA spool with thread wound on it, of mass m, rests on a rough horizontal surface. Its moment of inertia relative to its own axis is equal to `I=gammamR^2`, where `gamma` is a numerical factor, and R is the outside radius of the spool. The radius of the wound thread layer is equal to r. The spool is pulled without sliding by the thread with a constant force F directed at an angle `alpha` to the horizontal (figure). Find:
(a) the projection of the acceleration vector of the spool axis on the x-axis,
(b) the work performed by the force F during the first t seconds after the beginning of motion.
 07:16View Solution
07:16View SolutionThe arrangement shown in figure consists of two identical, uniform, solid cylinders, each of mass `m`, on which two light theads are wound symmetrically.
Find the tensions of each thread in the process of motion. The friction in the axle of the upper cylinder is assumed to be absent.
 03:46View Solution
03:46View SolutionIn the arrangement shown in figure a weight A possesses mass m, a pulley B possesses mass M. Also known are the moment of inertia I of the pulley relative to its axis and the radii of the pulley R and `2R`. The mass of the threads is negligible. Find the acceleration of the weight A after the system is set free.
 06:38View Solution
06:38View SolutionA uniform solid cylinder A of mass `m_1` can freely rotate about a horizontal axis fixed to a mount B of mass `m_2`(figure). A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find:
(a) the acceleration of the point K,
(b) the kinetic energy of this system t seconds after the beginning of motion.
 08:28View Solution
08:28View SolutionA plank of mass `m_1` with a uniform sphere of mass `m_2` placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what acceleration will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere?
08:32View SolutionA uniform solid cylinder of mass `m` and radius `R` is set in rotation about its axis with an angular velocity `omega_(0)`, then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to `mu`. Find
(`a`) how long the cylinder will move with sliding,
(`b`) the total work performed by the sliding friction force acting on the cylinder.12:17View SolutionA uniform ball of radius `r` rolls without slipping down from the top of a sphere of radius `R` Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
10:02View SolutionA uniform solid cylinder of radius `R=15cm` rolls over a horizontal plane passing into an inclined plane forming an angle `alpha=30^@` with the horizontal(figure). Find the maximum value of the velocity `v_0` which still permits the cylinder to roll onto the inclined plane section without a jump. The sliding is assumed to be absent.
 13:21View Solution
13:21View SolutionA small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane, at the moments when the body A gets into the lower position, the centre of the hoop moves with velocity `v_0`(figure). At what values of `v_0` will the hoop move without bouncing?
 12:18View Solution
12:18View SolutionCalculate the kinetic energy of a tractor crawler belt of mass `m` if the tractor moves with a velocity `v`. There is no slipping. Neglect the size of the wheels.
 01:39View Solution
01:39View SolutionA uniform sphere of mass `m` and radius `r` rolls without sliding over a horizontal plane, rotating ahout a horizontal axle `OA`. In the process, the centre of the sphere moves with a veocity `v` along a circle of radius `R`. Find the kinetic energy of the sphere.
05:54View SolutionDemonstrate that in the reference frame rotating with a constant angular velocity `omega` about a stationary axis a body of mass m experiences the resultant
(a) centrifugal force of inertia `F_(cf)=momega^2R_C`, where `R_C` is the radius vector of the body's centre of inertia relative to the rotation axis,
(b) Coriolis force `F_(cor)=2m[v_C^'omega]`, where `v_C^'` is the velocity of the body's centre of inertia in the rotating reference frame.View SolutionA midpoint of a thin uniform rod AB of mass `m` and length `l` is rigidly fixed to a rotation axle `OO^'` as shown in figure. The rod is set into rotation with a constant angular velocity `omega`. Find the resultant moment of the centrifugal forces of inertia relative to the point C in the reference frame fixed to the axle `OO^'` and to the end.
 05:41View Solution
05:41View SolutionA conical pendulum, a thin uniform rod of length `l` and mass `m`, rotates uniformly about a vertical axis with angular velocity `omega`(the upper end of the rod is hinged). Find the angle `theta` between the rod and the vertical.
06:27View SolutionA uniform cube with edge a rests on a horizontal plane whose friction coefficient equals k. The cube is set in motion with an intial velocity, travels some distance over the plane and comes to a stand still. Explain the disappearance of the angular momentum of the cube relative to the axis lying in the plane at right angles to the cube's motion direction. Find the distance between the resultants of gravitational forces and the reaction forces exerted by the supporting plane.
06:22View SolutionA smooth uniform rod AB of mass M and length l rotates freely with an angular velocity `omega_0` in a horizontal plane about a stationary vertical axis passing through its end A. A small sleeve of mass m starts sliding along the rod from the point A. Find the velocity `v^'` of the sleeve relative to the rod at the moment it reaches its other and B.
11:15View SolutionA uniform rod of mass `m=5.0kg` and length `l=90cm` rests on a smooth horizontal surface. One of the ends of the rod is struck with the impulse `J=3.0N*s` in a horizontal direction perpendicular to the rod. As a result, the rod obtains the momentum `p=3.0N*s`. Find the force with which one half of the rod will act on the other in the process of motion.
09:20View SolutionA thin uniform square plate with side l and mass M can rotate freely about a stationary vertical axis coinciding with one of its sides. A small ball of mass m flying with velocity v at right angles to the plate strikes elastically the centre of it. Find:
(a) the velocity of the ball `v^'` after the impact,
(b) the horizontal component of the resultant force which the axis will exert on the plate after the impact.10:23View SolutionA vertically oriented uniform rod of mass M and length l can rotate about its upper end. A horizontally flying bullet of mass m strikes the lower end of the rod and gets stuck in it, as a result, the rod swings through an angle `alpha`. Assuming that `m lt lt M`, find:
(a) the velocity of the flying bullet,
(b) the momentum increment in the system "bullet-rod" during the impact, what causes the change of that momentum,
(c) at what distance x from the upper end of the rod the bullet must strike for the momentum of the system "bullet-rod" to remain constant during the impact.20:24View SolutionA horizontally oriented uniform disc of mass `M` and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass `m`. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with and angular velocity `omega_(0)`. Then by means of a force `F` applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.08:49View SolutionA man of mass `m_1` stands on the edge of a horizontal uniform disc of mass `m_2` and radius R which is capable of rotating freely about a stationary vertical axis passing through its centre. At a certain moment the man starts moving along the edge of the disc, he shifts over an angle `varphi^'` relative to the disc and then stops. In the process of motion the velocity of the man varies with time as `v^'(t)`.
Assuming the dimensions of the man to be negligible, find:
(a) the angle through which the disc had turned by the moment the man stopped,
(b) the force moment (relative to the rotation axis) with which the man acted on the disc in the process of motion.08:34View SolutionTwo horizontal discs rotate freely about a vertical axis passing through their centres. The moments of inertia of the discs relative to this axis are equal to `I_1` and `I_2`, and the angular velocities to `omega_1` and `omega_2`. When the upper disc fell on the lower one, both discs began rotating, after some time, as a single whole (due to friction). Find:
(a) teh steady-state angular rotation velocity of the discs,
(b) the work performed by the friction forces in this process.07:24View SolutionA small disc and a thin uniform rod of length l, whose mass is `eta` times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horiozontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of `eta` will the velocity of the disc after the collision be equal to zero? reverse its direction?
15:17View SolutionA stationary platform P which can rotate freely about a vertical axis (figure) supports a motor M and a balance weight N. The moment of inertia of the platform with the motor and the balance weight relative to this axis is equal to I. A light frame is fixed to the motor's shaft with a uniform sphere A rotating freely with an angular velocity `omega_0` about a shaft `BB^'` coinciding with the axis `OO^'`. The moment of inertia of the sphere relative to the rotation axis is equal to `I_0`. Find
(a) the work performed by the motor in turning the shaft `BB^'` through `90^@`, through `180^@`,
(b) the moment of external forces which maintains the axis of the arrangement in the vertical position after the motor turns the shaft `BB^'` through `90^@`.
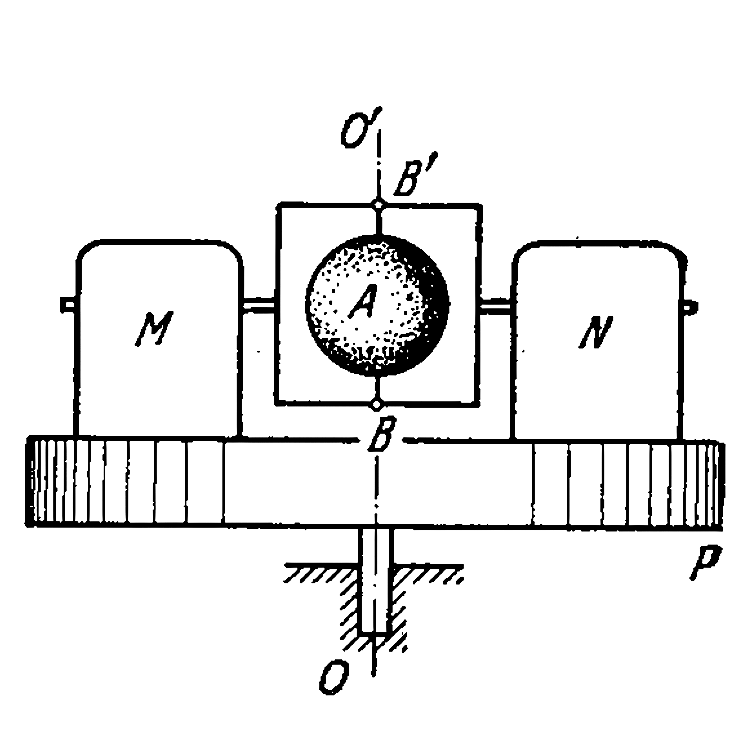 16:52View Solution
16:52View SolutionA horizontally oriented uniform rod AB of mass `m=1.40kg` and length `l_0=100cm` rotates freely about a stationary vertical axis `OO^'` passing through its end A. The point A is located at the middle of the axis `OO^'` whose length is equal to `l=55cm`. At what angular velocity of the rod the horizontal component of the force acting on the lower end of the axis `OO^'` is equal to zero? What is in this case the horizontal component of the force acting on the upper end of the axis?
09:09View SolutionThe middle of a uniform rod of mass m and length l is rigidly fixed to a vertical axis `OO^'` so that the angle between the rod and the axis is equal to `theta` (figure). The ends of the axis `OO^'` are provided with bearings. The system rotates without friction with an angular velocity `omega`. Find:
(a) the magnitude and direction of the rod's angular momentum M relative to the point C, as well as its angular momentum relative to the rotation axis,
(b) how much the modulus of the vector M relative to the point C increases during a half-turn,
(c) the moment of external forces N acting on the axle `OO^'` in the process of rotation.
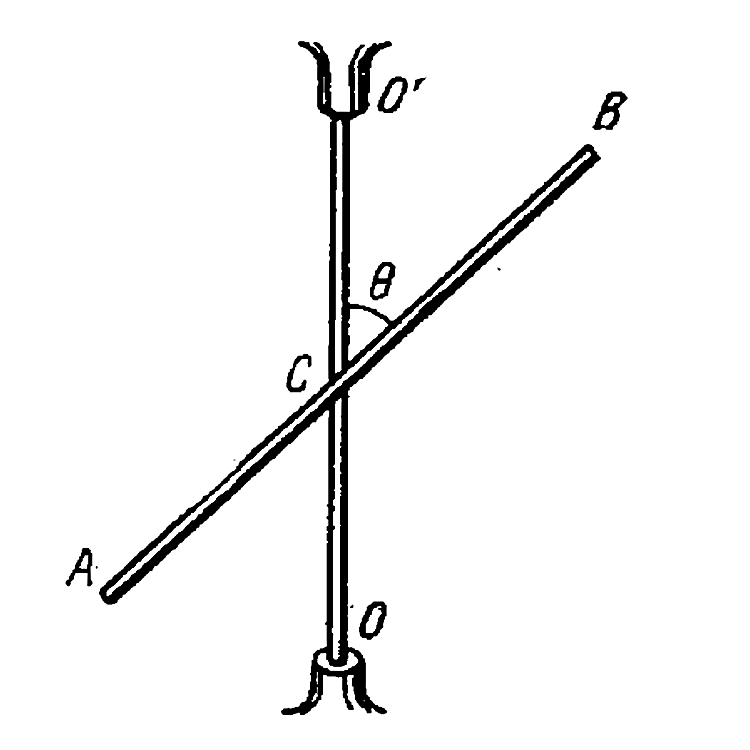 View Solution
View SolutionA top of mass `m=0.50kg`, whose axis is tilted by an angle `theta=30^@` to the vertical, precesses due to gravity. The moment of inertia of the top relative to its symmetry axis is equal to `I=2.0g*m^2`, the angular velocity of rotation about that axis is equal to `omega=350rad//s`, the distance from the point of rest to the centre of inertia of the top is `l=10cm`. Find:
(a) the angular velocity of the top's precession,
(b) the magnitude and direction of the horizontal component of the reaction force acting on the top at the point of rest.12:53View SolutionA gyroscope, a uniform disc of radius `R=5.0cm` at the end of a rod of length `l=10cm` (figure), is mounted on the floor of an elevator car going up with a constant acceleration `w=2.0m//s^2`. The other end of the rod is hinged at the point O. The gyroscope precesses with an angular velocity `n=0.5 rps`. Neglecting the friction and the mass of the rod, find the proper angular velocity of the disc.
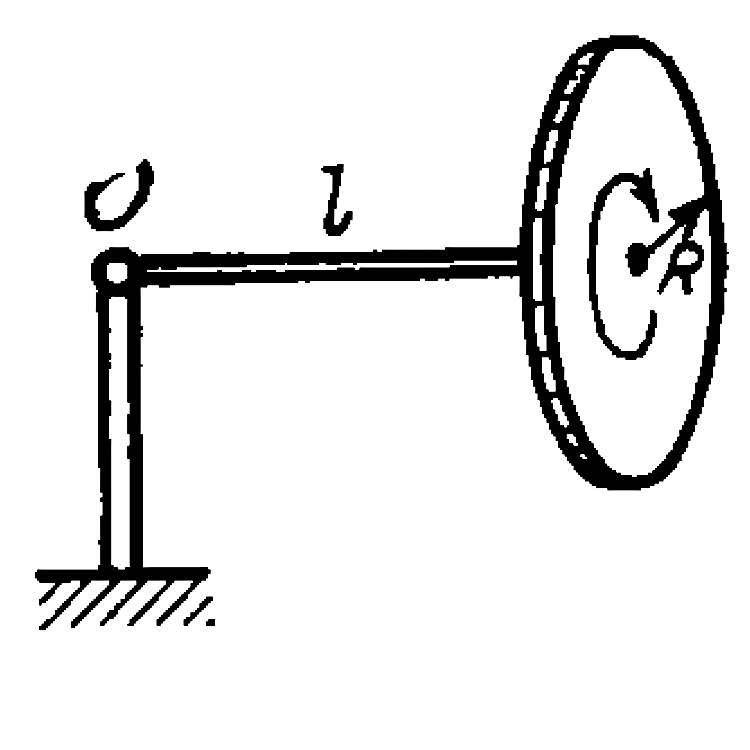 View Solution
View SolutionA top of mass `m=1.0kg` and moment of inertia relative to its own axis `I=4.0g*m^2` spins with an angular velocity `omega=310rad//s`. Its point of rest is located on a block which is shifted in a horizontal direction with a constant acceleration `w=1.0m//s^2`. The distance between the point of rest and the centre of inertia of the top equals `l=10cm`. Find the magnitude and direction of the angular velocity of precession `omega^'`.
View SolutionA uniform sphere of mass `m=5.0kg` and radius `R=6.0cm` rotates with an angular velocity `omega=1250rad//s` about a horizontal axle passing through its centre and fixed on the mounting base by means of bearings. The distance between the bearings equals `l=15cm`. The base is set in rotation about a vertical axis with an angular velocity `omega^'=5.0rad//s`. Find the modulus and direction of the gyroscopic forces.
06:45View SolutionA cylindrical disc of a gyroscope of mass `m=15kg` and radius `r=5.0cm` spins with an angular velocity `omega=330rad//s`. The distance between the bearings in which the axle of the disc is mounted is equal to `l=15cm`. The axle is forced to oscillate about a horizontal axis with a period `T=1.0s` and amplitude `varphi_m=20^@`. Find the maximum value of the gyropscopic forces exerted by the axle on the bearings.
View SolutionA ship moves with velocity `v=36km` per hour along an arc of a circle of radius `R=200m`. Find the moment of the gyroscopic forces exerted on the bearings by the shaft with a flywheel whose moment of inertia relative to the rotation axis equals `I=3.8*10^3 kg*m^2` and whose rotation velocity `n=300rpm`. The rotation axis is oriented along the length of the ship.
03:33View SolutionA locomotive is propelled by a turbine whose axle is parallel to the axes of wheels. The turbine's rotation direction coincides with that of wheels. The moment of inertia of the turbine rotor relative to its own axis is equal to `I=240kg*m^2`. Find the additional force exerted by the gyroscopic forces on the rails when the locomotive moves along a circle of radius `R=250m` with velocity `v=50km` per hour. The gauge is equal to `l=1.5m`. The angular velocity of the turbine equals `n=1500rpm`.
03:30View Solution
Dynamics Of A Solid Body questions and complete solutions for chapter PHYSICAL FUNDAMENTALS OF MECHANICS of IE IRODOV PHYSICS (HINGLISH) of Class 12
