Complete Solutions to Section-III (Paragraph) of chapter JEE ADVANCED of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | JEE ADVANCED |
| JEE ADVANCED | Section-III (Paragraph) |
| Number Of Questions | 5 |
| Academic Year | 2023-24 |
When a particle of mass m moves on the x-axis in a potential of the form `V(x) =kx^(2)` it performs simple harmonic motion. The correspondubing time period is proprtional to `sqrtm/h`, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of `x=0` in a way different from `kx^(2)` and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is `V(x)=ax^(4)(agt0)` for |x| neat the origin and becomes a constant equal to `V_(0)` for |x|impliesX_(0)` (see figure).
(##JMA_CHMO_C10_031_Q01##)
If total energy of the particle is E, it will perform perildic motion only if.04:24View SolutionWhen a particle of mass m moves on the x-axis in a potential of the form `V(x) =kx^(2)` it performs simple harmonic motion. The correspondubing time period is proprtional to `sqrtm/h`, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of `x=0` in a way different from `kx^(2)` and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is `V(x)=ax^(4)(agt0)` for |x| neat the origin and becomes a constant equal to `V_(0)` for |x|impliesX_(0)` (see figure).
(##JMA_CHMO_C10_032_Q01##).
For periodic motion of small amplitude A,the time period (T) of thes particle is proportional to.02:33View SolutionWhen a particle of mass m moves on the x-axis in a potential of the form `V(x) =kx^(2)` it performs simple harmonic motion. The correspondubing time period is proprtional to `sqrtm/h`, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of `x=0` in a way different from `kx^(2)` and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is `V(x)=ax^(4)(agt0)` for |x| neat the origin and becomes a constant equal to `V_(0)` for |x|impliesX_(0)` (see figure).
(##JMA_CHMO_C10_033_Q01##).
The acceleration of this partile for `|x|gtX_(0)` is
(a) proprtional to `V_(0)`
(b) proportional to.01:49View SolutionElectrical resistance of certain materials, known as superconductors, changes abruptly from a nonzero value of zero as their temperature is lowered below a critical temperature `T_(C) (0)`. An interesting property of super conductors is that their critical temperature becomes smaller than `T_(C) (0)` if they are placed in a magnetic field, i.e., the critical temperature `T_(C) (B)` is a function of the magnetic field strength B. The dependence of `T_(C) (B)` on B is shown in the figure.
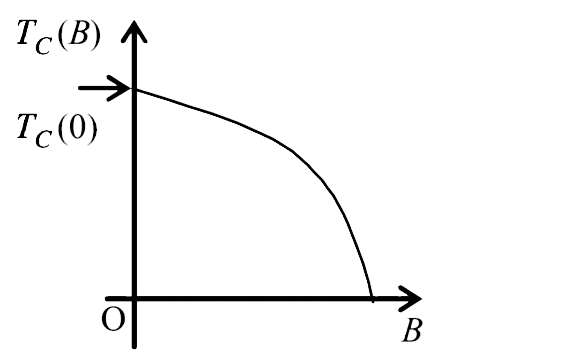 .
.
In the graphs below, the resistance R of a superconductor is shown as a function of its temperature T for two different magnetic fields `B_1`(solid line) and `B_2` (dashed line). If `B_2` is larget than `B_1` which of the following graphs shows the correct variation of R with T in these fields?07:41View SolutionElectrical resistance of certain materials, known as superconductors, changes abruptly from a nonzero value of zero as their temperature is lowered below a critical temperature `T_(C) (0)`. An interesting property of super conductors is that their critical temperature becomes smaller than `T_(C) (0)` if they are placed in a magnetic field, i.e., the critical temperature `T_(C) (B)` is a function of the magnetic field strength B. The dependence of `T_(C) (B)` on B is shown in the figure.
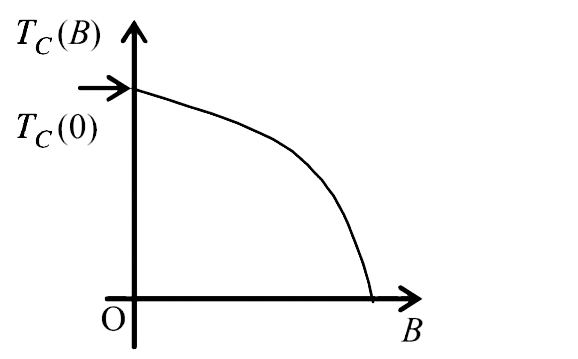 .
.
A superconductor has `T_(C) (0) = 100 K`. When a magnetic field of 7.5 Tesla is applied , its `T_(C)` decreases to 75 K. For this material one can difinitely say that when05:29View Solution
Section-III (Paragraph) questions and complete solutions for chapter JEE ADVANCED of JEE ADVANCED PREVIOUS YEAR of Class 12
All Exercises from JEE ADVANCED Class 12 PHYSICS JEE ADVANCED
- MULTIPLE CHOICE QUESTIONS
- PART I : PHYSICS (SECTION -1)
- PART I : PHYSICS (SECTION -2)
- PART I : PHYSICS (SECTION -3)
- PART I : PHYSICS (SECTION 1)
- PART I : PHYSICS (SECTION 3)
- Part I : PHYSICS (Section 3)Paragraph 2
- PART I: PHYSICS SECTION-2: (Paragraph Type)
- PART I: PHYSICS SECTION-3: (Paragraph Type)
- PART I: PHYSICS Section-3:(Matching List Type)
- PART I: PHYSICS (SECTION-1) (One or more options correct Type)
- PART-1 PHYSICS (SECTION 1 )
- PART-1 PHYSICS (SECTION 2 )
- PART-1 PHYSICS (SECTION 3 )
- PHYSICS
- PHYSICS SECTION - I : Single correct Answer Type
- PHYSICS SECTION - II : Multiple correct Answer Type
- PHYSICS SECTION - III Integer Answer Type
- PHYSICS SECTION - IV Matrix Match Type
- SECTION - 1 (ONE OR MORE THAN ONE OPTIONS CORRECT TYPE)
- SECTION - 1 (ONLY ONE OPTION CORRRECT TYPE)
- Section - I Single correct Answer Type
- Section - II (Multiple correct Answer Type)
- Section - III (Paragraph Type)
- Section - IV (Integer Answer Type)
- Section -(III) (Paragraph type)
- SECTION -1
- SECTION -2
- SECTION -2 ( ONE INTEGER VALUES CORRECT TYPE)
- SECTION -2 COMPREHENSION TYPE
- SECTION -3 (MATCHING LIST TYPE)
- Section -IV (Integer type)
- Section -IV (matrix type)
- SECTION 1
- SECTION 2
- SECTION 3 PARAGRAPH 3
- Section I : Single Correct Answer Type
- Section II : Paragraph Type
- Section III : Multiple Correct Answer(s) Type
- Section-1
- Section-2
- SECTION-I (Single correct Choice Type )
- Section-I (single correct choice type)
- SECTION-I( Single Correct Choice Type )
- Section-II (Integer type)
- SECTION-II ( Multiple Correct Choice Type )
- SECTION-II (Multiple correct Choice Type )
- Section-II (Multiple correct choice type)
- SECTION-III ( Comprehension Type )
- SECTION-III (Comprehension Type )
- Section-III (Paragraph)
- SECTION-IV (Integer Answer Type )
- SECTION-IV( Matrix-Match Type )
