Complete Solutions to Illustration of chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATIC POTENTIAL AND CAPACITANCE |
| NARAYANA | Illustration |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
Determine the potential at a point 0.50 m (i) from a`+20 muC` potential charge (ii) from a`-20 muC` point charge.
View SolutionA charge `+q` is fixed at each of the points `x=x_0`, `x=3x_0`, `x=5x_0`,…………`x=oo` on the x axis, and a charge `-q` is fixed at each of the points `x=2x_0`, `x=4x_0`, `x=6x_0`, …………`x=oo`. Here `x_0` is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be `Q//(4piepsilon_0r)`.Then, the potential at the origin due to the above system of
View SolutionInfinite charges of magnitude `q` each are lying at `x= 1,2,4,8….meter` on `X`-axis. The value of intensity of electric field at point `x=0` due to these charges will be
View SolutionIn the given figure, there are four point charges placed at the vertices of a square of side a= 1.4m. If `q_(1) = +18nC, q_(2) = 24nC, q_(30 = +35nC and q_(4) = +16nC`, then find the electrid potential at the centre P of the square. Assume the potential to be zero at infintiy.

View SolutionIf 100 J of work must be done to move electric charge equal tp 4C from a place where potential is `-10V` to another place where potential si V volt, find the value of V.
View SolutionA charge of 10C is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J. What is the potential difference
`(V_(A) - V_(B))` ?
View SolutionSuppose an electron in the picture tube of a television set is accelerated from rst through a potential differencre `V_(b) - V_(a) = V_(ba) =+` 5000V
(a) What is the change in electric potential energy of the electron?
(b) What is the speed of the electron `(m = 9.1 xx 10^(31)kg)` as a result of this acceleration?
View SolutionA particle of mass m and positive charge q is released from point A. Its speed is found to be v when it passes through a point B. which of the two points is at higher potential ? What is the potential difference between the points?
View SolutionCharge `q_(1)` is fixed and another point charge `q_(2)` is placed at a distance `r_(0)` from `q_(1)` on a frictionless horizontal surface.Find the velocity of `q_(2)` as a function of separation `r` between them (treat the changes as point charges and mass of `q_(2)` is m)
View SolutionA charge `+q_(0)` is fixed at a position in space. From a large distance another charged particle of charge -q and mass m is thrown towards `+q_(0)` with an impact parameter L as shown. The initial speed of the projected particle is v. Find the distance of closer approach of the two particles?

View SolutionA particle of mass 40 mg and carrying a charge `5 xx 10^(-9) C` is moving directly towards a fixed positive point charge on magnitude `10^(-8) C`. When it is at a distance of 10 cm from the fixed positive point charge it has a velocity of `50 cm s^(-1)` at what distance from the fixed point charge will the particle come momentarily to rest ? Is the acceleration constant during motion?
View SolutionA proton moves with a speed of `7.45xx10^(5)m//s` directly towards a free proton originally at rest.Find the distance of closest approach for the two protons. Given `(1//4pi epsilon_(0)_=9xx10^(9)m//s,m_(p)=1.67xx10^(-27)kg` and `e=1.6xx10^(-19)`coulomb.
View SolutionAn electron travelling from infinity with velocity `v` into an electric field due to two stationary electrons separated by a distance of `2m`.if it comes to rest when it reaches the mid point of the line joining the stationary electrons.The initial velocity `v` of the electron is
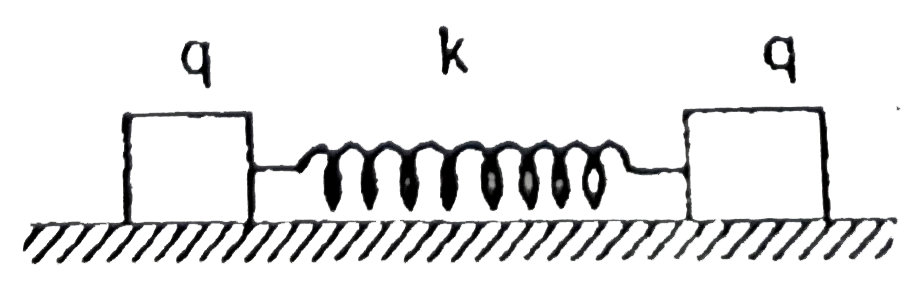
View SolutionTwo identical particles of charge `q` each are connected by a massless spring of force constant `k`. They are placed over a smooth horizontal surface. They are released when the separation between them is `r` and spring is unstretched. If maximum extension of the spring is `r`, the value of `k` is (neglect gravitational effect)
View SolutionIF an electron enters into a space between the plates of a parallel plate capacitor at an an angle `alpha` with the plates an leaves at an angle `beta` to the plates find the ratio of its kinetic energy while entering the capacitor of that while leaving.
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side `L`. The work done in increasing the side of the triangle to `2L` is
View SolutionDetermine the interaction enery of the point charge located at the corners of a square with the side a in the circuits shown in figure.

View SolutionTwo protons are separated by a distance R. What will be the speed of each proton when they reach infinity under their mutual repulsion?
View SolutionA bullet of mass `2 gm` is having a charge of `2 muc`. Through what potential difference must it be accelerated, starting from rest, to acquire a speed of `10 m//s`
View SolutionThree equal charges Q are at the vertices of an equilateral triangle of side A. How much work is done (by an external agent) in bringing them closer to an equilateral triangle of side A/2?
View SolutionTwo particles have equal masses of 5.0 g each and opposite charges of `+4.0 xx10^(-5) C.` They are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reducced to 50 cm.
View SolutionThe electric potential existing in space is `V(x,y,z)= A (xy+ yz+zx)`.(a) Write the dimensional A. (b) find the expression for the electric field.( c ) If A is 10 SI units, find the magnitude of the electric field at (1m, 1m, 1m).
View SolutionAn electric field `E = (20hati + 30 hatj)` N/C exists in the space. If thepotential at the origin is taken be zero, find the potential at `(2 m, 2 m)`.
View SolutionAn electric field `vecE = vec I Ax` exists in the space, where `A= 10 V m ^(-2).` Take the potential at (10m, 20m ) to be zero. Find the potential at the origin.
View SolutionA positively charged oil droplet remins stationary in the electric field between two horizontal plates separated by a distance of `1 cm` . The charge on the drop is `10^(-15) C` and mass of the droplet is `10^(-11) g`, the potential difference between the plates and if the polarity is reversed , the instantaneous of the droplet are
View SolutionAn oil drop 'B' has charge `1.6 xx 10^(-19)C and " mass " 1.6 xx 10^(-14)kg`. If the drop is in equilibrium position, then what will be potential difference between the plates. [The distance between the plates is 100mm]
View SolutionA, B, C, D, P, and Q are points in a uniform electric field. The potentials at these points are `V(A) = 2 V. V(P) = V( B) = V(D) = 5 V`, and `V(C) = 8 V`. Find the electric field at P.
 .
.
View SolutionThe electric potential V at any point x,y,z (all in metre) in space is given by `V=4x^2` volt. The electric field at the point `(1m, 0, 2m)` is ……………`V/m`.
View SolutionFind the potential difference `V_(AB)` between `A(2m, 1m, 0)` and `B(0, 2m, 4m)` in an electric field,
`E=(xhati-2yhatj+zhatk)V/m`
View SolutionFind the potential difference between points A and B in an electric field
`vec(E ) = (2hat(i) + 3hat(j) + 4hat(k)) NC^(-1)`
where `vec(r_(A)) = (hat(i) -2hat(j) + hat(k))m and vec(r_(B)) = (2hat(i) + hat(j) - 2hat(k))m`
View SolutionAn infinite plane sheet of charge density `10^(-8) Cm^(-2)` is held in air. In this situation how far apart are two equipotenitial surfaces, whose p.d is 5 V ?
View SolutionA unifrom field of magnitude 2000 N/C is directed `37^(@)` below the horizontal as shown in the figure . Find (a) the potenital differenc between P and R. (b) If we define the reference level of potential so that potential at R is 500 V, what is the potential at P ?

View SolutionElectric field intensity at a point B due to a point charge Q kept at point A is `24 NC^(-1)`, and electric potential at B due to the same charge is `12 JC^(-1)`. Calculate the distance `AB` and magnitude of charge.
View SolutionThe electric field in a region is given by `vecE = (A/x^3) vecI.` Write a suitable SI unit for A. Write an experssion for. the potential in the region assuming the potential at. infinity to be zero.
View SolutionTwo point charges ` - 5 mu C` and ` + 3 muC` are placed 64 cm apart . At what points on the line joining the two charges is the electric potential zero ? (Assume the potential at infinity to be zero) .
View SolutionAn electirc dipole consists of two charges of equal magnitude and opposite sign separated by a distance 2a , as shown in figure . The diople is along the x-axis and is centered at the orgin.

(A) Calculate the electric potential at point P .
(B) Calculate V at point far from the dipole.
View SolutionWhen an electric dipole is placed in a uniform electric field making angle `theta` with electric field, it experiences a torque `tau`. Calculate the minimum work donein changing the orientation to `2 theta`.
View SolutionA molecule of a substance has a permanent electric dipole moment of magnitude `10^(-29) `C m. A mole of this substance is polarized at low temperature by appling a strong elecrostatic field of magnitude `10^(6) V m^(-1)`. The direction of the field is suddenly changed by an angle of `60^(@)`. Estimate the heat released by the substance in aligning its dipole along the new direction of the field. For simplicity, assume `100%` polarisation of sample.
View SolutionAn electric dipole in a uniform electric field E is turned form ` theta = 0` position to ` theta = 60^(@)`
position . Find work done by the field .
View SolutionAn electric dipole of dipole moment p is kept at a distance r form infinite long charged wire of linear charge denisty ` lambda` as shown . Find the force acting on the dipole ?

View SolutionA charge Q is distributed over two concentric hollow spheres of radii r and `R (gt r)` such that the surface charge densities are equal. Find the potential at the common centre.
View SolutionFigure shows two conectric conducting shell of radii , `r_(1)` and `r_(2)` carrying uniformly distributed charages `q_(1)` and `q_(2)` . Respectively . Find out an expression for the potential of each shell.

View SolutionIn the previous example, if the charge `q_(1) = + q_(0)` and no charge an outer shell. The outer shell is earthed , then
(a) determine the charge on the outer shell, and
(b) find the potential of the inner shell .

View SolutionConsider two concentric spherical metal shells fo radii 'a' and `b gt a`. The outer shell has charge Q, but the inner shell has no charge , Now the inner shell is grounded. This means that the inner shell will come at zero potential and that electric field lines leave the outer shell an end on the inner shell .
(a) Find the charge on the inner shell .
(b) Find the potential on outer sphere.

View SolutionTwo circular loops of radii 0.05 and 0.09m, respectively , are put such that their axes coincide and their centre are 0.12 m apart. Charge of `10^(-6)` coulomb is spread uniformly on each loop. Find the potential difference between the centres of loops.

View SolutionA circular ring of radius R with uniform positive charge density `lambda` per unit length is loacted in the y - z plane with its centre at the origin O . A particle of mass 'm' and positive charge 'q' is projected form the point ` p [ - sqrt(3)R,00]` on the negative x - axis directly towards O , with initial speed V. Find the smallest (non - zero) value of the speed such that the particle does not return to P ?

View SolutionA charge of` +2.0xx 10 ^-8 C` is placed on the positive place and a charge of -`1.0 xx 10 ^-8 C` on the negative plate of a parallel- plate capacitor of capacitance ` 1.2 xx (10^-3) mu` F. Calculate the potential difference developed between the plates.
View SolutionA capacitor of capacitance C is charged by connecting it to a battery of emf epsilon. The capacitor is now disconnected and reconnected to the battery with the polarity reversed. Calculate the heat developed in the connecting wires.
View SolutionA parallel plate air capacitor is made using two plates 0.2 m square , spaced 1 cm apart . It is connected to a 50V battery.
(a) what is the capacitance ?
(b) what is the charge one each plane ?
(c) what is energy stored in the capacitor ?
(d) what is the electric field between the plates ?
(e) If the battery is disconnected and then the plates are pulled apart to a separation of 2 cm , what are the answer to the above parts ?
View SolutionFigure shows two capacitors connected in series and joined to a battery . Draw the graph showing the variation in potential as one moves form left to ring on the branch containing the capacitors. Take `C_(1) gt C_(2)`

View SolutionA capacitor is made of a flat plate of area A and a second plate having a stair - like structure as shown in figure. The width fo each stair is a and the height is b. Find the capacitance of the assembly.

View SolutionTwo capacitors of capacitance 20.0 pF and 50.0 pF are connected is series with a battery of 20 V. Find the energy supplied by the battery.
View SolutionEach capacitor shown in figure has a capacitance of `6.0 mu F` . The emf fo the battery is 50 v. How much charge will flow through AB if the switch S is closed ?

View SolutionA capaitor of capacitance `C_(1) = 1.0 muF` withstands teh maximum voltage `V_(1) = 6.0 kV` while a capacitor of capacitance `C_(s) = 2.0 muF`, the maximum voltage `V_(s) = 4.0 kV`. What voltage will the system of these two capacitors withsatand if they are connected in sereis ?
View SolutionFind the p.d between the point A and B in the fig. The value of capacitance are in `mu F`.

View SolutionFind the equivalent capacitance between points A and B for the following figs . Assume that each plate has surface area A and the separation between the two consective plates is s.

View SolutionA capacitor is composed of two plates separated by a sheet of insulating material 13 mm thick and or relative permittivity 4. The distance between the plates is increased to allow the insertion of second sheet 5 mm thick and of relative permittivity `in_(r)`. If the capacitance of the capacitor so formed is 1/3 of the original capacitance , find `in_(r)`.
View SolutionThe parallel plate of a capacitor have an area `0.2 m^(2)` and are `10^(-2)` m apart. The original potential difference between them is 3000V, and it decreases to 1000 when a sheet of dielectric is inserted between the plates. Compute
(a) Original capacitance `C_(0)`
(b) The original charge Q on each plate .
(C) Capacitance C after insertion of the dielectric .
(d) Dielectric constant K .
(e) The original field `E_(0)` between the plates and .
(f) The electric field `E_(0)` between the plates and .
(f) The electric field E after insertion of the dielectric . `(epsi_(0) = 8.85 xx 10^(-12) S.I` unit).
View Solution
Illustration questions and complete solutions for chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of NARAYANA PHYSICS (HINGLISH) of Class 12
All Exercises from NARAYANA Class 12 PHYSICS ELECTROSTATIC POTENTIAL AND CAPACITANCE
- ADDITIONAL PROBLEMS
- C.U.Q (Capacitors and Capacitance)
- C.U.Q (Electrostatics of conductors)
- C.U.Q (Potential and Potential Difference)
- C.U.Q (Potential due to continuous charge distribution)
- C.U.Q (Potential energy of dipole)
- C.U.Q (Potential energy of system of charges )
- C.U.Q (Van De Graff Generator )
- Evaluate yourself-1
- Evaluate yourself-10
- Evaluate yourself-2
- Evaluate yourself-3
- Evaluate yourself-4
- Evaluate yourself-5
- Evaluate yourself-6
- Evaluate yourself-7
- Evaluate yourself-8
- Evaluate yourself-9
- EXERCISE - 3 (PREVIOUS AIPMT QUESTIONS)
- EXERCISE - 4 (NCERT EXAMPLAR PROBLEMS)
- Exercise -1 (C.W)
- Exercise -1 (H.W)
- EXERCISE -2 (H.W)
- Exercise-2(C.W)
- Illustration