Complete Solutions to Examples of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| NARAYANA | Examples |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
In a hydrogen atom, electron moves in an orbit of radius `5xx10^(-11)m` with a speed of `2.2xx10^(6)(m)/(s)`. Calculate the equivalent current.
View SolutionThe current through a wire depends on time as
`I = i_(0) + alphat`,
where `i_(0)=10 A and alpha=4 As^(-1)`.Find the charge crossed through a section of the wire in 10 second
View SolutionConsider a wire of length 4m and cross-sectional areal `1 mm^(2)` carrying of 2A. If each cubic metre of the material contains `10^(29)`free electrons, find the average time taken by an electron to cross the length of the wire.
View SolutionA rectangular block has dimensions `5cmxx5cmxx10cm`. Calculate the resistance measured between (a) two square ends and (b) the opposite rectangular ends. Specific resistance of the material is `3.5xx10^(-5)Omegam`.
View SolutionTemperature coefficient of resistance of platinum is `alpha=3.92xx10^(-3)K^(-1)` at `0^(@)C`. Find the temperature at which the increase in the resistance of platinum wire is `10%` of its value at `0^(@)C`
View SolutionThe resistance of iron wire is `10Omega` and `alpha=5xx(10^(-3))/( .^(@)C)`. If a current of 30A is flowing in it at `20^(@)C` keeping the potential difference across its length constant, if the temperature is incresed to `120^(@)C` what is the current flowing through that wire?
View SolutionResistance of a resistor at temperature `t^@C` is `R_t =R_0 (1+alphat + betat^2)`, where `R_0` is the resistance at `0^@C`. The temperature coefficient of resistance at temperature `t^@C` is
View SolutionA silver wire has a resistance of `2.1Omega` at `27.5^(@)C&2.7Omega` at `100^(@)C` Determine the temperature coefficient of resistivity of silver.
View Solution`V-i` graphs of anichrome wire at three different temeperatures `t_(1)`, `t_(2)` and `t_(3)` are shown. From the graph.
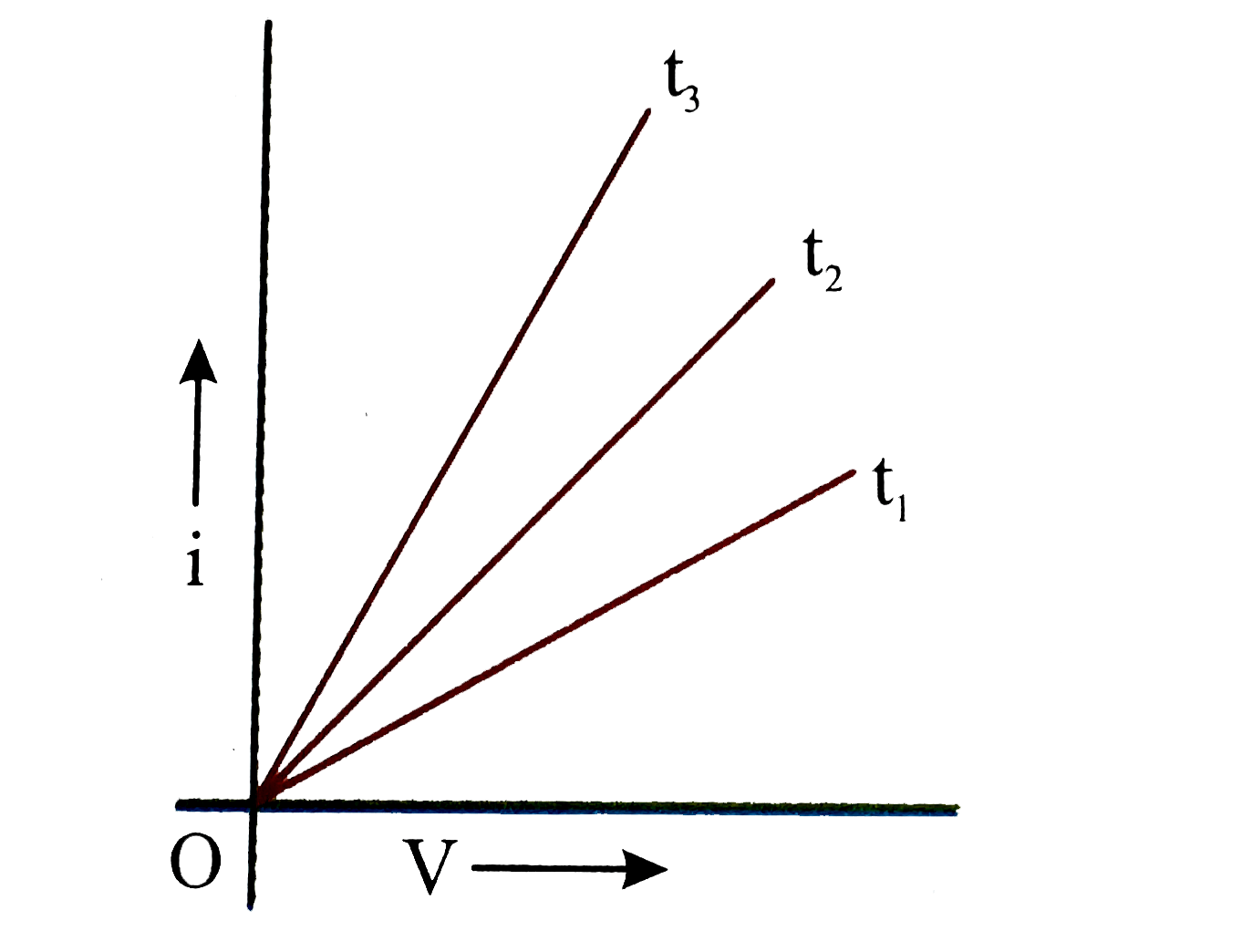
View SolutionShown a conductor of length `l` having a circular cross section. The radius of cross section varies linearly form `a to b`. The resistivity of the material is`(rho)`.Assuming that `b-altltl`,find the resistance of the conductor.

View SolutionA hollow cylinder of specific resistance `rho`, inner radius `R`, outer radius `2R` and length 1 is as shown in figure. What is the net resistance between the inner and outer surfaces?
View SolutionThere are two concentric spheres of radius a and b respectively. If the space between them is filled with medium of resistivity `rho`, then the resistance of the intergap between the two spheres will be (Assume `bgta`)
View SolutionA hollow copper cylinder is of inner radius 4 cm outer radius 5 cm. Now hollow portion is completely filled with suitable copper wires. Find percentage change in its electric resistance.
View SolutionResistivity of the material of a conductor of uniform cross-section varies along its length as `rho=rho_(0)(1+alpha x)`. Find its resistance if its length is L and area of cross-section is A.
View SolutionHow many number of turns of nichrome wire of specific resistance `10^(-6)Omegam` and diameter 2mm that should be wound on a cylinder of diameter 5 cm to obtain a resistance of `40Omega`?
View SolutionThe four colours on a resistor are: brown, yellow, green and gold as read from left to right. What is resistance corresponding to these colours.
View SolutionFor a circuit shown in fig find the value of resistance `R_(2)` and current `I_(2)` flowing thorugh `R_(2)`
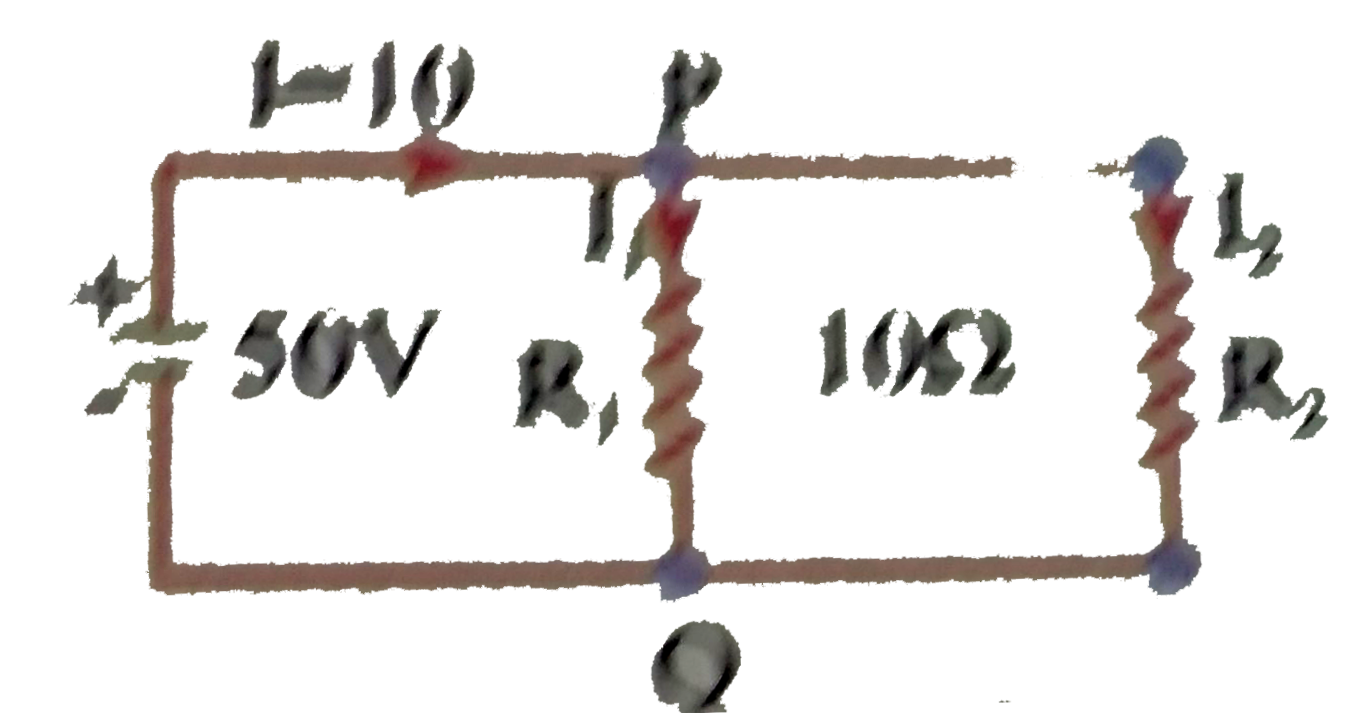
View SolutionTwo wires of equal diameters of resistivities `rho_(1)` and `rho_(2)` and length `x_(1)` and `x_(2)` respectively are joined in series. Find the equivalent resistivity of the combination.
View Solution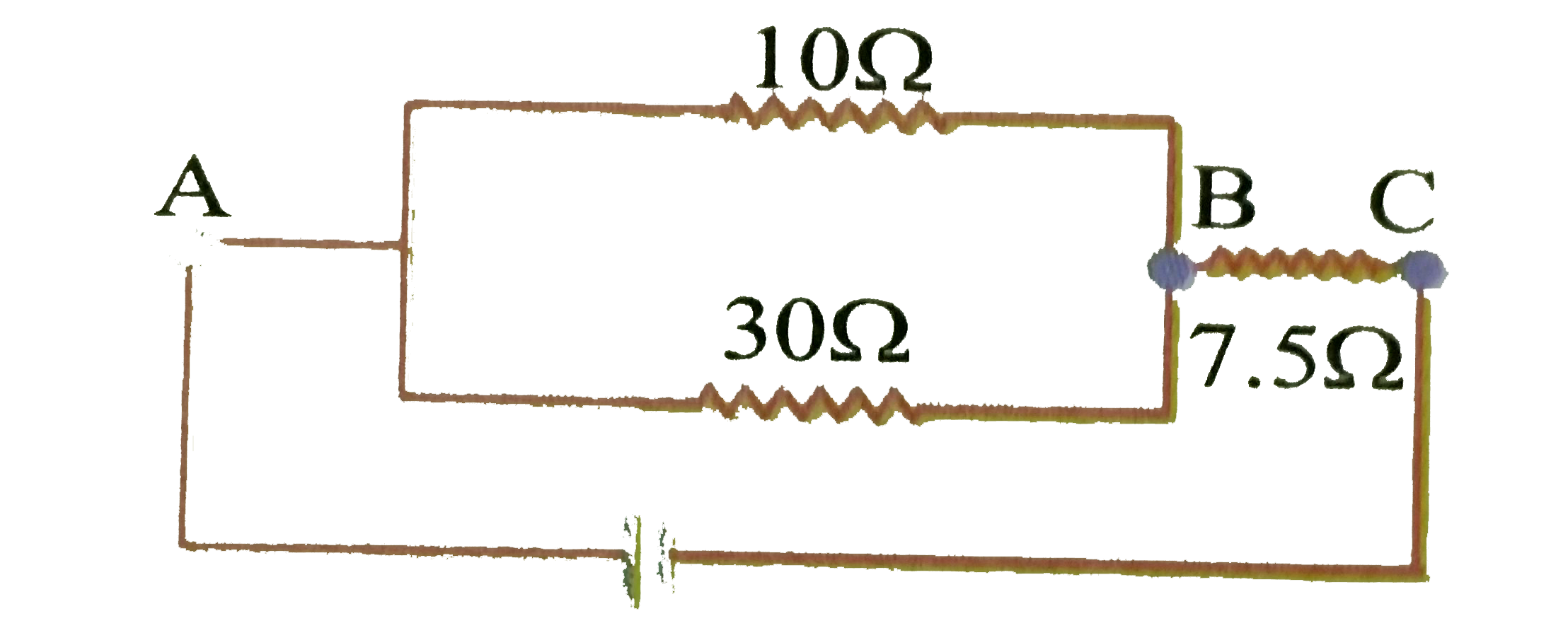
Find equivalent resistance of the network in fig. Between points (i) A and B and (ii) A and C.
View Solution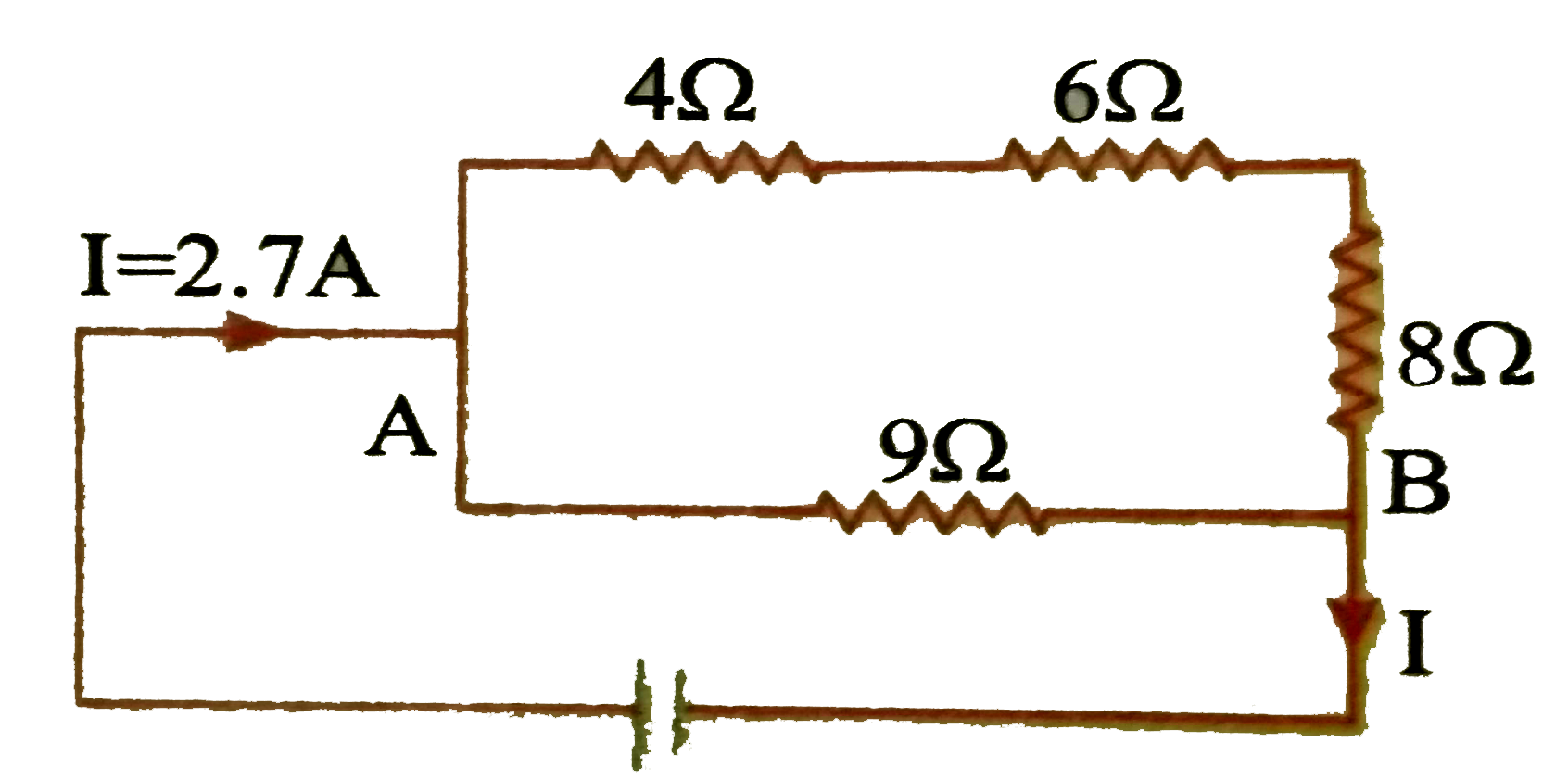
Find potential difference between points A and B of the network shown in fig. and distribution of given main current through different resistors.
View SolutionIn a uniform ring of resistance `R` there are two points `A` and `B` such that `/_ ACB = theta`, where `C` is the centre of the ring. The equivalent resistance between `A` and `B` is
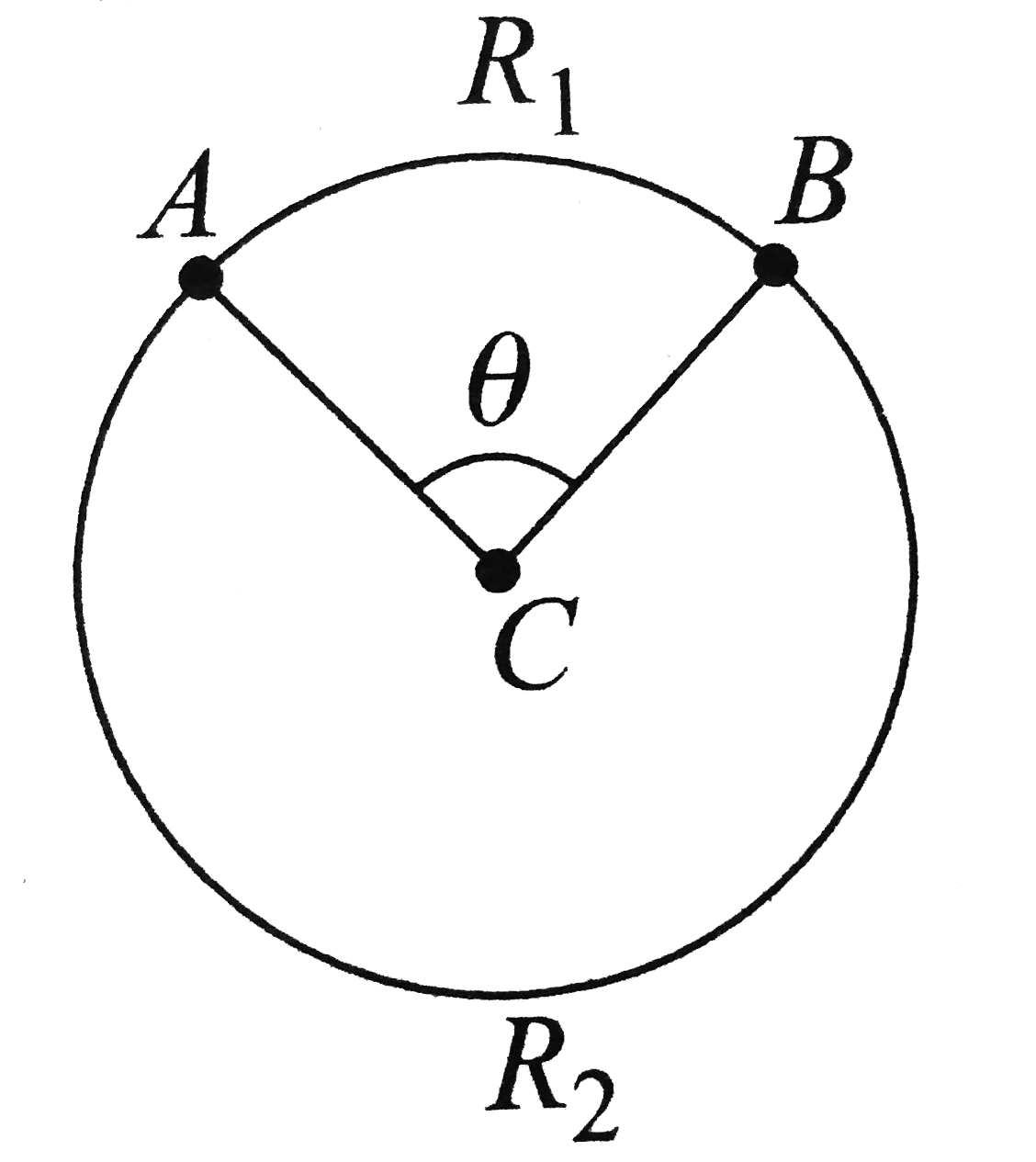
View Solution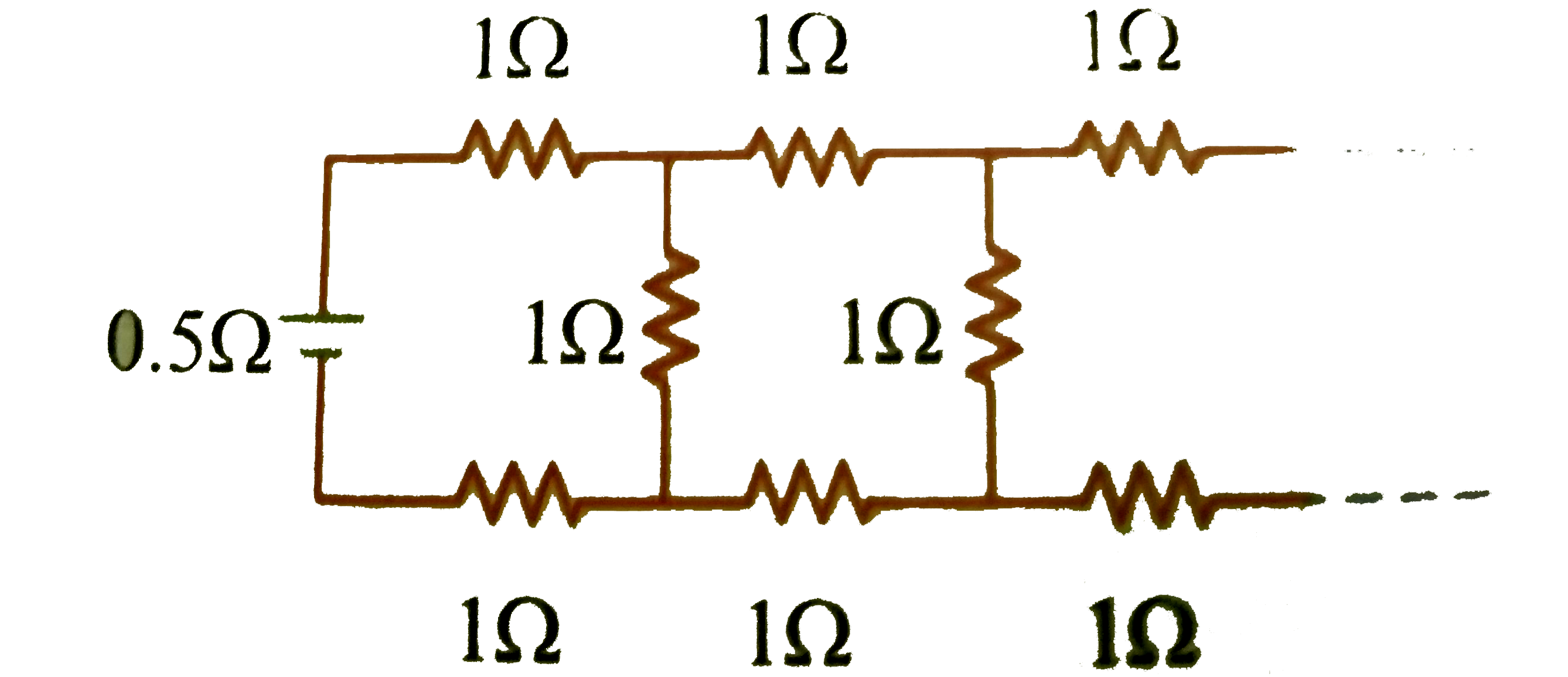
Determine the current drawn from a `12V` supply with internal resistance `0.5Omega`. By the infinite network shown in fig. Each resistor has `1Omega` resistance.
View SolutionA fuse wire with radius of `0.2mm` blows off with a current of 5 Amp. The fuse wire of same material,but of radius 0.3 mm will blow off with a current of
(1) `5xx(3)/(2)Amp`
(2). `(5sqrt(3))/(2)Amp`
(3). `5sqrt((27)/(8))Amp`
(4). `5 Amp`
View SolutionA 1 kQ heater is meant to operate at 200 V. (a) what is its resistance ? (b) How much power will it consume if the line voltage drops to 100 V? (c) how many units of electrical energy will it consume in a month (of 30 days) if it operates 10 hr daily at the specified voltage?
View SolutionA lamp of 100 W works at 220 volts What is its resistance and current capacity?
View SolutionA `100W-220V` bulb is connected to 110 V source. Calculate the power consumed by the bulb.
View SolutionA `100W` and a `500W` bulbs are joined in series and connected to the mains which bulb will glow brighter?
View SolutionA cell develops the same power across two resistances `R_(1)` and `R_(2)` separately. The internal resistance of the cell is
View Solution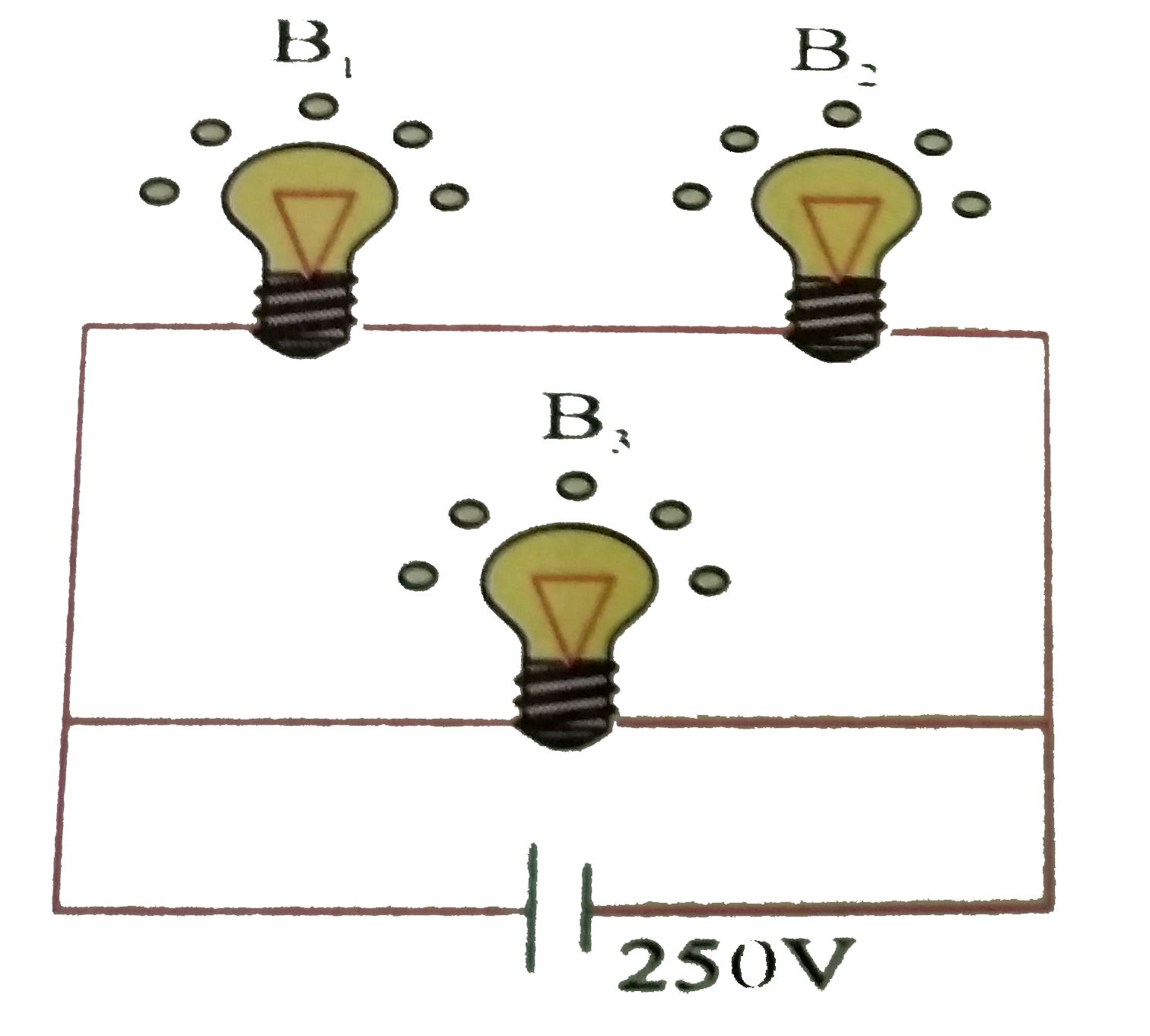
A 100 W bulb `B_(1)` and two 60 W bulbs `B_(2)` and `B_(3)`, are connected to a 250V source, as shown in the figure now `W_(1),W_(2)` and `W_(3)` are the output powers of the bulbs `B_(1),B_(2)` and `B_(3)` respectively then
View Solution
A battery if internal resistance `4Omega` is conneted to the network of resistances as shown. What must be the value of R so that maximum power is delivered to the network Find the maximum power?
View SolutionWhen a current drawn from a battery is 0.5 A its terminal potential difference is 20 V. And when current drawn from it is 2.0 A, the terminal voltage reduces to 16 V. Find out. `e.m.f` and internal resistance of the bettery.
View SolutionAn ideal battery sends a current of 5A in a resistor.When another resistor of value `10 Omega`is connected in parallel ,the current through the battery is increased to 6A.Find the resistance of the first resistor.
View SolutionWhen a bettery is connected to the resistance of `10Omega` the current in the circuit is 0.12 A the same battery gives `0.07A` current with `20Omega` calculate `e.m.f` and internal resistance of the battery.
View SolutionTwo cells `A` and `B` with same `e.m.f` of 2 V each and with internal resistances `r_(A)=3.5Omega` and `r_(B)=0.5Omega` are connected in series with an external resistance `R=3Omega` Find the terminal voltages across the two cells.
View SolutionTwo cells `A` and `B` each of 2 V are connected in series to an external resistance `R=1` ohm.The internal resistance of A is `r_(A)=1.9` ohm and B is `r_(B)=0.9` ohm. Find the potential difference between the terminals of `A`.
View Solution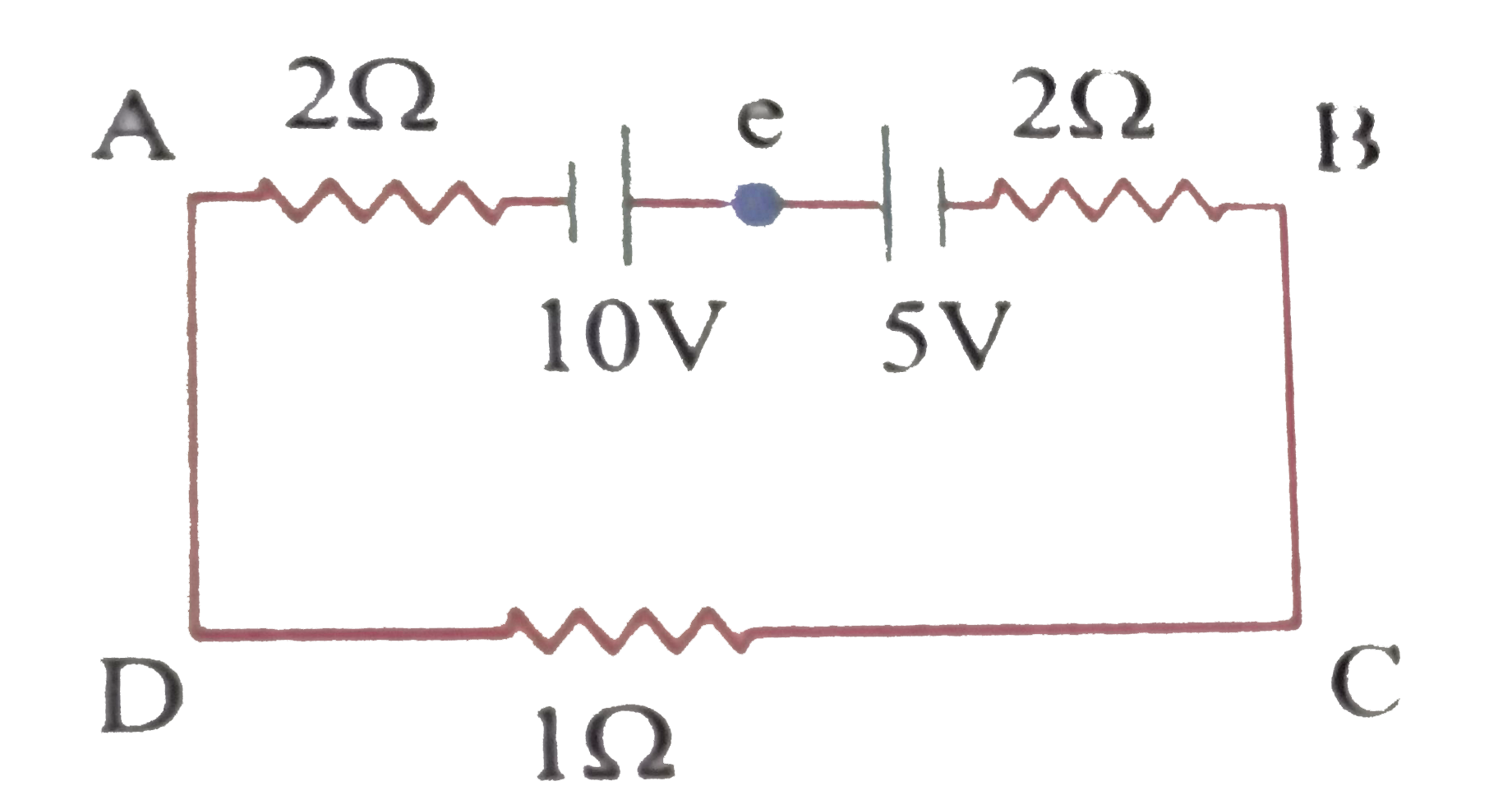
In the given circuit as shown below calculate the magnitude and direction of the current
View SolutionA voltmeter with resistance `500 Omega` is used to measure the emf of a cell of internal resistance `4 Omega`. The percentage error in the reading of the voltmeter will be
View SolutionFind the emf (`V`) and internal resistance `(R)` of a single battery which is equivalent toa parallel combination of two batteries of emf `V_1` and `V_2` and internal resistances `r_1` and `r_2` respectively, with polrities as shown in figure

View Solution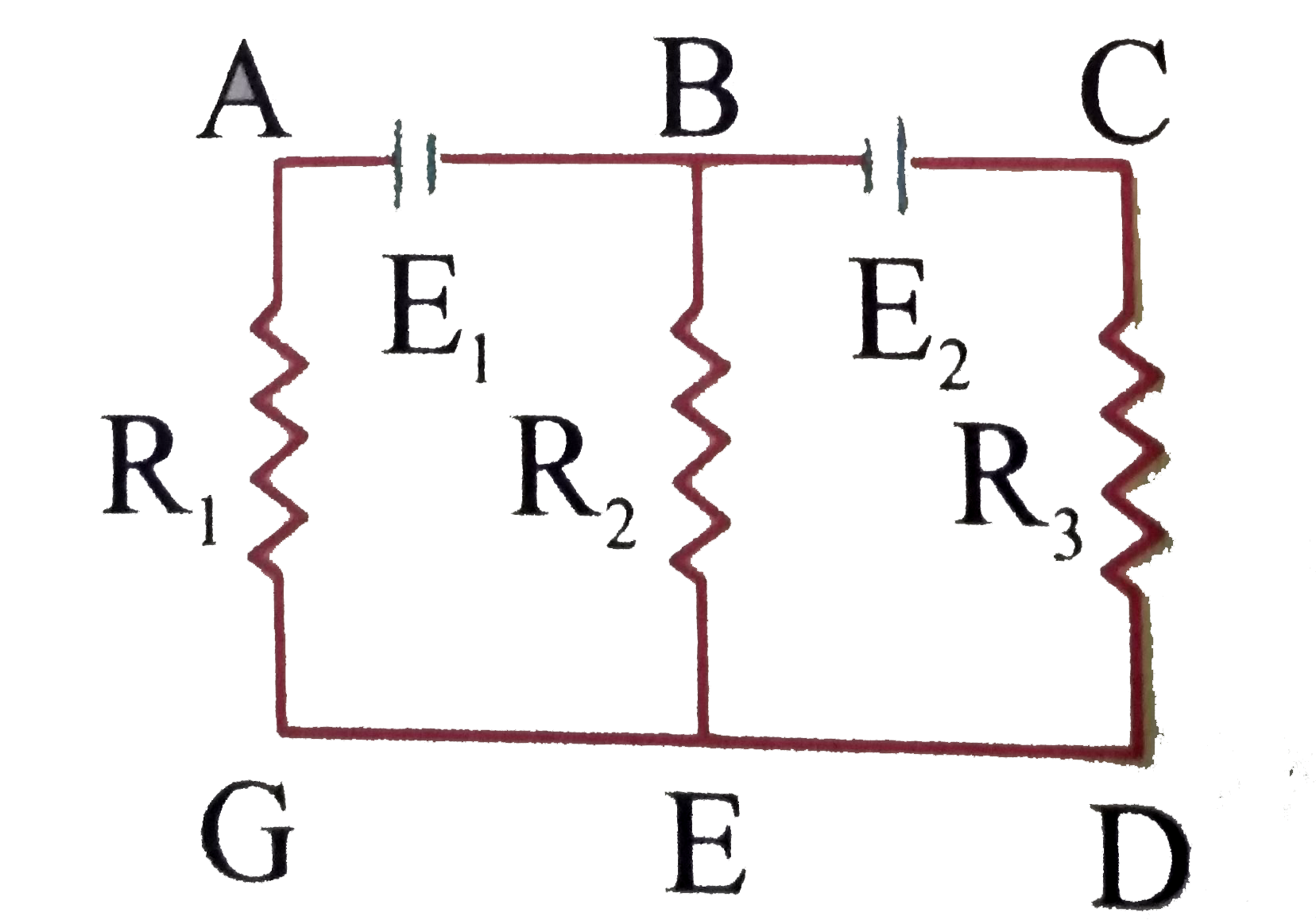
In the given circuit values are as follows
`epsi=2V,epsi_(2)=4V,R_(1)=1Omega` and `R_(2)=R_(3)=1Omega`.
Calculate the current through `R_(1),R_(2)` and `R_(3)`
View Solution
Solve for current values in figure.
View Solution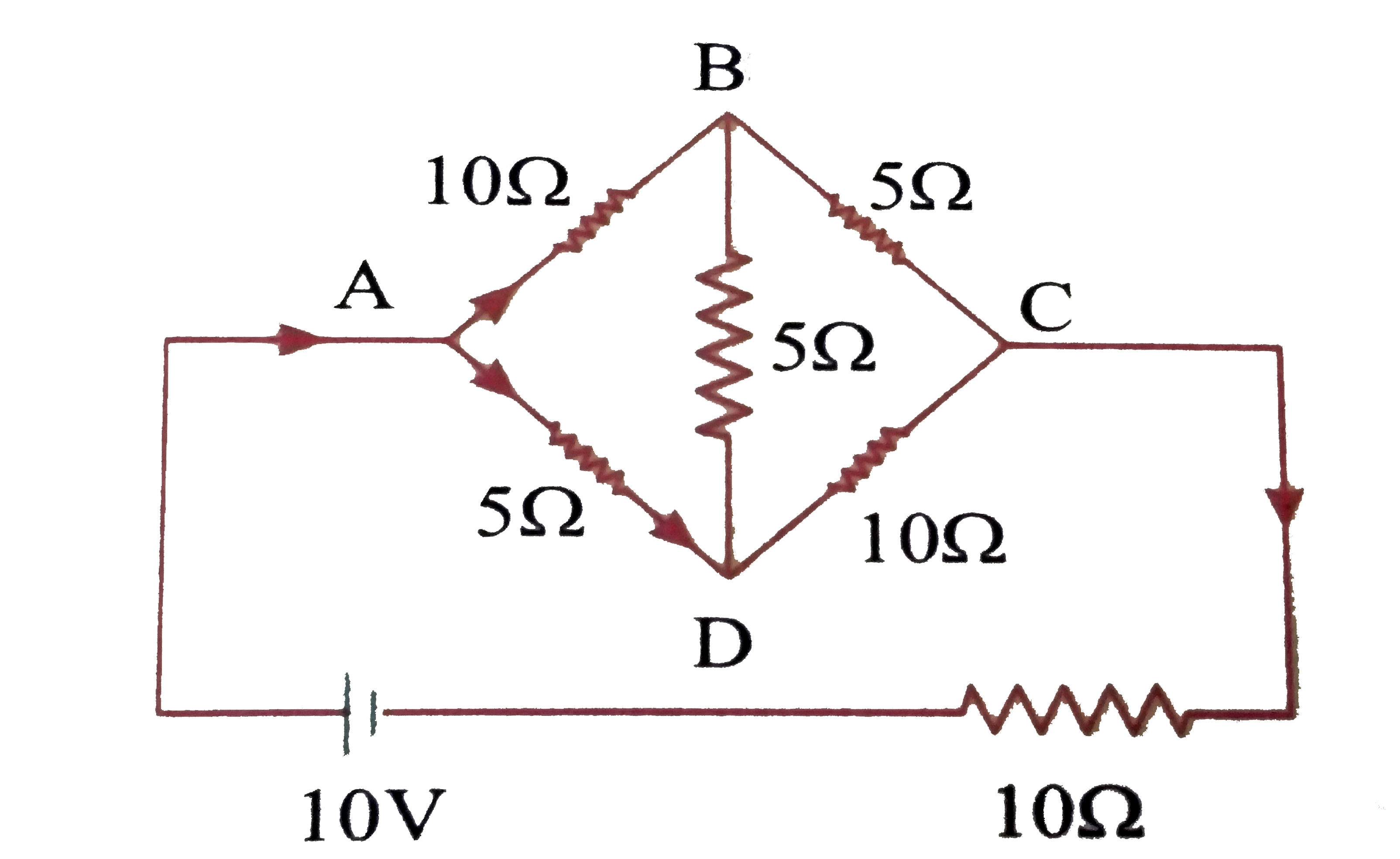
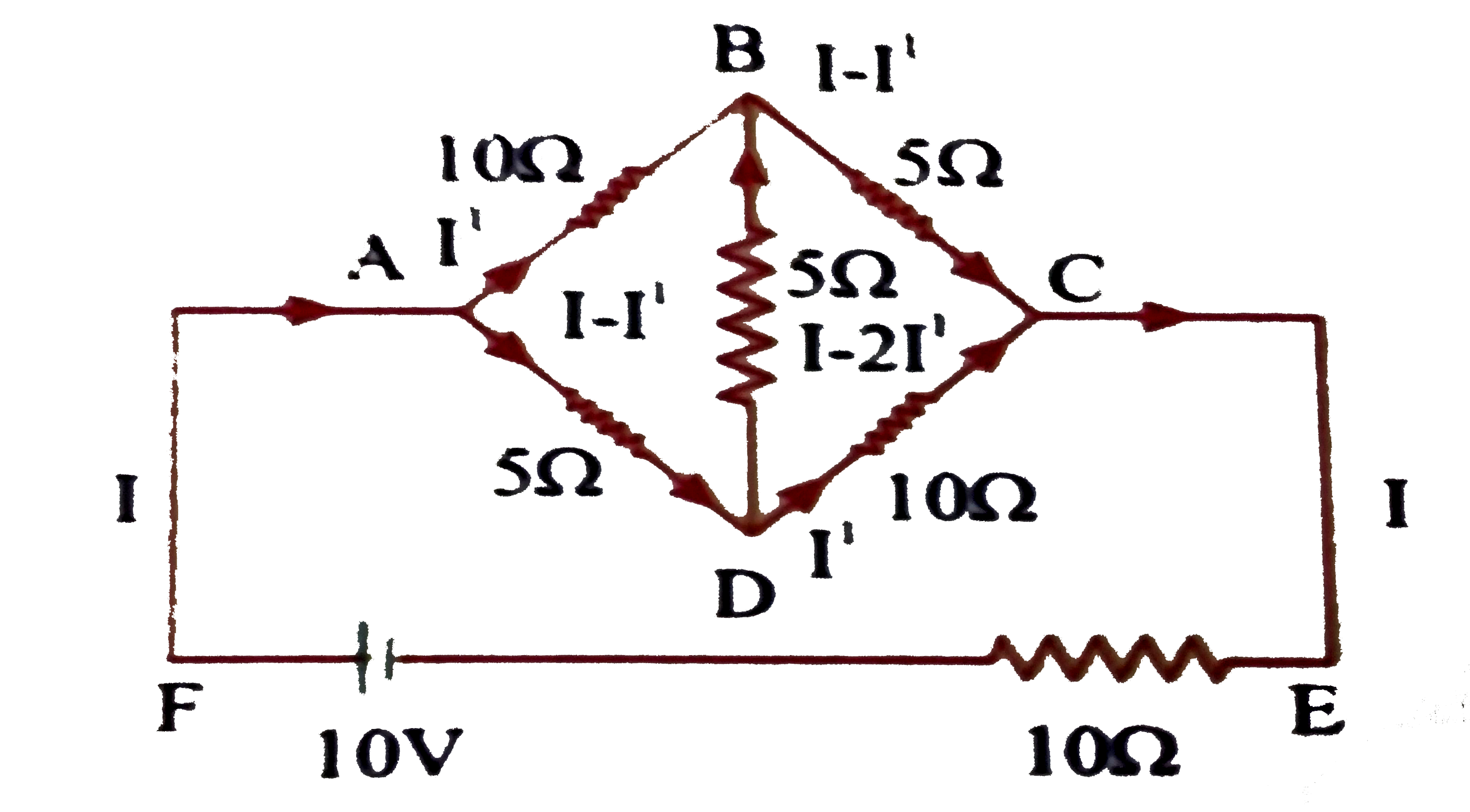
Determine the current in each branch of the network shown in fig.
View SolutionIn the shown arrangement of the experiment of the meter bridge if AC corroesponding to null deflection of galvanometer is x, what would be its value if the radius of the wire AB is doubled?
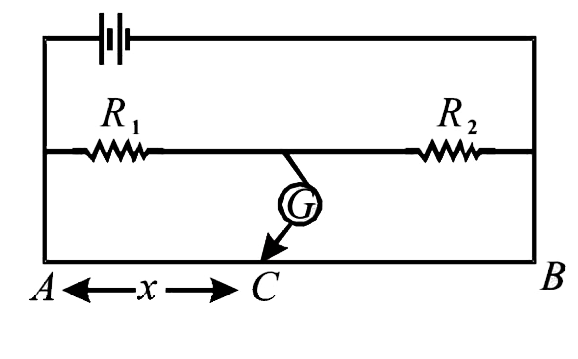 .
.
View SolutionA resistance of `2Omega` is connected across one gap of a meter bridge (the length of the wire is `100 cm`) and an unknown resistance, greater than `2Omega`is conneted across the other gap. When these resistances are interchanged, the balance point shifts by `20 cm`. Neglecting any corrections,the unknown resistance is
View SolutionThe length of a potentiometer wire is 1m and its resistance is `4Omega` A current of 5 mA is flowing in it. An unknown source of emf is balanced on 40 cm length of this wire, then find the emf of the source.
View SolutionA cell of emf 2 volt and internal resistance `1.5Omega` is connected to the ends of 1 long wire. The resistance of wire is (0.5Omega)/(m)`. Find the value of potential gradient on the wire.
View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of `10Omega` is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View SolutionIn a potentiometer experiment when a battery of emf 2V is included in the secondary circuit the balance point is 500 cm. Find the balancing length of the same end when a cadimum cell of emf 1.018V is connected to the secondary circuit.
View Solution
Examples questions and complete solutions for chapter CURRENT ELECTRICITY of NARAYANA PHYSICS (HINGLISH) of Class 12