Complete Solutions to Solved Examples of chapter CIRCLE of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLE |
| NAGEEN PRAKASHAN | Solved Examples |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
In the adjoining figure `angle QPO=25^(@)` and `angle SPR = 20^(@)` , find the value of `angle QOR`.

View SolutionIn the adjoining figure `O` is the centre of the circle . If chord `AB=2` cm radius `OA=2` cm, then find the value of `angle ACB`.

View SolutionIn the adjoining figure , `O` is the centre of the circle and `angleOAB=60^(@)`. Find `angle APC`.

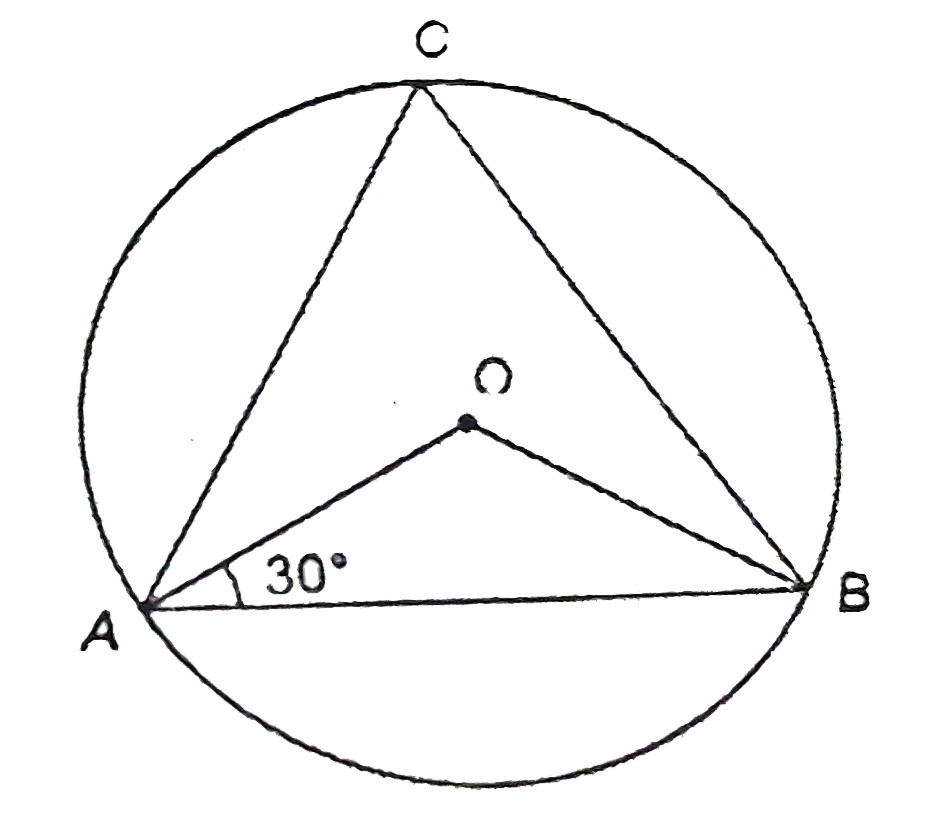
View SolutionIn the adjoining , `O` is the centre of the circle. `ACB` is a segment. If `angle OAB=30^(@)`, then find the value of `angle ACB`.
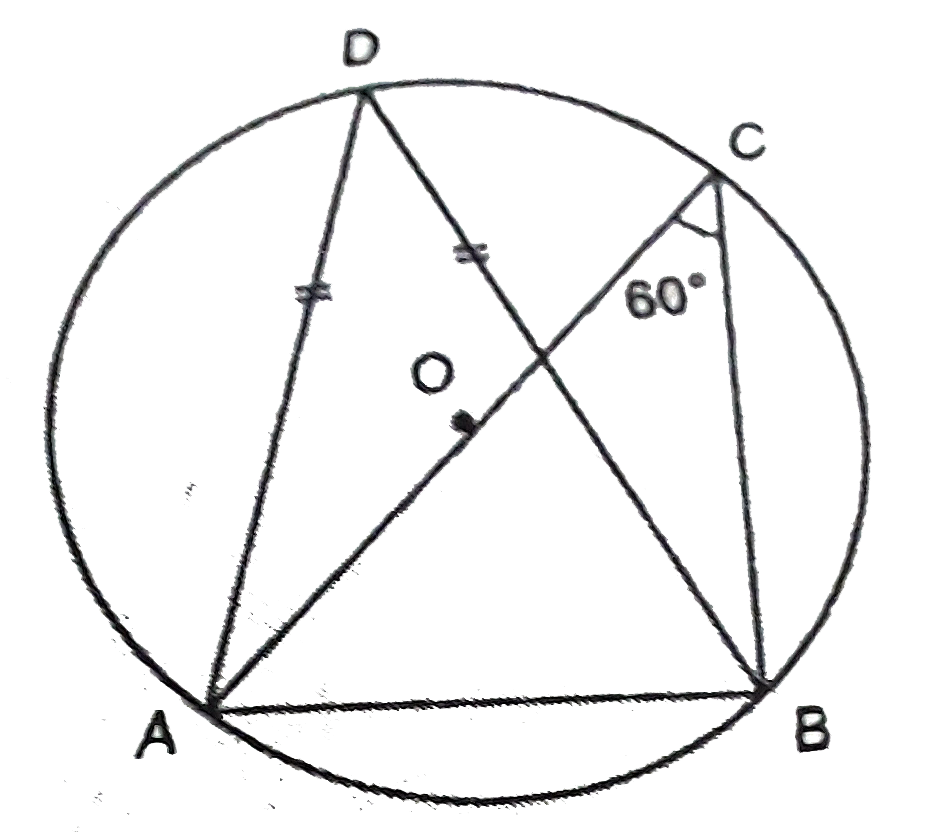
View SolutionIn the following figure `O` is the centre of the circel. If `angleACB=60^(@)` and `DA=DB` then prove that `DeltaADB` is an equilateral triangle.
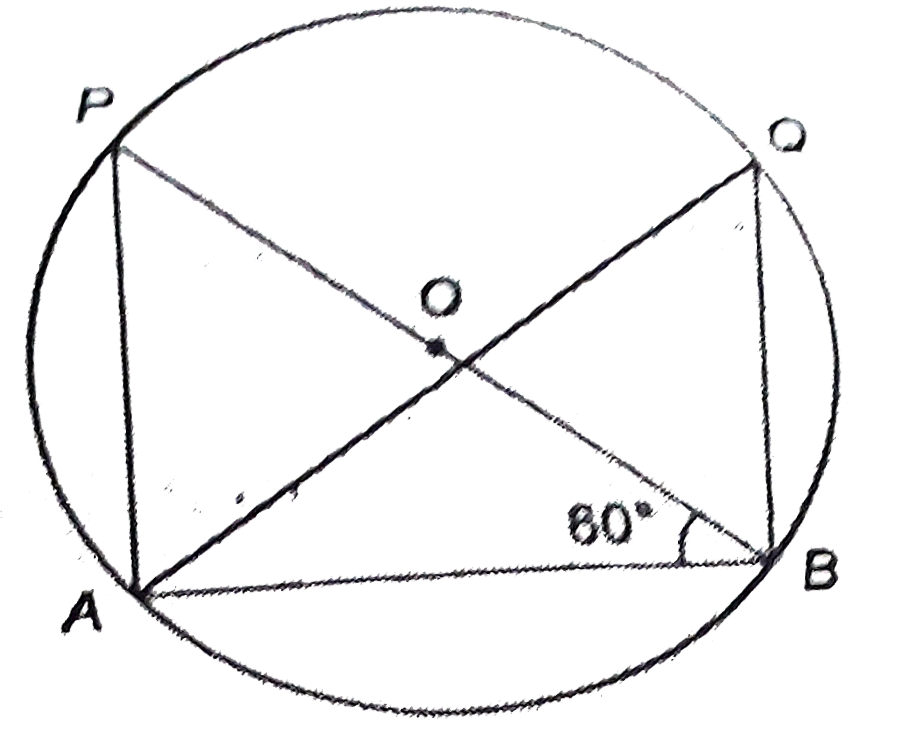
View SolutionIn the adjoining figure, BP is the diameter of the circle. If `angle ABP=60^(@)`, then find `angle AQB`.
View SolutionIn the figure, two circles intersect each other at points `A` and `B`. `AP` and `AQ` are the diameters of these circles. Prove that `PBQ` is a straight line.

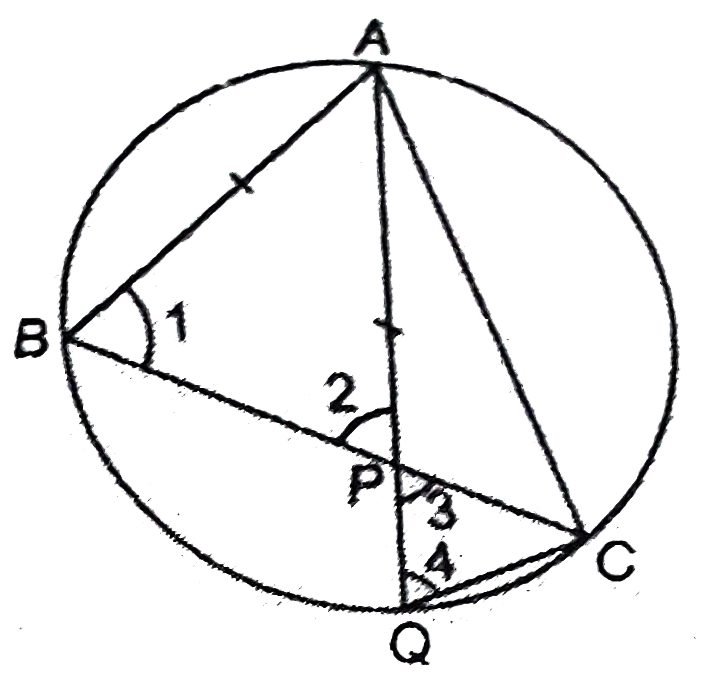
View SolutionIn given figure, `ABC` is a triangle produced meets the circumcircle of `Delta ABC` at `Q`, prove that `CP=CQ`
View Solution`D` is a point on the circumcircle of `Delta ABC` in which `AB=AC` such that `B` and `D` are on opposite sides of line `AC`. If `CD` is produced to a point `E` such that `CE=BD`, prove that `AD=AE`.
View SolutionIn the figure, `P` is the centre of the circle. Prove that : `angle XPZ=2(angleXZY+angleYXZ)`.

View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
View SolutionIn a circel with centre O. chords AB and CD interest inside the circumference at E. Prove that `angle AOC+BOD=2angle AEC`.
View SolutionIn figure O is the centre of the circle, prove that `anglez=anglex+angley`.

View SolutionThe diagonals `AC` and `BD` of a cyclic quadrilateral `ABCD` interest at right angles at E (figure). A line l drawn through E and perpendicular to AB meets CD at F. Prove that F is the mid-point of CD.
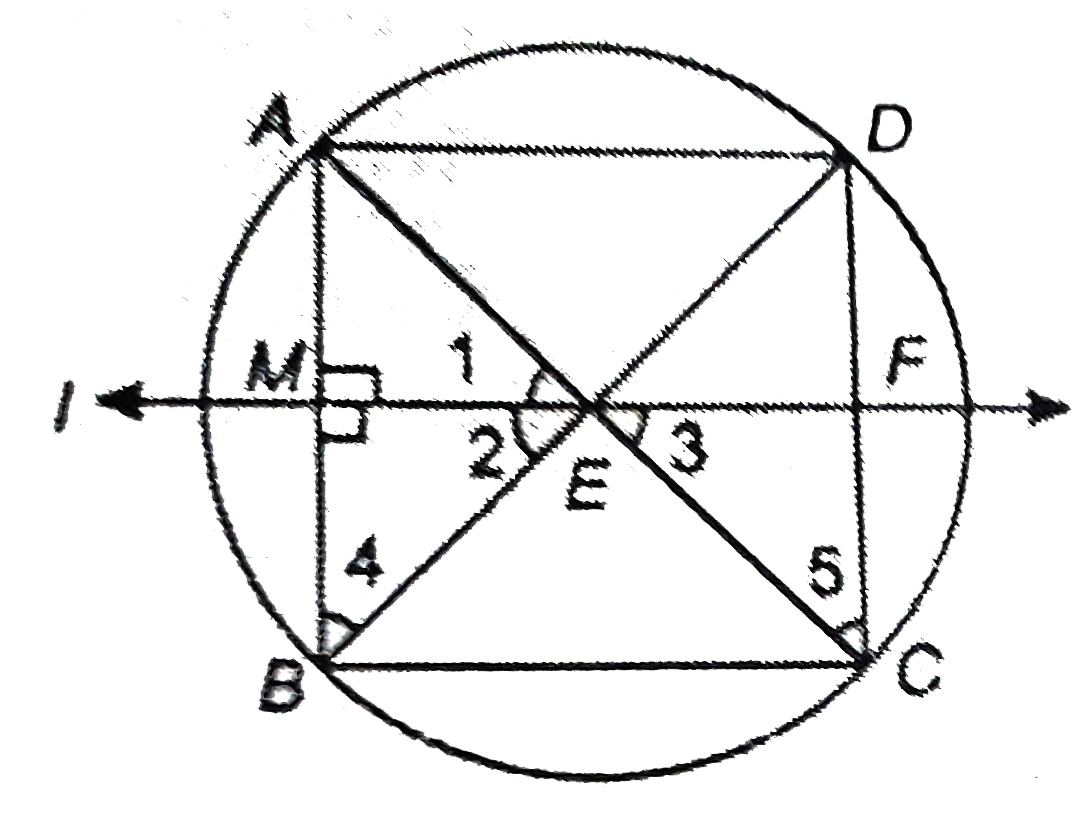
View SolutionAB is a diameter of the circle with centre `O` and chord `CD` is equal to radius `OC` (fig). `AC` and `BD` proudced meet at P. Prove that `angle CPD=60^(@)`.
View SolutionIn given fig., if `(x)/(3)=(y)/(4)=(z)/(5)` , then calculate the values of x,y and z.
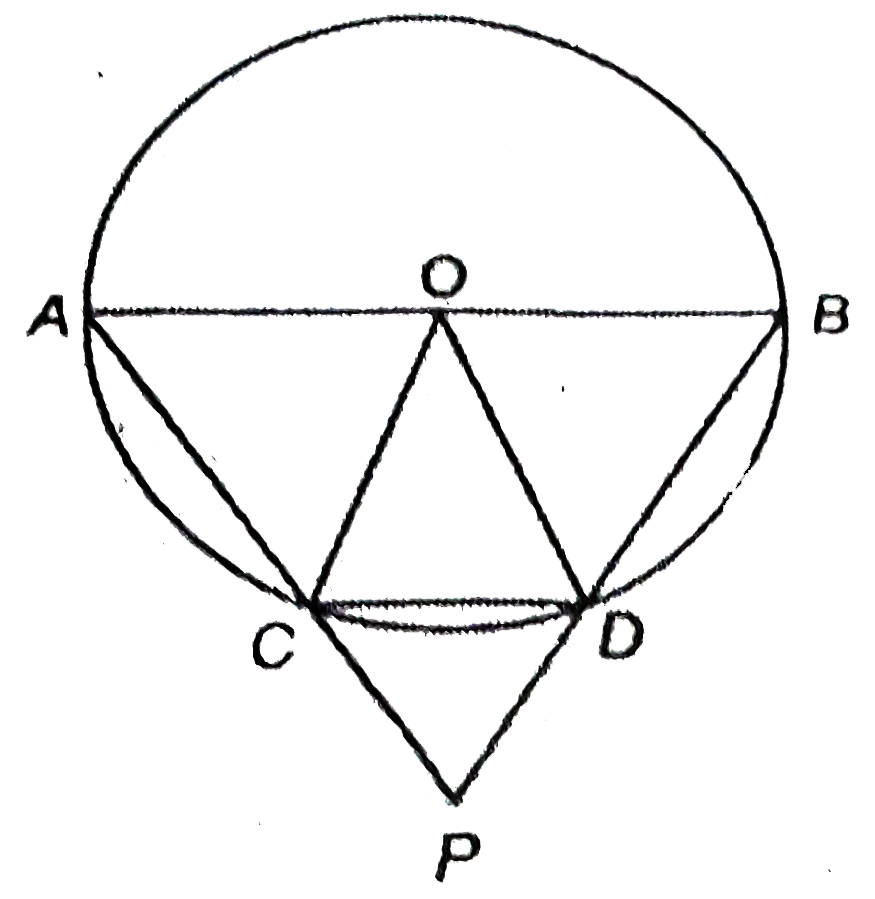
View SolutionProve that any four vertices of a regular pentagon are concyclic.
View SolutionIn figure O is the centre of the circle, prove that `anglez=anglex+angley`.

View SolutionTwo chords PQ and QR are equildistant form `O` the centre of the circle. If QS, is the diameter, then show that QS bisects `angle PQR` and `anglePSR`.
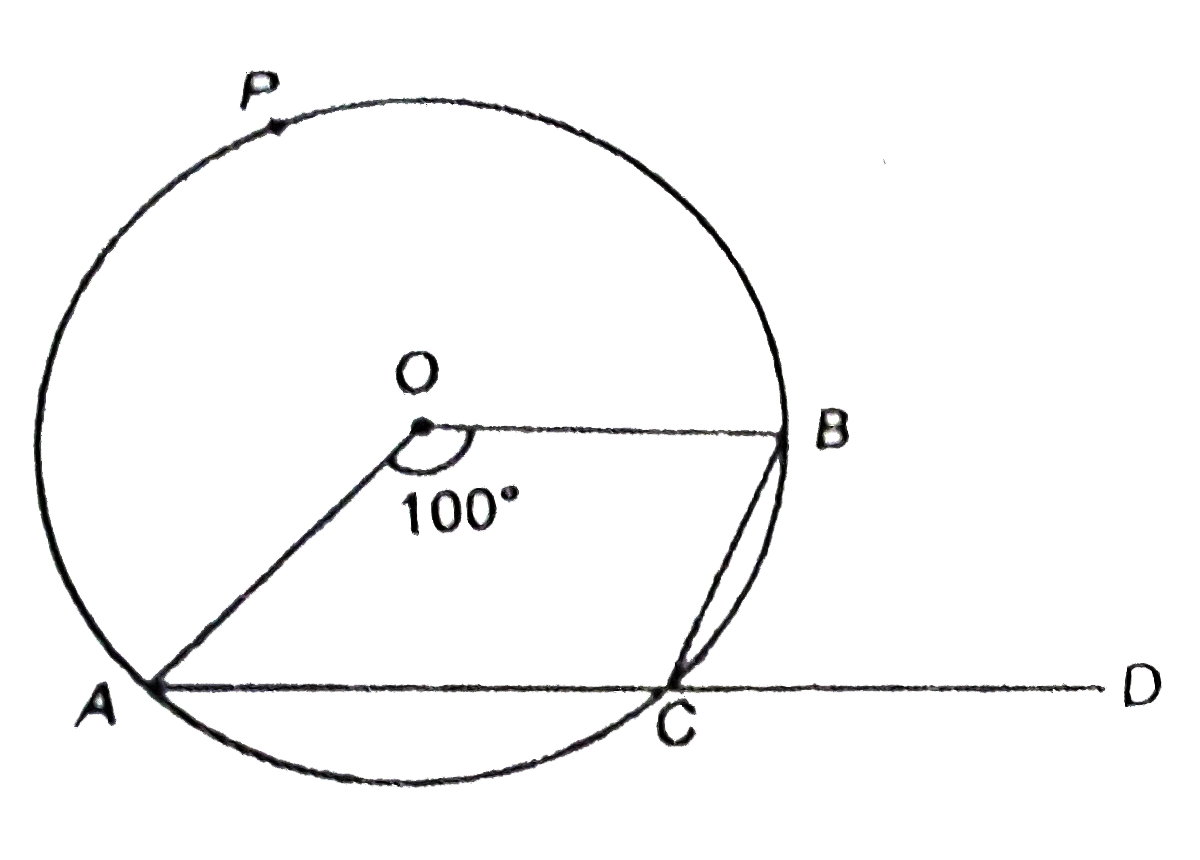
View SolutionIn the adjoining figure `O` is the centre of the circle and `angleAOB=100^(@)`. Find the value of `angleBCD`.
View SolutionIn the adjoining figure, `AC` is the diameter of the circle. If `angleBDC=115^(@)`, then find the value of `angle ACB`.
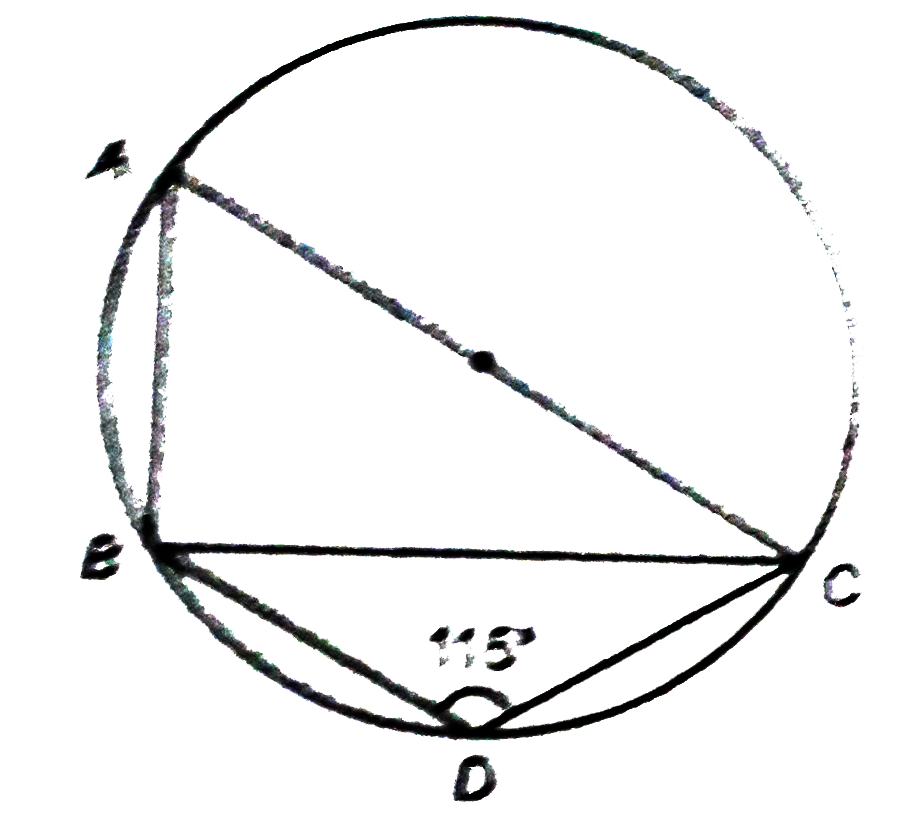
View SolutionIn the adjoining figure, `ABCD` is a cyclic quadrilateral. If `angleDBC=60^(@)` and `angleBAC=40^(@)` , then find the value of `angleBCD` .
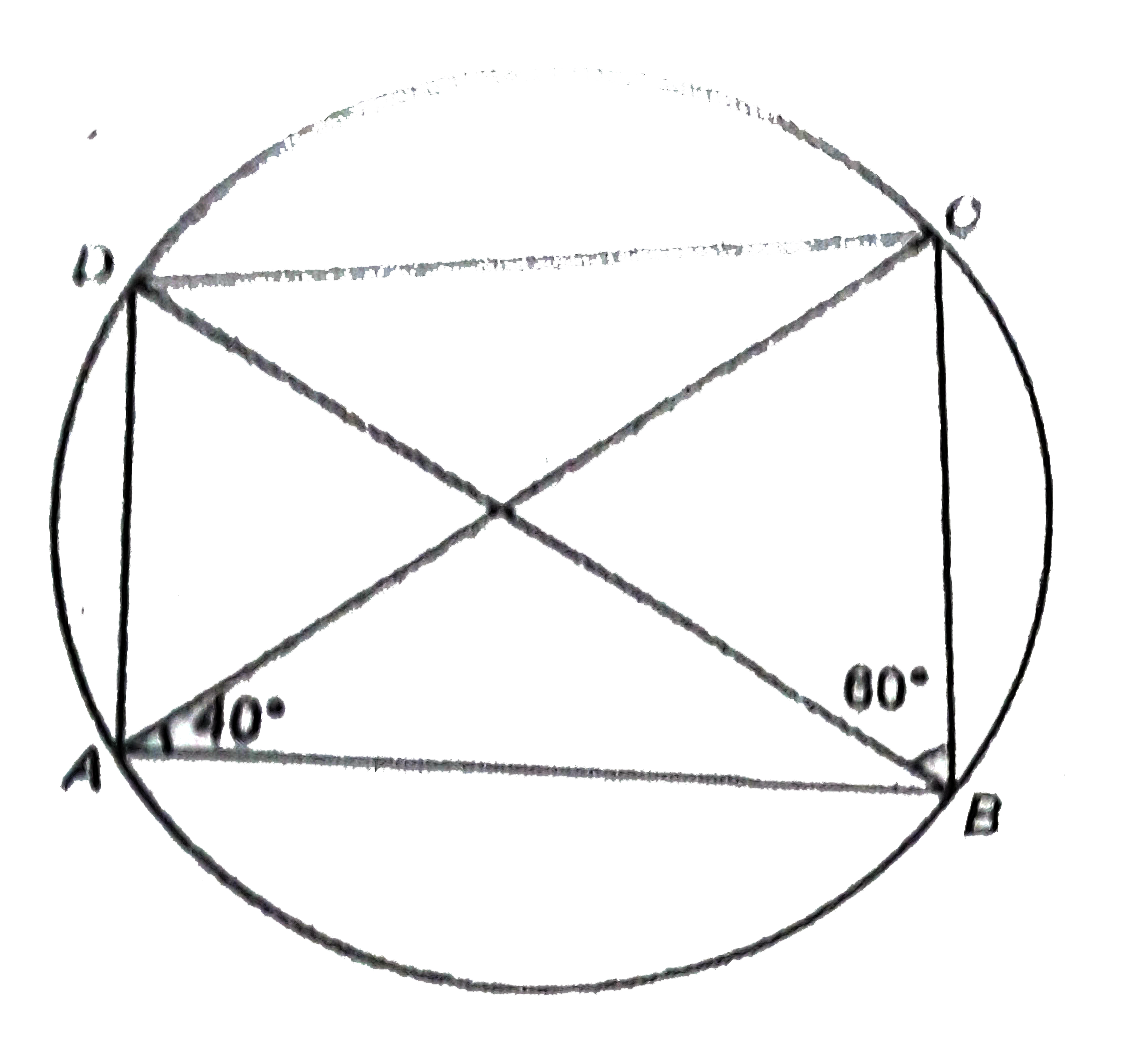
View SolutionIn the adjoining figure, `ABCD` is a cyclic quadrilateral whose side `AB` is the diameter of the circle . If `angle ADC=140^(@)` , then find the value of `angleBAC`.

View SolutionIn the adjoining figure , `O` is the center of the circle. If `angleBAD=30^(@)` , then find the values of `x,y` and `z.`
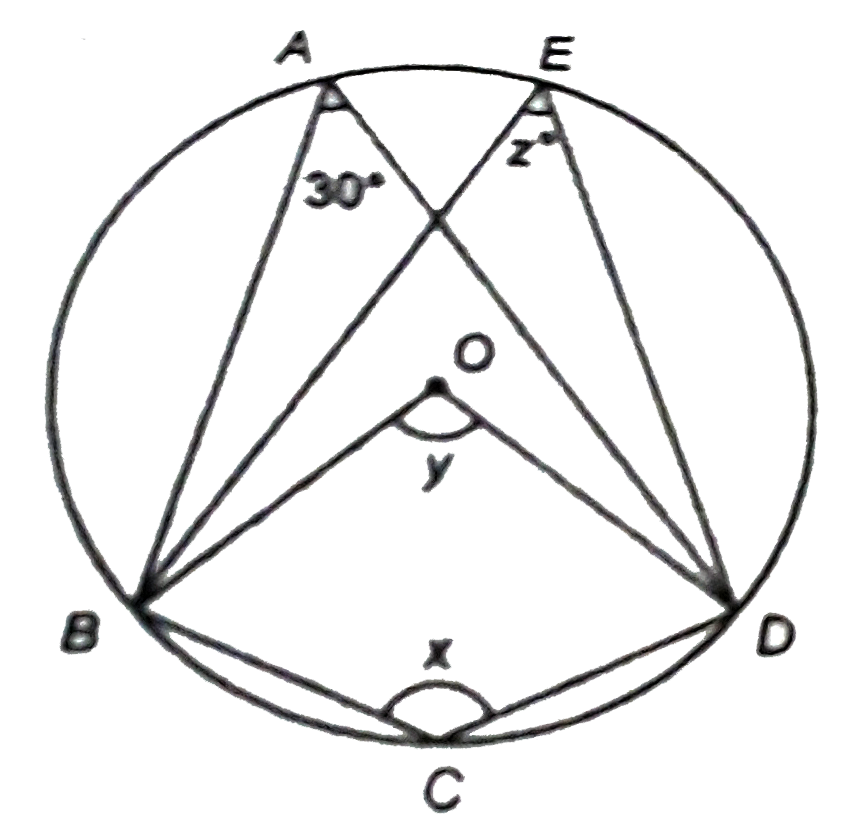
View SolutionIn a cyclic trapezium `ABCD`, side `AB` is parallel to side `DC`. Prove that :
side `AD` = side `BC`.
View SolutionIf the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
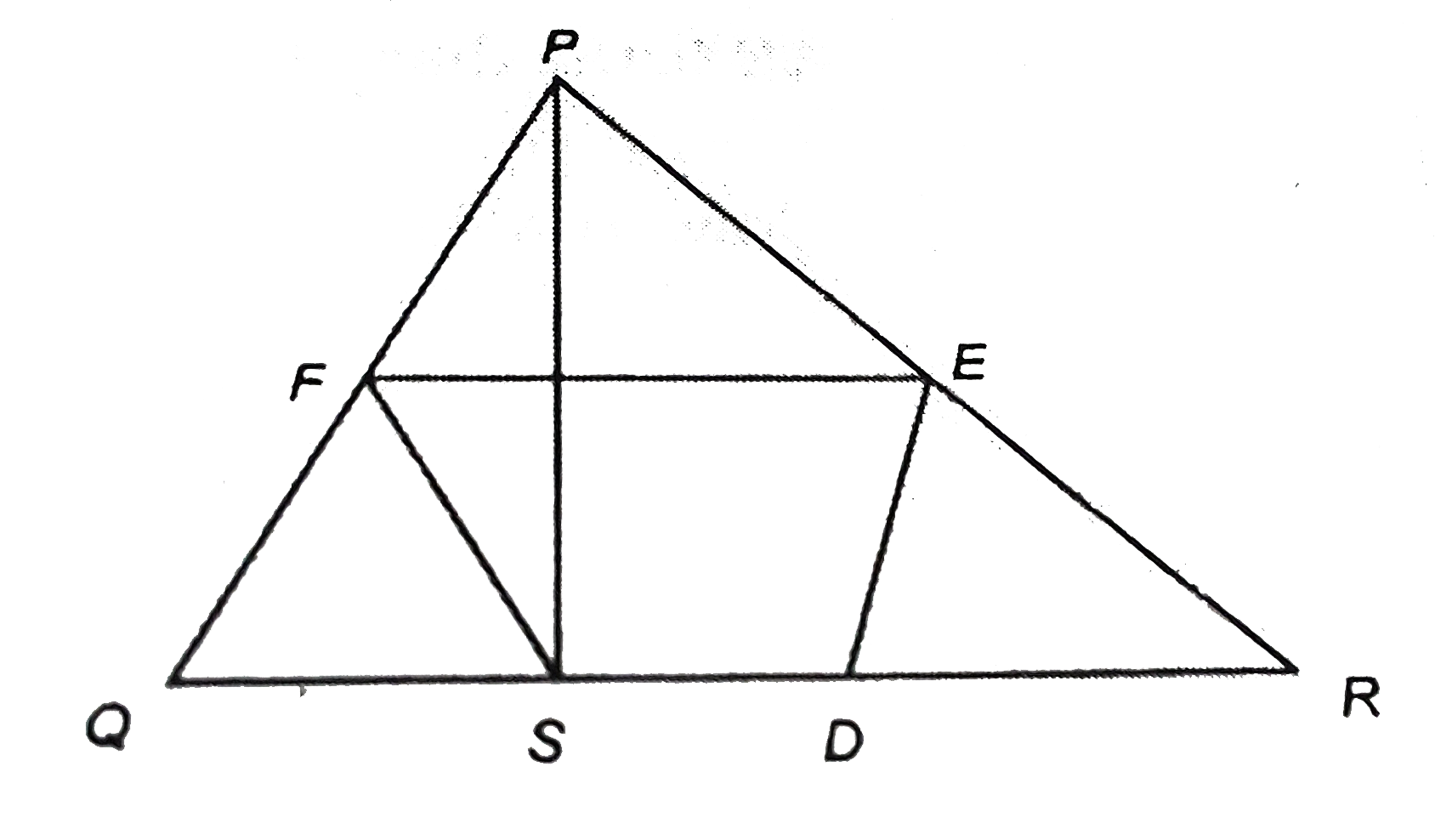
View SolutionIn the adjoining figure, `D,E` and `F` are the mid- points of the sides of `DeltaPQR` and `S` is the foot of perpendicular form `P` to side `S.`
Prove that:
(i) `FQ=FS` and `angleFQS=angle FSQ`.
(ii)` angle FQS=angleFED`.
(iii) square `FSDE` is a cyclic quadrilateral.
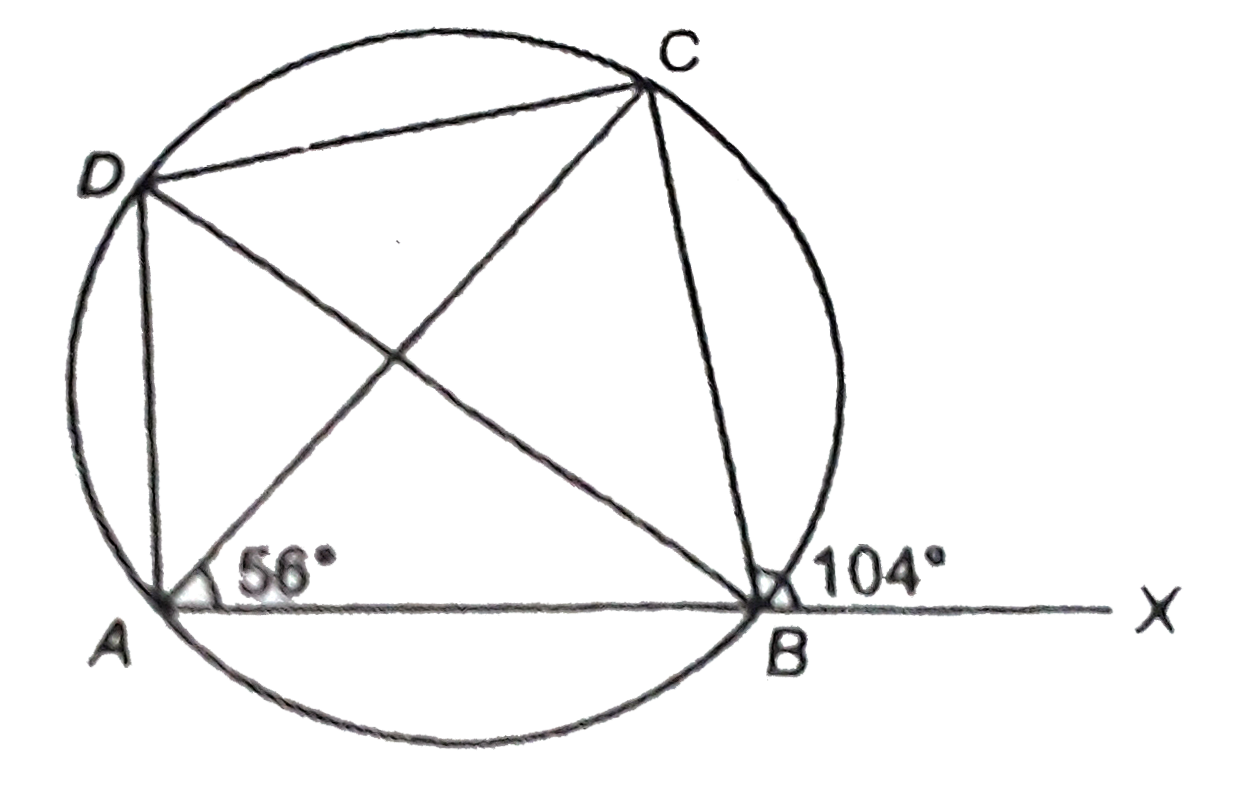
View SolutionIn the adjoining figure, `ABCD` is a cyclic quadrilateral . If `angleCBX=104^(@)` and `angleCAB=56^(@)`, then find the value of `angleADB`.
View Solution`ABCD` is a cyclic trapezium , in which `AB "||" DC`. If `angleB=75^(@)` , then find other angles.
View SolutionThe sides `AB` and `DC` of a cyclic quadrilateral `ABCD` when produced meet at `E` and the sides `DA` and `CB` when produced meet at `F.` Given `angle BEC=38^(@)`,`angle BAD=102^(@)`. Find the values of `angle AFB` and `angle ADC`.
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that `AE=AD`.
View SolutionProve that the perpendicular let fall from the vertices of a triangle to the opposite sides are concurrent.
View SolutionA circle intersects the side `AD` of a parallelogram `ABCD` at P and BC produced at Q. Prove that square `PDQC` is cyclic .
View SolutionThe line joining the foot of perpendicular drawn from a point lying on the circumcircle. Of a triangle to the sides of a triangle is a straight line.
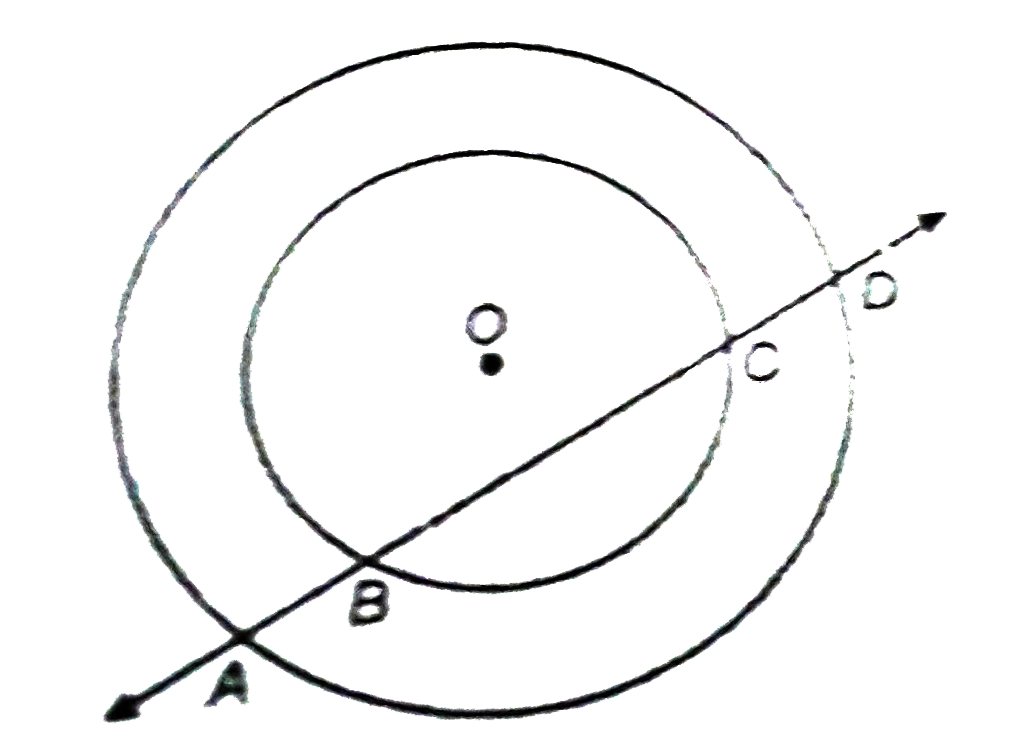
View SolutionIf a line intersects two concenteric circles (circles with the same centre) with center O at A,B,C and D, prove that AB=CD (see figure).
View SolutionThree girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip
View SolutionA circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
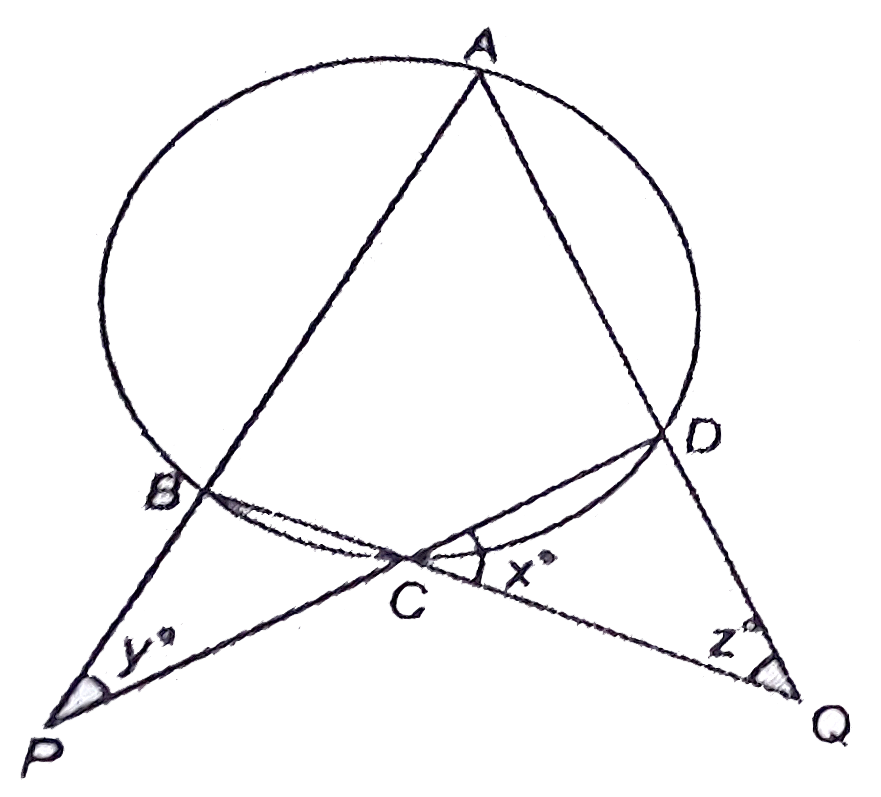
View SolutionTwo circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that `/_A C P\ =/_Q C D`.
View SolutionThe circumcentre of the triangle ABC is O . Prove that `angle OBC+angle BAC=90^@`.
View SolutionIf P, Q and R are the mid-points of the sides, BC, CA and AB of a triangle and AD is the perpendicular from A on BC, then prove that P, Q, R and D are concyclic.
View SolutionIf bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
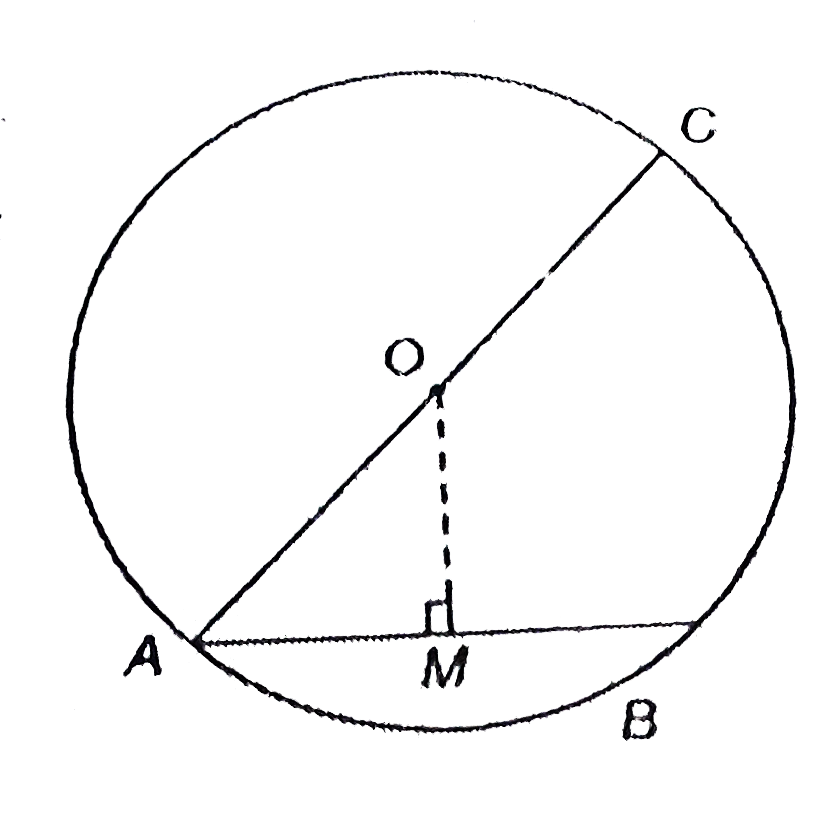
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
View SolutionA chord 16 cm long is 6 cm distant form the centre of the circle . Find the diameter of the circle.
View SolutionIn the adjoining figure, BD is the diameter of the circle which bisects the chord AC at point E. If `AC=8cm`, `BE=2cm`, then find the radius of the circle.

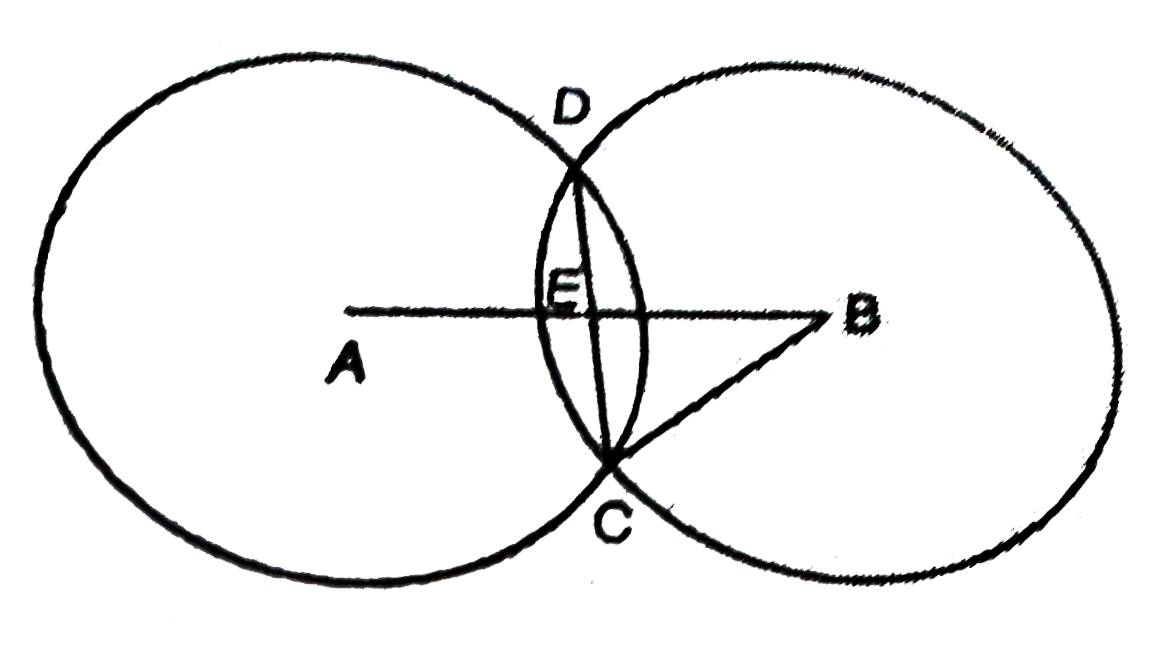
View SolutionIn the adjoining figure, A and B are the centres of two circles. If CB=17cm, EB=15cm, then find the length of common chord.
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionProve that the line joining the mid-points of two parallel chords of a circle passes through the center.
View SolutionIn an equilateral triangle prove that the centroid and the centre of the circumcircle (circumcentre) coincide.
View SolutionIn figure, `oversetfrown(AB)congoversetfrown(AC)` and O is the centre of the circle,Prove that OA is the perpendicualr bisector of BC.
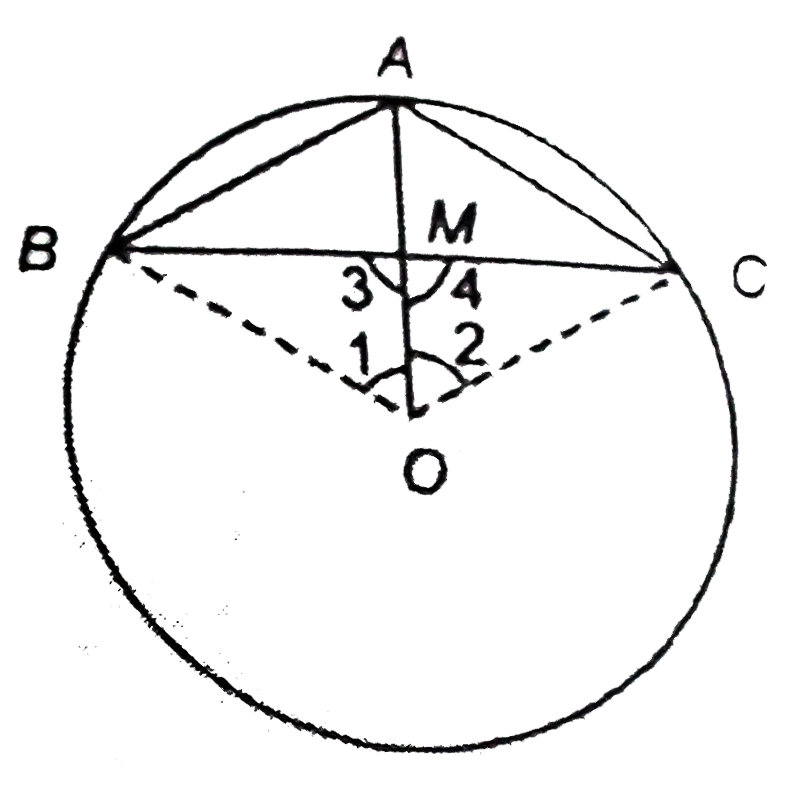
View SolutionAB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10 cm, CD=24 cm and the distance between AB and CD is 17 cm.Find the radius of the circle.
View SolutionA point P lies outside the circle with centre O. two lines PAOB and PDC are drawn on the circle from P. if PD =OD, then prove that arc `BC=3xxArcAD`.
View SolutionProve that the chords inclined on the same angle to the radius or diameter of a circle are equal in length.
View SolutionIn the figure, `O D` is perpendicular to the chord `A B` of a circle whose centre is `Odot` If `B C` is a diameter, show that `C A=2O Ddot`
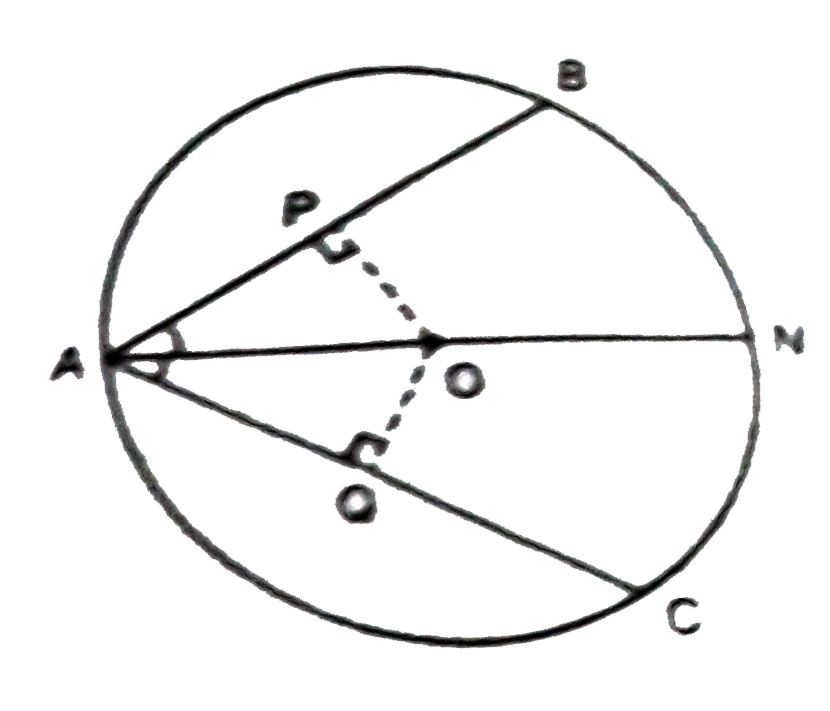
View Solution`A B\ a n d\ C D` are two parallel chords of a circle whose diameter is `A C` . Prove that `A B=C D`
View SolutionTwo circles whose centres are `O` and `O '` intersect at `Pdot` Through `P ,` a line `l` parallel to `O O '` intersecting the circles at `C\ a n d\ D` is drawn. Prove that `C D=2\ O O '`
View Solutionprove that the line joining the mid-point of two equal chords of a circle subtends equal angles with the chord.
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.

View SolutionAB is the chord of a circle with centreO. AB is produced to C, such that BC =OB, CO is joined and produced to meet the circle in D.
If `angle ACD=Y^@` and `angle AOD=x^@`, Prove that `x = 3y`.
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
View SolutionIn the figure, two circles with centres `A and B` and of radii `5cm and 3cm` touch each other intermally. If the perpendicular bisectors of segment AB meets the bigger circle in `P and Q.` Find the length of `PQ.`
View SolutionOf any two chords of a circle show that the one which is nearer to the centre is larger.
View Solution
Solved Examples questions and complete solutions for chapter CIRCLE of NAGEEN MATHS (HINGLISH) of Class 9