Complete Solutions to All Questions of chapter CIRCLE of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLE |
| Mathematics | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Equal chords of a circle subtend equal angles at the centre.
View SolutionChords of congruent circles which are equidistant from the corresponding centres, are equal.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, the chords are equal.
View SolutionOf any two chords of a circle show that one which is larger is nearer to the centre.
View SolutionIf the angles subtended by two chords of congruent circles at the corresponding centres are equal, the chords are equal.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionTwo equal chords `A B` and `C D` of a circle with centre `O` , when produced meet at a point `E ,` as shown in Figure, Prove that `B E=D E` and `A E=C Edot`
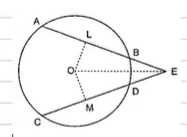
View SolutionTwo equal chords `A B` and `C D` of a circle with centre `O ,` when produced meet at a point `E ,` as shown in Figure. Prove that `B E=D E` and `A E=C Edot`
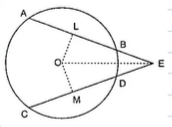
View SolutionOf any two chords of a circle show that the one which is nearer to the centre is larger.
View SolutionChords of a circle which are equidistant from the centre are equal.
View SolutionEqual chords of congruent circles are equidistant from the corresponding centres.
View SolutionThe length of two parallel chords of a circle are `6c m` and `8c mdot` If the smaller chord is at a distance of `4c m` from the centre, what is the distance of the other chord from the centre?
View SolutionEqual chords of a circle are equidistant from the centre.
View SolutionTwo circle with centres `A` and `B` intersect at `C` and `Ddot` Prove that `/_A C B=/_A D Bdot`
View SolutionProve that the line joining the mid-points of two parallel chords of a circle passes through the centre.
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionProve that the line joining the mid-points of two parallel chords of a circle passes through the centre.
View SolutionTwo circles of radil `5c m` and `3c m` intersect at two points and the distance between their centres is `4c mdot` Find the length of the common chord.
View SolutionTwo circles are drawn with sides `A B ,A C` of a triangle `A B C` as diameters. The circles intersect at a point `Ddot` Prove that `D` lies on `B Cdot`
View SolutionTwo circle intersect in `Aa n dBa n dA Ca n dA D` are respectively the diameters of the circles. Prove that `C , B , D` are collinear.
View SolutionAny angle subtended by a minor arc in the alternate segment is acute and any angle subtended by a major arc in the alternate segment is obtuse.
View SolutionThe arc of a circle subtending a right angle at any point of the circle in its alternate segment is a semi-circle.
View SolutionThe angle in a semi-circle is a right angle.
View SolutionAngle in the same segment of a circle are equal.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
View SolutionA chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the monor arc and also at a point on the major arc.
View SolutionIn Figure., `A B C` is a triangle in which `/_B A C=30^0dot` Show that `B C` is the radius of the circumcircle of ` A B C ,` whose centre is `Odot`

View SolutionTheorem:-7 If the line segment joining two points subtends equal angles at two other points lying on the same side of the line segment; the four points are concyclic. i.e lie on the same circle.
View SolutionIn Figure, `O A` and `O B` ar respectively perpendiculars to chords `C D` and `E F` of a circle whose centre is `Odot` If `O A=O B` , prove that `C E=D Fdot`

View SolutionDraw the graph of the fuction 4x+3y=12,at what pt it cut the coordinate axis
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View Solutionprove that the line joining the mid-point of two equal chords of a circle subtends equal angles with the chord.
View SolutionShow that if two chords of a circle bisect one another they must be diameters.
View SolutionIn Figure, equal chords `A B` and `C D` of a circle with centre `O ,` cut at right angles at `Edot` If `M` and `N` are mid-point of `A B` and `C D` respectively, prove that OMEN is a square.
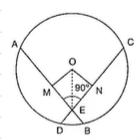
View SolutionTwo equal circles intersect in `P` and `Q` . A straight line through `P` meets the circles in `A` and `B` . Prove that `Q A=Q Bdot`
View SolutionProve that all the chords of a circle through a given point within it, the least is one which is bisected at that point.
View SolutionProve that the diameter is the greatest chord in a circle.
View SolutionBisector `A D` of `/_B A C` of ` A B C` passes through the centre `O` of the circumcircle of ` A B C` as shown in figure. Prove that `A B=A Cdot`
View SolutionIf two sides of a cyclic quadrilateral are parallel, prove that the remaining two sides are equal and the diagonals are also equal. OR A cyclic trapezium is isosceles and its diagonals are equal.
View SolutionThe quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
View SolutionIf two non-parallel sides of a trapezium are equal, it is cyclic. OR An isosceles trapezium is always cyclic.
View SolutionIf two opposite sides of a cyclic quadrilateral are equal, then the other two sides are parallel.
View SolutionThe sum of either pair of opposite angles of a cyclic quadrilateral is `180^0` OR The opposite angles of a cyclic quadrilateral are supplementary.
View SolutionIf the chord of a circle is equal to the radius of the circle, then the angle subtended by the chord at a point on the minor arc is:
View SolutionIf one side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior opposite angle.
View SolutionIf the sum of any pair of opposite angles of a quadrilateral is `180^@`; then the quadrilateral is cyclic.
View SolutionThe sum of the angles in the four segments exterior to a cyclic quadrilateral is equal to `6` right angles.
View SolutionIf the bisectors of the opposite angles `/_Pa n d/_R` of a cyclic quadrilateral `P Q R S` intersect the corresponding cicle at `Aa n dB` respectively, then `A B` is a diameter of the circle.
View SolutionIf `O` is the circumcentre of a ` A B C` and `O D_|_B C ,` prove that `/_B O D=/_Adot`
View SolutionTwo diameters of a circle intersect each other at right angles. Prove that the quadrilateral formed by joining their end-points is a square.
View Solution`A B C` and `A D C` are two right triangles with common hypotenuse `A Cdot` Prove that `/_C A D=/_C B Ddot`
View SolutionIn a circle with centre `O ,` chords `A Ba n dC D` intersect inside the circumference at `Edot` Prove that `/_A O C+/_B O D=2/_A E Cdot`
View Solution`triangle ABC` AND `triangle ADC` are two right triangles with common hypotenuse `A Cdot` Prove that `/_C A D=/_C B Ddot`
View SolutionBisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90o-1/2A` ,`90o-1/2B` and `90o-1/2C`
View SolutionProve that the circle drawn with any side of a rhombus as a diameter, posses through the point of intersection of its diagonals.
View Solution`A Ca n dB D` are chords of a circle that bisect each other. Prove that:AC and BD are diameter. ABCD is a rectangle
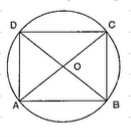
View Solution`Prove that the mid-point of the hypotenuse of a right triangle is equidistant from its vertices
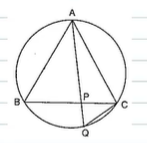
View SolutionIn Figure, `P ,` is any point on the chord `B C` of a circle such that `A B=A Pdot` Prove that `C P=C Qdot`
View SolutionTwo chords `A B` and `C D` of a circle are parallel and a line `l` is the perpendicular bisector of `A B` . Show that `l` bisects `C Ddot`
View SolutionA circular park of radius `20m` is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other.
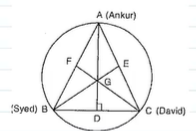
View SolutionIn an equilateral triangle, prove that the centroid and the circumcentre coincide.
View SolutionIn Figure, `l` is a line intersecting the two concentric circles, whose common centre is `O ,` at the points `A ,B ,C` and `D` . Show that `A B=C Ddot`

View SolutionIn the Figure, `O D` is perpendicular to the chord `A B` of a circle whose centre is `Odot` If `B C` is a diameter, show that `C A=2 OD`
View SolutionAB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle
View Solution`A B` and `C D` are two parallel chords of a circle such that `A B=10c m` and `C D=24c mdot` If the chords are on the opposite sides of the centre and the distance between them is `17c m ,` find the radius of the circle.
View Solution`P Q` and `R S` are two parallel chords of a circle whose centre is `O` and radius is `10c mdot` If `P Q=16c m` and `R S=12c m ,` find the distance between `P Q` and `R S ,` if they lie: on the same side of the centre `Odot` on opposite side of the centre `Odot`
View Solution`A B` and `C D` are two parallel chords of a circle whose diameter is `A C` . Prove that `A B=C Ddot`
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionProve that the line joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.
View SolutionProve that the angle in a segment greater than a semi-circle is less than a right angle.
View SolutionProve that the angle in a segment greater than a semi-circle is less than a right angle.
View Solution`A B C D` is a parallelogram. `A B` is produced to `E` so that `B E=A B` . Prove that `E D` bisects `B Cdot`
View SolutionIf two sides of a cyclic quadrilateral are parallel, prove that the remaining two sides are equal and the diagonals are also equal.(in figure) OR A cyclic trapezium is isosceles and its diagonals are equal.

View SolutionProve that the circle drawn with any side of a rhombus as a diameter,passes through the point of intersection of its diagonal
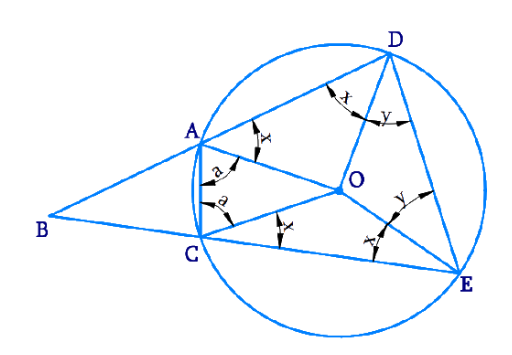
View SolutionLet the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
View SolutionIn any triangle ABC, if the angle bisector of `/_A`and perpendicular bisector of BCintersect, prove that they intersect on the circumcircle of the triangle ABC
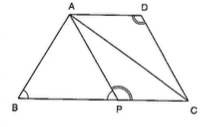
View Solution`P` is a point on the side `B C` of a triangle `A B C` such that `A B=A Pdot` Through `Aa n dC ,` lines are drawn parallel to `B Ca n dP A ,` respectively, so as to intersect at `D` as shown in Figure. Show that `A B C D` is a cyclic quadrilateral.
View Solution`A B C D` is a cyclic quadrilateral whose diagonals `A Ca n dB D` intersect at `P` . If `A B=D C ,` Prove that : ` P A BcongP D C` `P A=P Da n dP C=P B` `A D B C`
View Solution(Converse of Theorem 3) The line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.
View Solution.The equation of the circle passing through three non-collinear points P(`x_1,y_1`) Q(`x_2,y_2`) and R(`x_3,y_3`) is
View SolutionTwo chords `A B` and `A C` of a circle are equal. Prove that the centre of the circle lies on the angle bisector of `/_B A Cdot`
View SolutionIf two chords `A B` and `A C` of a circle with centre `O` are such that the centre `O` lies on the bisector of `/_B A C ,` prove that `A B=A C` , i.e. the chords are equal.
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionIf two chord of a circle (or of congruent circles) are equal, then their corresponding arcs. (minor, major or semi-circular) are congruent.
View SolutionThe perpendicular from the centre of a circle to a chord bisects the chord.
View SolutionIf two circles intersect in two points, prove that the line through the centres is the perpendicular bisector of the common chord.
View SolutionFind the length of the chord which is at 12 cm distance from center and radius of circle is 13cm.
View SolutionIn an isosceles triangle `A B C` with `A B=A C ,` a circle passing through `B` and `C` intersects the sides `A Ba n dA C` at`Da n dE` respectively. Prove that `D E C Bdot`
View Solution`P Qa n dR S` are two parallel chords of a circle and lines `R Pa n dS Q` intersect each other at `O` as shown in Figure. Prove that `O P=O Qdot`

View Solution`A B C` is an isosceles triangle in which `A B=A Cdot` If `Da n dE` are the mid-points of `A Ba n dA C` respectively, prove that the points `B ,C ,Da n dE` are concylic.
View Solution`Da n dE` are points on equal sides `A Ba n dA C` of an isosceles triangle `A B C` such that `A D=A E` . Prove that `B ,C ,D ,E` are concylic.
View Solution`D\ a n d\ E` are, respectively, the points on equal sides `A B\ a n d\ A C` of an isosceles triangle `A B C` such that `B ,\ C ,\ E ,\ a n d\ D` are concyclic as shown in Figure. If `O` is the point of intersection of `C D\ a n d\ B E ,` prove that `A O` is the bisector of line segment `D E`
View Solution`A B C D` is a cyclic quadrilateral. `A Ba n dD C` are produced to meet in `Edot` Prove that `E B C-E D Adot`
View SolutionIn Figure, `P Q R S` is a cyclic quadrilateral. Find the measure of each of its angles.
View SolutionProve that any cyclic parallelogram is a rectangle.
View Solution`A Ca n dB D` are chords of a circle which bisect each other. Prove that (i) `A Ca n dB D` are diameters (ii) `A B C D` is a rectangle.
View Solution`A B C D` is a parallelogram. The circle through `A ,B and C` intersects `C D` produced at `E ,` prove that `A E=A Ddot`
View SolutionFill in the blanks: All point lying inside/outside a circle are called ... points/ ... points. Circle having the same centre and different radii are called ... circles. A point whose distance from the centre of a circle is greater than its radius lies in .... of the circle. A continuous piece of a circle is .... of the circle. The longest chord of a circle is a ......of the circle. An arc is a ......... when its ends are the ends of a diameter. Segment of a circle is the region between an arc and ... of the circle. A circle divides the plane, on which it lies, in .... parts.
View Solution
All Questions questions and complete solutions for chapter CIRCLE of RD SHARMA MATHS (HINGLISH) of Class 9